Arcsin-Verteilung

Arcsin-Verteilung
Dichtefunktion
Verteilungsfunktion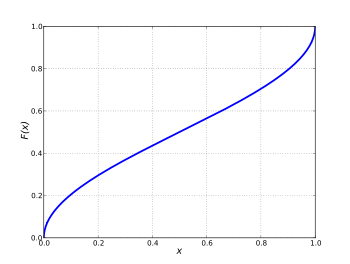
Parameter	keine
Träger	${\displaystyle x\in [0,1]}$
Dichtefunktion	${\displaystyle {\frac {1}{\pi {\sqrt {x(1-x)}}}}}$
Verteilungsfunktion	${\displaystyle {\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)}$
Erwartungswert	${\displaystyle {\frac {1}{2}}}$
Median	${\displaystyle {\frac {1}{2}}}$
Modus	${\displaystyle \{0,1\}}$
Varianz	${\displaystyle {\frac {1}{8}}}$
Schiefe	${\displaystyle 0}$

Die Arcsin-Verteilung, auch Arkussinus-Verteilung genannt, ist eine univariate Wahrscheinlichkeitsverteilung. Sie ist ein Spezialfall der Beta-Verteilung mit den Parametern ${\displaystyle p=q={\tfrac {1}{2}}}$ und spielt eine wichtige Rolle in der Theorie der brownschen Bewegung.

Definition

Die Arcsin-Verteilung ist eine Wahrscheinlichkeitsverteilung auf ${\displaystyle [0,1]}$. Sie ist definiert durch ihre Verteilungsfunktion

${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right),\ \ \ x\in [0,1]}$

und ihre Wahrscheinlichkeitsdichtefunktion

${\displaystyle f(x)={\begin{cases}{\frac {1}{\pi {\sqrt {x(1-x)}}}}&{\text{wenn}}\;x\in (0,1)\\0&{\text{wenn}}\;x\in \{0,1\}\\\end{cases}}}$.

Eigenschaften

Es sei ${\displaystyle X}$ eine arcsin-verteilte Zufallsvariable.

Erwartungswert und Varianz

Der Erwartungswert ergibt sich zu

${\displaystyle \operatorname {E} (X)={\frac {1}{2}}}$

und die Varianz zu

${\displaystyle \operatorname {Var} (X)={\frac {1}{8}}}$.

Symmetrie

Die Arcsin-Verteilung ist symmetrisch um 0,5.

Arcsin-Gesetze

Es gibt eine Vielzahl von Arcsin-Gesetzen. Veröffentlichungen dazu stammen unter anderem von Paul Lévy, Paul Erdős, Mark Kac und Erik Sparre Andersen. Nach ihnen sind die Arcsin-Gesetze zum Teil benannt.

Die folgenden Arcsin-Gesetze treffen Aussagen über die Dauer, wie lange sich ein stochastischer Prozess im positiven Bereich aufhält. Es können stattdessen auch die Abbildungen:

• frühester Zeitpunkt eines Maximums und
• dem Zeitpunkt, wann zum letzten Mal der Ursprung gekreuzt wird

betrachtet werden, wobei dann gegebenenfalls weitere Annahmen getroffen werden müssen.

Arcsin-Gesetz von Paul Lévy

Die Zeitlängen, die ein eindimensionaler Standard-Wiener-Prozess ${\displaystyle (W_{t})_{t\in [0,1]}}$ positiv ist, sind arcsin-verteilt. Das heißt für

${\displaystyle U:=\lambda (\{t\in [0,1]\mid W_{t}>0\}),\ \ \ x\in [0,1]}$,

gilt

${\displaystyle P(U\leq x)=F(x),\ \ \ x\in [0,1]}$,

wobei ${\displaystyle \lambda }$ das eindimensionale Lebesgue-Maß bezeichnet.^[1][2]

Arcsin-Gesetz von Paul Erdős und Mark Kac

Sei ${\displaystyle (X_{i})_{i\in \mathbb {N} }}$ eine Folge von eindimensionalen, unabhängigen und identisch verteilten Zufallsvariablen. Weiter wird angenommen, dass sie Erwartungswert 0 und Varianz 1 haben. Die fortlaufenden Anzahlen der Summen

${\displaystyle S_{k}:=X_{1}+\dotsb +X_{k},\ \ \ k\in \mathbb {N} }$,

die positiv sind, sind definiert durch

${\displaystyle N_{n}:=|\{k\in \{1,\dotsc ,n\}\mid S_{k}>0\}|,\ \ \ n\in \mathbb {N} }$.

Dann gilt die folgende Konvergenz in Verteilung

${\displaystyle \lim _{n\rightarrow \infty }P\left({\frac {N_{n}}{n}}\leq x\right)=F(x),\ \ \ x\in [0,1]}$.^[3]

Die Annahmen können variiert werden, sofern der Zentrale Grenzwertsatz weiterhin für ${\displaystyle (X_{i})_{i\in \mathbb {N} }}$ gilt.

Arcsin-Gesetz von Erik Sparre Andersen

Sei ${\displaystyle (X_{i})_{i\in \mathbb {N} }}$ eine Folge von Zufallsvariablen. Zu jeder Auswahl von endlich vielen Zufallsvariablen existieren die gemeinsamen Dichten und diese sind invariant bezüglich s-Permutationen. Eine s-Permutation besteht aus der Kompositionen einer Permutation und Vorzeichenwechsel in beliebigen Koordinaten. Dann gilt analog zum Arcsin-Gesetz von Erdős und Kac für die Summen ${\displaystyle S_{k},\ k\in \mathbb {N} ,}$ und die die Anzahl von positiven Zufallsvariablen ${\displaystyle N_{n},n\in \mathbb {N} ,}$ die folgende Konvergenz in Verteilung

${\displaystyle \lim _{n\rightarrow \infty }P\left({\frac {N_{n}}{n}}\leq x\right)=F(x),\ \ \ x\in [0,1]}$.^[4]

Diskrete Arcsin-Verteilung

In der Fluktuationstheorie konnte Erik Sparre Andersen zeigen, dass die sogenannte diskrete Arcsin-Verteilung von Bedeutung ist. Diese ist für jeden Parameter ${\displaystyle n\in \mathbb {N} \cup \{0\}}$ durch ihre Wahrscheinlichkeitsfunktion

${\displaystyle g_{n}(m)=(-1)^{n}{\binom {-{\frac {1}{2}}}{m}}{\binom {-{\frac {1}{2}}}{n-m}},\ \ \ m\leq n}$

und ihre Verteilungsfunktion

${\displaystyle G_{n}(x)=\sum \limits _{m=0}^{\lfloor x\rfloor }(-1)^{n}{\binom {-{\frac {1}{2}}}{m}}{\binom {-{\frac {1}{2}}}{n-m}},\ \ \ x\in [0,n]}$

definiert.

Der Name ist durch ihr Konvergenzverhalten zur Arcsin-Verteilung begründet, so gilt die gleichmäßige Konvergenz

${\displaystyle \lim _{n\rightarrow \infty }\sup _{x\in [0,1]}\mid G_{n}(n\cdot x)-F(x)\mid =0}$.

Erik Sparre Andersen zeigte die entsprechende Konvergenz in Verteilung im gleichen Zug mit dem vorigen Arcsin-Gesetz.

Literatur

• William Feller: An introduction to probability theory and its applications. Band 2. Wiley, 1971. 
• Konrad Jacobs: Discrete Stochastics. Birkhäuser, Basel 2012, ISBN 3-0348-8645-4. 

Fußnoten

1. ↑ Bauer, Heinz: Wahrscheinlichkeitstheorie. de Gruyter, 2002, S. 491–492. 
2. ↑ Paul Lévy: Sur certains processus stochastiques homogènes, Compositio Mathematica. Band 7, 1939, S. 283–339. 
3. ↑ Paul Erdős, Mark Kac: On the number of positive sums of independent random variables. In: Bull. Amer. Math. Soc. Band 53, Nr. 10, 1947, S. 1011–1020. 
4. ↑ Erik Sparre Andersen: On the Number of Positive Sums of Random Variables. In: Scandinavian Actuarial Journal. Band 1949, Nr. 1, 1949, S. 27–36, doi:10.1080/03461238.1949.10419756.