Differentialrechnung
Die Differential- oder Differenzialrechnung ist ein wesentlicher Bestandteil der Analysis und damit ein Gebiet der Mathematik. Zentrales Thema der Differentialrechnung ist die Berechnung lokaler Veränderungen von Funktionen. Während eine stetige Funktion ihren Eingabewerten kontinuierlich gewisse Ausgangswerte zuordnet, wird durch die Differentialrechnung ermittelt, wie stark sich die Ausgabewerte nach sehr kleinen Veränderungen der Eingabewerte ändern. Sie ist eng verwandt mit der Integralrechnung, mit der sie gemeinsam unter der Bezeichnung Infinitesimalrechnung zusammengefasst wird.
Die Ableitung einer Funktion dient der Darstellung lokaler Veränderungen einer Funktion und ist gleichzeitig Grundbegriff der Differentialrechnung. Anstatt von der Ableitung spricht man auch vom Differentialquotienten, dessen geometrische Entsprechung die Tangentensteigung ist. Die Ableitung ist nach der Vorstellung von Leibniz der Proportionalitätsfaktor zwischen infinitesimalen Änderungen des Eingabewertes und den daraus resultierenden, ebenfalls infinitesimalen Änderungen des Funktionswertes. Eine Funktion wird als differenzierbar bezeichnet, wenn ein solcher Proportionalitätsfaktor existiert. Äquivalent wird die Ableitung in einem Punkt als die Steigung derjenigen linearen Funktion definiert, die unter allen linearen Funktionen die Änderung der Funktion am betrachteten Punkt lokal am besten approximiert. Entsprechend wird mit der Ableitung in dem Punkt eine lineare Näherung der Funktion gewonnen. Die Linearisierung einer möglicherweise komplizierten Funktion hat den Vorteil, dass eine einfacher behandelbare Funktion entsteht als die ursprüngliche Funktion oder überhaupt erst eine Handhabbarkeit.
In vielen Fällen ist die Differentialrechnung ein unverzichtbares Hilfsmittel zur Bildung mathematischer Modelle, die die Wirklichkeit möglichst genau abbilden sollen, sowie zu deren nachfolgender Analyse.
- Das Verhalten von Bauelementen mit nicht-linearer Kennlinie wird bei kleinen Signaländerungen in der Umgebung eines Bezugspunktes durch ihr Kleinsignalverhalten beschrieben; dieses basiert auf dem Verlauf der Tangente an die Kennlinie im Bezugspunkt.
- Die Ableitung nach der Zeit ist im untersuchten Sachverhalt die momentane Änderungsrate. So ist beispielsweise die Ableitung der Orts- beziehungsweise Weg-Zeit-Funktion eines Teilchens nach der Zeit seine Momentangeschwindigkeit, und die Ableitung der Momentangeschwindigkeit nach der Zeit liefert die momentane Beschleunigung.
- In den Wirtschaftswissenschaften spricht man auch häufig von Grenzraten anstelle der Ableitung, zum Beispiel Grenzkosten oder Grenzproduktivität eines Produktionsfaktors.
In der Sprache der Geometrie ist die Ableitung eine verallgemeinerte Steigung. Der geometrische Begriff Steigung ist ursprünglich nur für lineare Funktionen definiert, deren Funktionsgraph eine Gerade ist. Die Ableitung einer beliebigen Funktion an einer Stelle kann man als die Steigung der Tangente im Punkt des Graphen von definieren.
In der Sprache der Arithmetik schreibt man für die Ableitung einer Funktion an der Stelle . Sie gibt an, um welchen Faktor von sich ungefähr ändert, wenn sich um einen „kleinen“ Betrag ändert. Für die exakte Formulierung dieses Sachverhalts wird der Begriff Grenzwert oder Limes verwendet.
Einführung
Heranführung anhand eines Beispiels
Fährt ein Auto auf einer Straße, so kann anhand dieses Sachverhalts eine Tabelle erstellt werden, in der zu jedem Zeitpunkt die Strecke, die seit dem Beginn der Aufzeichnung zurückgelegt wurde, eingetragen wird. In der Praxis ist es zweckmäßig, eine solche Tabelle nicht zu engmaschig zu führen, d. h. zum Beispiel in einem Zeitraum von 1 Minute nur alle 3 Sekunden einen neuen Eintrag zu machen, was lediglich 20 Messungen erfordern würde. Jedoch kann eine solche Tabelle theoretisch beliebig engmaschig gestaltet werden, wenn jeder Zeitpunkt berücksichtigt werden soll. Dabei gehen die vormals diskreten, also mit einem Abstand behafteten Daten, in ein Kontinuum über. Die Gegenwart wird dann als Zeitpunkt, d. h. als ein unendlich kurzer Zeitabschnitt, interpretiert. Gleichzeitig hat das Auto aber zu jedem Zeitpunkt eine theoretisch bekannte Strecke zurückgelegt, und wenn es nicht bis zum Stillstand abbremst oder gar zurück fährt, wird die Strecke kontinuierlich ansteigen, also zu keinem Zeitpunkt dieselbe sein wie zu einem anderen.
-
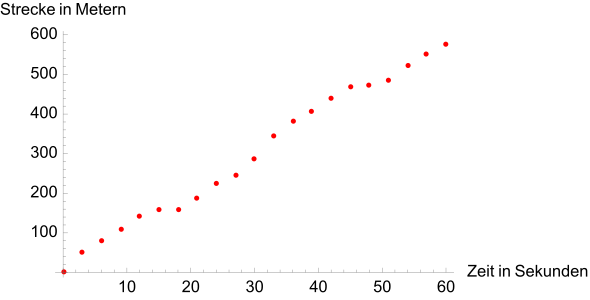
Exemplarische Darstellung einer Tabelle, alle 3 Sekunden wird eine neue Messung eingetragen. Unter solchen Voraussetzungen können lediglich durchschnittliche Geschwindigkeiten in den Zeiträumen 0 bis 3, 3 bis 6 usw. Sekunden berechnet werden. Da die zurückgelegte Strecke stets zunimmt, scheint der Wagen nur vorwärts zu fahren. -
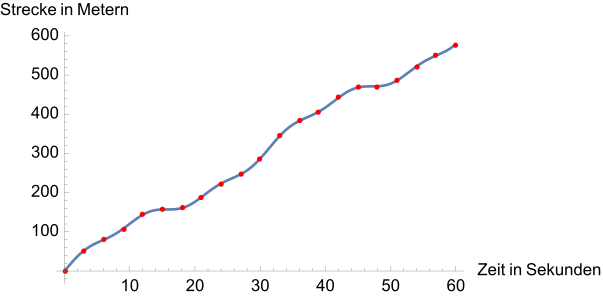
Übergang zu einer beliebig engmaschigen Tabelle, die nach Eintragung aller Punkte die Gestalt einer Kurve annimmt. Jedem Zeitpunkt zwischen 0 und 60 Sekunden wird ein Punkt auf der Kurve zugeordnet. Regionen, innerhalb derer die Kurve steiler nach oben verläuft, entsprechen Zeitabschnitten, in denen eine größere Strecke pro Zeitspanne zurückgelegt wird. In Regionen mit nahezu gleich bleibender Strecke, zum Beispiel im Bereich 15–20 Sekunden, fährt das Auto langsam und die Kurve verläuft flach.
Die Motivation hinter dem Begriff der Ableitung einer Weg-Zeit-Kurve oder -Funktion ist, dass nun angegeben werden kann, wie schnell sich das Auto zu einem momentanen Zeitpunkt bewegt. Aus einem Weg-Zeit-Verlauf soll also der passende Geschwindigkeit-Zeit-Verlauf abgeleitet werden. Hintergrund ist, dass die Geschwindigkeit ein Maß dafür ist, wie stark sich die zurückgelegte Strecke im Laufe der Zeit ändert. Bei einer hohen Geschwindigkeit ist ein starker Anstieg in der Kurve zu sehen, während eine niedrige Geschwindigkeit zu wenig Veränderung führt. Da jedem Messpunkt auch eine Strecke zugeordnet wurde, sollte eine solche Analyse grundsätzlich möglich sein, denn mit dem Wissen über die zurückgelegte Strecke innerhalb einem Zeitintervall gilt für die Geschwindigkeit
Sind also und zwei unterschiedliche Zeitpunkte, so lautet „die Geschwindigkeit“ des Autos im Zeitintervall zwischen diesen
Die Differenzen in Zähler und Nenner müssen gebildet werden, da man sich nur für die innerhalb eines bestimmten Zeitintervalls zurückgelegte Strecke interessiert. Dennoch liefert dieser Ansatz kein vollständiges Bild, da zunächst nur Geschwindigkeiten für Zeitintervalle mit auseinander liegendem Anfangs- und Endpunkt gemessen wurden. Eine momentane Geschwindigkeit, vergleichbar mit einem Blitzerfoto, hingegen bezöge sich auf ein unendlich kurzes Zeitintervall. Dementsprechend ist der oben stehende Begriff „Geschwindigkeit“ durch „durchschnittliche Geschwindigkeit“ zu präzisieren. Auch wenn mit echten Zeitintervallen, also diskreten Daten, gearbeitet wird, vereinfacht sich das Modell insofern, als für ein Auto innerhalb der betrachteten Intervalle keine schlagartige Ortsänderung und keine schlagartige Geschwindigkeitsänderung möglich ist. (Auch eine Vollbremsung benötigt Zeit, und zwar länger als die Zeit, in der die Reifen quietschen.) Damit ist auch in der Zeichnung der stillschweigend durchgehend eingetragene Kurvenzug ohne Sprung und ohne Knick gerechtfertigt.

Soll hingegen zu einem „perfekt passenden“ Geschwindigkeit-Zeit-Verlauf übergegangen werden, so muss der Terminus „durchschnittliche Geschwindigkeit in einem Zeitintervall“ durch „Geschwindigkeit zu einem Zeitpunkt“ ersetzt werden. Dazu muss zunächst ein Zeitpunkt gewählt werden. Die Idee ist nun, „ausgedehnte Zeitintervalle“ in einem Grenzwertprozess gegen ein unendlich kurzes Zeitintervall laufen zu lassen und zu studieren, was mit den betroffenen durchschnittlichen Geschwindigkeiten passiert. Obwohl der Nenner dabei gegen 0 strebt, ist dies anschaulich kein Problem, da sich das Auto in kürzer werdenden Zeitabschnitten bei stetigem Verlauf immer weniger weit bewegen kann, womit sich Zähler und Nenner gleichzeitig verkleinern, und im Grenzprozess ein unbestimmter Term „“ entsteht. Dieser kann unter Umständen als Grenzwert Sinn ergeben, beispielsweise drücken
exakt dieselben Geschwindigkeiten aus. Nun gibt es zwei Möglichkeiten beim Studium der Geschwindigkeiten. Entweder, sie lassen in dem betrachteten Grenzwertprozess keine Tendenz erkennen, sich einem bestimmten endlichen Wert anzunähern. In diesem Fall kann der Bewegung des Autos keine zum Zeitpunkt gültige Geschwindigkeit zugeordnet werden, d. h., der Term „“ hat hier keinen eindeutigen Sinn. Gibt es hingegen eine zunehmende Stabilisierung in Richtung auf einen festen Wert, so existiert der Grenzwert
und drückt die exakt im Zeitpunkt bestehende Geschwindigkeit aus. Der unbestimmte Term „“ nimmt in diesem Fall einen eindeutigen Wert an. Die dabei entstehende Momentangeschwindigkeit wird auch als Ableitung von an der Stelle bezeichnet; für diese wird häufig das Symbol benutzt. Mit dem Grenzwert wird die Momentangeschwindigkeit zu einem beliebigen Zeitpunkt definiert als
Prinzip der Differentialrechnung

Das Beispiel des letzten Abschnitts ist dann besonders einfach, wenn die Zunahme der zurückgelegten Strecke mit der Zeit gleichförmig, also linear verläuft. Dann liegt speziell eine Proportionalität zwischen der Veränderung der Strecke und der Veränderung der Zeit vor. Die relative Veränderung der Strecke, also ihre Zunahme im Verhältnis zur Zunahme der Zeit, ist bei dieser Bewegung immer gleichbleibend. Die mittlere Geschwindigkeit ist zu jedem Zeitpunkt auch die momentane Geschwindigkeit. Beispielsweise legt das Auto zwischen 0 und 1 Sekunden eine gleich lange Strecke zurück wie zwischen 9 und 10 Sekunden und die zehnfache Strecke zwischen 0 und 10 Sekunden. Als Proportionalitätsfaktor über den ganzen Weg gilt die konstante Geschwindigkeit , wobei sie im nebenstehenden Bild beträgt. Die zwischen beliebig weit auseinanderliegenden Zeitpunkten und zurückgelegte Strecke beträgt
- .
Allgemein bewegt sich das Auto in der Zeitspanne um die Strecke vorwärts. Speziell bei ergibt sich ein Wegstück .
Falls der Startwert bei nicht sondern beträgt, ändert dies nichts, da sich in der Beziehung die Konstante durch die Differenzbildung aus stets heraussubtrahiert. Auch anschaulich ist dies bekannt: Die Startposition des Autos ist unerheblich für seine Geschwindigkeit.
Werden statt der Variablen und allgemein die Variablen und betrachtet, so lässt sich also festhalten:
- Lineare Funktionen: Bei Linearität hat die betrachtete Funktion die Gestalt . (Für eine lineare Funktion ist nicht notwendig eine Ursprungsgerade erforderlich!) Als Ableitung gilt hieran die relative Veränderung, mit einem anderen Wort der Differenzenquotient . Sie hat in jedem Punkt denselben Wert . Die Ableitung lässt sich aus dem Ausdruck direkt ablesen. Insbesondere hat jede konstante Funktion die Ableitung , da sich mit einer Änderung des Eingabewertes nichts am Ausgabewert ändert.
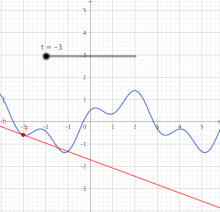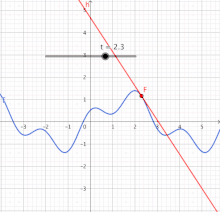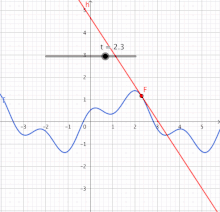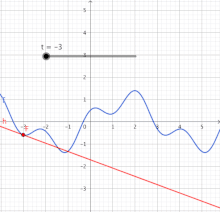
Schwieriger wird es, wenn eine Bewegung nicht gleichförmig verläuft. Dann ist das Diagramm der Zeit-Strecken-Funktion nicht geradlinig. Für derartige Verläufe muss der Ableitungsbegriff erweitert werden. Denn es gibt keinen Proportionalitätsfaktor, der überall die lokale relative Veränderung ausdrückt. Als einzig mögliche Strategie ist die Gewinnung einer linearen Näherung für die nicht-lineare Funktion gefunden worden, zumindest an einer interessierenden Stelle. (Im nächsten Bild ist das die Stelle .) Damit wird das Problem auf eine wenigstens an dieser Stelle lineare Funktion zurückgeführt. Die Methode der Linearisierung ist die Grundlage für den eigentlichen Kalkül der Differentialrechnung. Sie ist in der Analysis von sehr großer Bedeutung, da sie dabei hilft, komplizierte Vorgänge lokal auf leichter verständliche Vorgänge, nämlich lineare Vorgänge, zu reduzieren.[1]
| 0,5 | 0,9 | 0,99 | 0,999 | 1 | 1,001 | 1,01 | 1,1 | 1,5 | 2 | |
| 0,25 | 0,81 | 0,9801 | 0,998001 | 1 | 1,002001 | 1,0201 | 1,21 | 2,25 | 4 | |
| 0 | 0,8 | 0,98 | 0,998 | 1 | 1,002 | 1,02 | 1,2 | 2 | 3 | |
| −0,25 | −0,01 | −0,0001 | −0,000001 | 0 | −0,000001 | −0,0001 | −0,01 | −0,25 | −1 | |
| 50 % | 10 % | 1 % | 0,1 % | 0,1 % | 1 % | 10 % | 50 % | 100 % |
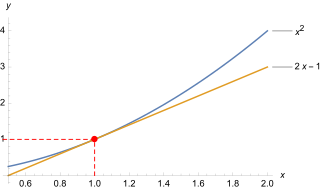
Die Strategie soll exemplarisch an der nicht-linearen Funktion erläutert werden.[2] Die Tabelle zeigt Werte für diese Funktion und für ihre Näherungsfunktion an der Stelle , das ist . Darunter enthält die Tabelle die Abweichung der Näherung von der ursprünglichen Funktion. (Die Werte sind negativ, weil in diesem Fall die Gerade immer unter der Kurve liegt – außer im Berührpunkt.) In der letzten Zeile steht der Betrag der relativen Abweichung, das ist die Abweichung bezogen auf die Entfernung der Stelle vom Berührpunkt bei . Diese kann am Berührpunkt nicht berechnet werden. Aber die Werte in der Umgebung zeigen, wie sich die relative Abweichung einem Grenzwert nähert, hier dem Wert null. Diese Null bedeutet: Selbst wenn sich ein wenig (infinitesimal) vom Berührpunkt entfernt, entsteht noch kein Unterschied zwischen und .
Die lineare Funktion ahmt das Verhalten von nahe der Stelle gut nach (besser als jede andere lineare Funktion). Die relative Veränderung hat überall den Wert . Die nicht so einfach zu ermittelnde relative Veränderung stimmt aber im Berührpunkt mit dem Wert überein.
Es lässt sich also festhalten:
- Nicht-lineare Funktionen: Soll die relative Veränderung einer nicht-linearen Funktion in einem bestimmten Punkt ermittelt werden, so wird sie (wenn möglich) dort linear genähert. Die Steigung der linearen Näherungsfunktion ist die an dieser Stelle vorliegende Steigung der betrachteten nicht-linearen Funktion, und es gilt dieselbe Anschauung wie bei Ableitungen linearer Funktionen. Dabei ist nur zu beachten, dass sich die relative Veränderung einer nicht-linearen Funktion von Punkt zu Punkt ändert.
- Während im Beispiel oben (Fahrzeugbewegung) für die durchschnittliche Geschwindigkeit die Zeitspanne angemessen willkürlich gewählt werden kann, ist die momentane Geschwindigkeit, wenn sie veränderlich ist, nur für kleine angebbar. Wie klein gewählt werden muss, hängt ab von der Anforderung an die Qualität der Näherung. In mathematischer Perfektion wird sie infinitesimal. Bei dieser wird für die relative Veränderung (wie schon oben angegeben) anstelle des Differenzenquotienten der Differenzialquotient geschrieben (in vereinfachter Schreibweise oder ).
Die Gewinnung der linearen Näherung einer nicht-linearen Funktion an einer bestimmten Stelle ist zentrale Aufgabe des Kalküls der Differentialrechnung. Bei einer mathematisch angebbaren Funktion (im Beispiel war das ) sollte sich die Ableitung ausrechnen lassen. Im Idealfall ist diese Berechnung sogar so allgemein, dass sie auf alle Punkte des Definitionsbereichs angewendet werden kann. Im Falle von kann gezeigt werden, dass an jeder Stelle die beste lineare Näherung die Steigung besitzen muss. Mit der Zusatzinformation, dass die lineare Funktion mit der Kurve im Punkt übereinstimmen muss, kann dann die vollständige Funktionsgleichung der linearen Näherungsfunktion aufgestellt werden.
Der Ansatz zur Bestimmung des Differentialquotienten liegt in der Berechnung des Grenzwerts (wie oben bei der momentanen Geschwindigkeit):
- oder in anderer Schreibweise
Bei einigen elementaren Funktionen wie Potenzfunktion, Exponentialfunktion, Logarithmusfunktion oder Sinusfunktion ist jeweils der Grenzwertprozess durchgeführt worden. Dabei ergibt sich jeweils eine Ableitungsfunktion. Darauf aufbauend sind Ableitungsregeln für die elementaren und auch für weitere Funktionen wie Summen, Produkte oder Verkettungen elementarer Funktionen aufgestellt worden.
Damit werden die Grenzübergänge nicht in jeder Anwendung neu vollzogen, sondern für die Rechenpraxis werden Ableitungsregeln angewendet. Die „Kunst“ der Differentialrechnung besteht „nur“ darin, kompliziertere Funktionen zu strukturieren und auf die Strukturelemente die jeweils zutreffende Ableitungsregel anzuwenden. Ein Beispiel folgt weiter hinten.
Berechnung von Grenzwerten
Jeder Differenzialquotient an einer vorgesehenen Stelle erscheint als unbestimmter Ausdruck vom Typ „“. Zu seiner Berechnung wird vom Differenzenquotient ausgegangen, und dessen Verhalten in der Umgebung der vorgesehenen Stelle wird untersucht, ob er die Tendenz hat, einen bestimmten Wert anzunehmen. Einige Grenzwerte, die für Ableitungsregeln benötigt werden, werden nachfolgend hergeleitet. Selbstverständlich dürfen dazu keine Regeln der Differenzialrechnung verwendet werden, da diese erst nach der Kenntnis der Grenzwerte aufgestellt werden können.
- Ein einfacher Fall 1
Ausgangspunkt ist der Differenzenquotient für die vorgesehene Funktion.
Wird die binomische Formel eingesetzt, so kürzt sich ein Summand heraus.
Für ist dieser Bruch unbestimmt. Aber für (dann und nur dann!) können Zähler und Nenner durch dividiert werden.
Für jedes ist dieser Ausdruck bestimmt, auch wenn man dem Wert nahe kommt. Er strebt im Grenzübergang nach
Im Weiteren werden hier nur Grenzwerte berechnet, und ihre Einsetzung in Differenzenquotienten erfolgt weiter hinten im Abschnitt Ableitungsberechnung.

- Fall 2
Für ist dieser Bruch unbestimmt. Zur Berechnung bei wird die Fläche eines Kreissektors mit dem Bogen verglichen mit den Flächen eines innen liegenden und eines außen liegenden Dreiecks gemäß der Zeichnung. Im gezeigten Quadranten gilt offensichtlich[3]
Bei kann diese Ungleichung mit multipliziert werden.
Für streben sowohl der linke als auch der rechte Ausdruck gegen eins. Damit muss auch der dazwischen liegende Ausdruck gegen eins streben. Für seinen Kehrwert gilt das ebenfalls. Für strebt er im Grenzübergang nach
- Zwischenüberlegung
Der Logarithmus dieses Ausdrucks, das ist , strebt für gegen „“. Dieser Logarithmus ist dort unbestimmt und damit auch der Ausdruck selber. Es ist aber bewiesen, dass
einen bestimmten endlichen Wert annimmt, der als Eulersche Zahl bezeichnet wird. Dieses wird unter dem verlinkten Stichwort behandelt und hier als bekannt vorausgesetzt.
- Fall 3
Für ist dieser Bruch unbestimmt. Aber für und ist die Substitution[4]
- ,
zulässig. Aufgelöst nach unter Verwendung des natürlichen Logarithmus ergibt das
Für streben und der Nenner gegen . Für jedes ist dieser Ausdruck bestimmt, auch wenn man dem Wert nahe kommt. Er strebt im Grenzübergang nach
Als Voraussetzung für diese Herleitung muss positiv sein. Für ist dieses erfüllt mit negativem . Nähert man sich bei dem Wert von der Seite her, so gilt derselbe Grenzübergang.
- Fall 4
Für ist dieser Bruch unbestimmt. Aber für ist die Substitution zulässig.[5]
Für strebt . Für jedes ist dieser Ausdruck bestimmt, auch wenn man dem Wert nahe kommt. Er strebt im Grenzübergang nach
Einordnung der Anwendungsmöglichkeiten
Extremwertprobleme
Eine wichtige Anwendung der Differentialrechnung besteht darin, dass mit Hilfe der Ableitung lokale Extremwerte einer Kurve bestimmt werden können. Anstatt also anhand einer Wertetabelle mechanisch nach Hoch- oder Tiefpunkten suchen zu müssen, liefert der Kalkül in einigen Fällen eine direkte Antwort. Liegt ein Hoch- oder Tiefpunkt vor, so besitzt die Kurve an dieser Stelle keinen „echten“ Anstieg, weshalb die optimale Linearisierung eine Steigung von 0 besitzt. Für die genaue Klassifizierung eines Extremwertes sind jedoch weitere lokale Daten der Kurve notwendig, denn eine Steigung von 0 ist nicht hinreichend für die Existenz eines Extremwertes (geschweige denn eines Hoch- oder Tiefpunktes).
In der Praxis treten Extremwertprobleme typischerweise dann auf, wenn Prozesse, zum Beispiel in der Wirtschaft, optimiert werden sollen. Oft liegen an den Randwerten jeweils ungünstige Ergebnisse, in Richtung „Mitte“ kommt es aber zu einer stetigen Steigerung, die dann irgendwo maximal werden muss. Zum Beispiel die optimale Wahl eines Verkaufspreises: Bei einem zu geringen Preis ist die Nachfrage nach einem Produkt zwar sehr groß, aber die Produktion kann nicht finanziert werden. Ist er andererseits zu hoch, so wird es im Extremfall gar nicht mehr gekauft. Daher liegt ein Optimum irgendwo „in der Mitte“. Voraussetzung dabei ist, dass der Zusammenhang in Form einer (stetig) differenzierbaren Funktion wiedergegeben werden kann.
Die Untersuchung einer Funktion auf Extremstellen ist Teil einer Kurvendiskussion. Die mathematischen Hintergründe sind im Abschnitt Anwendung höherer Ableitungen bereitgestellt.
Mathematische Modellierung
In der mathematischen Modellierung sollen komplexe Probleme in mathematischer Sprache erfasst und analysiert werden. Je nach Fragestellung sind das Untersuchen von Korrelationen oder Kausalitäten oder auch das Geben von Prognosen im Rahmen dieses Modells zielführend.
Besonders im Umfeld sog. Differentialgleichungen ist die Differentialrechnung zentrales Werkzeug bei der Modellierung. Diese Gleichungen treten zum Beispiel auf, wenn es eine kausale Beziehung zwischen dem Bestand einer Größe und deren zeitlicher Veränderung gibt. Ein alltägliches Beispiel könnte sein:
- Je mehr Einwohner eine Stadt besitzt, desto mehr Leute wollen dort hinziehen.
Etwas konkreter könnte dies zum Beispiel heißen, dass bei jetzigen Einwohnern durchschnittlich Personen in den kommenden 10 Jahren zuziehen werden, bei Einwohnern durchschnittlich Personen in den kommenden 10 Jahren usw. – um nicht alle Zahlen einzeln ausführen zu müssen: Leben Personen in der Stadt, so wollen so viele Menschen hinzuziehen, dass nach 10 Jahren weitere hinzukommen würden. Besteht eine derartige Kausalität zwischen Bestand und zeitlicher Veränderung, so kann gefragt werden, ob aus diesen Daten eine Prognose für die Einwohnerzahl nach 10 Jahren abgeleitet werden kann, wenn die Stadt im Jahr 2020 zum Beispiel Einwohner hatte. Es wäre dabei falsch zu glauben, dass dies sein werden, da sich mit steigender Einwohnerzahl auch die Nachfrage nach Wohnraum wiederum zunehmend steigern wird. Der Knackpunkt zum Verständnis des Zusammenhangs ist demnach erneut dessen Lokalität: Besitzt die Stadt Einwohner, so wollen zu diesem Zeitpunkt Menschen pro 10 Jahre hinzuziehen. Aber einen kurzen Augenblick später, wenn weitere Menschen hinzugezogen sind, sieht die Lage wieder anders aus. Wird dieses Phänomen zeitlich beliebig engmaschig gedacht, ergibt sich ein „differentieller“ Zusammenhang. Allerdings eignet sich die kontinuierliche Herangehensweise in vielen Fällen auch bei diskreten Problemstellungen.[6]
Mit Hilfe der Differentialrechnung kann aus so einem kausalen Zusammenhang zwischen Bestand und Veränderung in vielen Fällen ein Modell hergeleitet werden, was den komplexen Zusammenhang auflöst, und zwar in dem Sinne, dass zum Schluss eine Bestandsfunktion explizit angegeben werden kann. Setzt man in diese Funktion dann zum Beispiel den Wert 10 Jahre ein, so ergibt sich eine Prognose für die Stadtbewohneranzahl im Jahr 2030. Im Falle oberen Modells wird eine Bestandsfunktion gesucht mit , in 10 Jahren, und . Die Lösung ist dann
mit der natürlichen Exponentialfunktion (natürlich bedeutet, dass der Proportionalitätsfaktor zwischen Bestand und Veränderung einfach gleich 1 ist) und für das Jahr 2030 lautet die geschätzte Prognose Mio. Einwohner. Die Proportionalität zwischen Bestand und Veränderungsrate führt also zu exponentiellem Wachstum und ist klassisches Beispiel eines selbstverstärkenden Effektes. Analoge Modelle funktionieren beim Populationswachstum (Je mehr Individuen, desto mehr Geburten) oder der Verbreitung einer ansteckenden Krankheit (Je mehr Erkrankte, desto mehr Ansteckungen). In vielen Fällen stoßen diese Modelle jedoch an eine Grenze, wenn sich der Prozess aufgrund natürlicher Beschränkungen (wie eine Obergrenze der Gesamtbevölkerung) nicht beliebig fortsetzen lässt. In diesen Fällen sind ähnliche Modelle, wie das logistische Wachstum, geeigneter.[7]
Numerische Verfahren
Die Eigenschaft einer Funktion, differenzierbar zu sein, ist bei vielen Anwendungen von Vorteil, da dies der Funktion mehr Struktur verleiht. Ein Beispiel ist das Lösen von Gleichungen. Bei einigen mathematischen Anwendungen ist es notwendig, den Wert einer (oder mehrerer) Unbekannten zu finden, die Nullstelle einer Funktion ist. Es ist dann . Je nach Beschaffenheit von können Strategien entwickelt werden, eine Nullstelle zumindest näherungsweise anzugeben, was in der Praxis meist vollkommen ausreicht. Ist in jedem Punkt differenzierbar mit Ableitung , so kann in vielen Fällen das Newton-Verfahren helfen. Bei diesem spielt die Differentialrechnung insofern eine direkte Rolle, als beim schrittweisen Vorgehen immer wieder eine Ableitung explizit berechnet werden muss.[8]
Ein weiterer Vorteil der Differentialrechnung ist, dass in vielen Fällen komplizierte Funktionen, wie Wurzeln oder auch Sinus und Kosinus, anhand einfacher Rechenregeln wie Addition und Multiplikation gut angenähert werden können. Ist die Funktion an einem benachbarten Wert leicht auszuwerten, ist dies von großem Nutzen. Wird zum Beispiel nach einem Näherungswert für die Zahl gesucht, so liefert die Differentialrechnung für die Linearisierung
denn es gilt nachweislich . Sowohl Funktion als auch erste Ableitung konnten an der Stelle gut berechnet werden, weil es sich dabei um eine Quadratzahl handelt. Einsetzen von ergibt , was mit dem exakten Ergebnis bis auf einen Fehler kleiner als übereinstimmt.[9] Unter Einbezug höherer Ableitungen kann die Genauigkeit solcher Approximationen zusätzlich gesteigert werden, da dann nicht nur linear, sondern quadratisch, kubisch usw. angenähert wird, siehe auch Taylor-Reihe.
Reine Mathematik

Auch in der reinen Mathematik spielt die Differentialrechnung als ein Kern der Analysis eine bedeutende Rolle. Ein Beispiel ist die Differentialgeometrie, die sich mit Figuren beschäftigt, die eine differenzierbare Oberfläche (ohne Knicke usw.) haben. Zum Beispiel kann auf eine Kugeloberfläche in jedem Punkt tangential eine Ebene platziert werden. Anschaulich: Steht man an einem Erdpunkt, so hat man das Gefühl, die Erde sei flach, wenn man seinen Blick in der Tangentialebene schweifen lässt. In Wahrheit ist die Erde jedoch nur lokal flach: Die angelegte Ebene dient der (durch Linearisierung) vereinfachten Darstellung der komplizierteren Krümmung. Global hat sie als Kugeloberfläche eine völlig andere Gestalt.
Die Methoden der Differentialgeometrie sind äußerst bedeutend für die theoretische Physik. So können Phänomene wie Krümmung oder Raumzeit über Methoden der Differentialrechnung beschrieben werden. Auch die Frage, was der kürzeste Abstand zwischen zwei Punkten auf einer gekrümmten Fläche (zum Beispiel der Erdoberfläche) ist, kann mit diesen Techniken formuliert und oft auch beantwortet werden.
Auch bei der Erforschung von Zahlen als solchen, also im Rahmen der Zahlentheorie, hat sich die Differentialrechnung in der analytischen Zahlentheorie bewährt. Die grundlegende Idee der analytischen Zahlentheorie ist die Umwandlung von bestimmten Zahlen, über die man etwas lernen möchte, in Funktionen. Haben diese Funktionen „gute Eigenschaften“ wie etwa Differenzierbarkeit, so hofft man, über die damit einhergehenden Strukturen Rückschlüsse auf die ursprünglichen Zahlen ziehen zu können. Es hat sich dabei häufig bewährt, zur Perfektionierung der Analysis von den reellen zu den komplexen Zahlen überzugehen (siehe auch komplexe Analysis), also die Funktionen über einem größeren Zahlenbereich zu studieren. Ein Beispiel ist die Analyse der Fibonacci-Zahlen , deren Bildungsgesetz vorschreibt, dass eine neue Zahl stets aus der Summe der beiden vorangehenden entstehen soll. Ansatz der analytischen Zahlentheorie ist die Bildung der erzeugenden Funktion
also eines „unendlich langen“ Polynoms (einer sog. Potenzreihe), dessen Koeffizienten genau die Fibonacci-Zahlen sind. Für hinreichend kleine Zahlen ist dieser Ausdruck sinnvoll, weil die Potenzen dann viel schneller gegen 0 gehen als die Fibonacci-Zahlen gegen Unendlich, womit sich langfristig alles bei einem endlichen Wert einpendelt. Es ist für diese Werte möglich, die Funktion explizit zu berechnen durch
Das Nennerpolynom „spiegelt“ dabei genau das Verhalten der Fibonacci-Zahlen „wider“ – es ergibt sich in der Tat durch termweises Verrechnen. Mit Hilfe der Differentialrechnung lässt sich andererseits zeigen, dass die Funktion ausreicht, um die Fibonacci-Zahlen (ihre Koeffizienten) eindeutig zu charakterisieren. Da es sich aber um eine schlichte rationale Funktion handelt, lässt sich dadurch die für jede Fibonacci-Zahl gültige exakte Formel
mit dem goldenen Schnitt herleiten, wenn und gesetzt wird. Die exakte Formel vermag eine Fibonacci-Zahl zu berechnen, ohne die vorherigen zu kennen. Der Schluss wird über einen sog. Koeffizientenvergleich gezogen und nutzt aus, dass das Polynom als Nullstellen und besitzt.[10]
Der höherdimensionale Fall
Die Differentialrechnung kann auf den Fall „höherdimensionaler Funktionen“ verallgemeinert werden. Damit ist gemeint, dass sowohl Eingabe- als auch Ausgabewerte der Funktion nicht bloß Teil des eindimensionalen reellen Zahlenstrahls, sondern auch Punkte eines höherdimensionalen Raums sind. Ein Beispiel ist die Vorschrift
zwischen jeweils zweidimensionalen Räumen. Das Funktionsverständnis als Tabelle bleibt hier identisch, nur dass diese mit „vier Spalten“ „deutlich mehr“ Einträge besitzt. Auch mehrdimensionale Abbildungen können in manchen Fällen an einem Punkt linearisiert werden. Allerdings ist dabei nun angemessen zu beachten, dass es sowohl mehrere Eingabedimensionen als auch mehrere Ausgabedimensionen geben kann: Der korrekte Verallgemeinerungsweg liegt darin, dass die Linearisierung in jeder Komponente der Ausgabe jede Variable auf lineare Weise berücksichtigt. Das zieht für obere Beispielfunktion eine Approximation der Form
nach sich. Diese ahmt dann die gesamte Funktion in der Nähe der Eingabe sehr gut nach.[11] In jeder Komponente wird demnach für jede Variable eine „Steigung“ angegeben – diese wird dann das lokale Verhalten der Komponentenfunktion bei kleiner Änderung in dieser Variablen messen. Diese Steigung wird auch als partielle Ableitung bezeichnet.[12] Die korrekten konstanten Abschnitte berechnen sich exemplarisch durch bzw. . Wie auch im eindimensionalen Fall hängen die Steigungen (hier ) stark von der Wahl des Punktes (hier ) ab, an dem abgeleitet wird. Die Ableitung ist demnach keine Zahl mehr, sondern ein Verband aus mehreren Zahlen – in diesem Beispiel sind es vier – und diese Zahlen sind im Regelfall bei allen Eingaben unterschiedlich. Es wird allgemein für die Ableitung auch
geschrieben, womit alle „Steigungen“ in einer sog. Matrix versammelt sind. Man bezeichnet diesen Term auch als Jacobi-Matrix oder Funktionalmatrix.[13]
Beispiel: Wird oben gesetzt, so kann man zeigen, dass folgende lineare Approximation bei sehr kleinen Änderungen von und sehr gut ist:
Zum Beispiel gilt
und
Hat man im ganz allgemeinen Fall Variablen und Ausgabekomponenten, so gibt es kombinatorisch gesehen insgesamt „Steigungen“, also partielle Ableitungen. Im klassischen Fall gibt es wegen eine Steigung und im oberen Beispiel sind es „Steigungen“.[14]
Geschichte


Die Aufgabenstellung der Differentialrechnung bildete sich als Tangentenproblem ab dem 17. Jahrhundert heraus. Hierunter versteht man die Aufgabe, bei einer beliebigen Kurve in einem beliebigen Punkt die Tangente zu bestimmen.[15] Ein naheliegender Lösungsansatz bestand darin, die Tangente an eine Kurve durch ihre Sekante über einem endlichen (endlich heißt hier: größer als null), aber beliebig kleinen Intervall zu approximieren. Dabei war die technische Schwierigkeit zu überwinden, mit einer solchen infinitesimal kleinen Intervallbreite zu rechnen. Die ersten Anfänge der Differentialrechnung gehen auf Pierre de Fermat zurück. Er entwickelte um 1628 eine Methode, Extremstellen algebraischer Terme zu bestimmen und Tangenten an Kegelschnitte und andere Kurven zu berechnen. Seine „Methode“ war rein algebraisch. Fermat betrachtete keine Grenzübergänge und schon gar keine Ableitungen. Gleichwohl lässt sich seine „Methode“ mit modernen Mitteln der Analysis interpretieren und rechtfertigen, und sie hat Mathematiker wie Newton und Leibniz nachweislich inspiriert. Einige Jahre später wählte René Descartes einen anderen algebraischen Zugang, indem er an eine Kurve einen Kreis anlegte. Dieser schneidet die Kurve in zwei nahe beieinanderliegenden Punkten; es sei denn, er berührt die Kurve. Dieser Ansatz ermöglichte es ihm, für spezielle Kurven die Steigung der Tangente zu bestimmen.[16]
Ende des 17. Jahrhunderts gelang es Isaac Newton und Gottfried Wilhelm Leibniz mit unterschiedlichen Ansätzen unabhängig voneinander, widerspruchsfrei funktionierende Kalküle zu entwickeln. Während Newton das Problem physikalisch über das Momentangeschwindigkeitsproblem anging,[17] löste es Leibniz geometrisch über das Tangentenproblem. Ihre Arbeiten erlaubten das Abstrahieren von rein geometrischer Vorstellung und werden deshalb als Beginn der Analysis betrachtet. Bekannt wurden sie vor allem durch das Buch Analyse des Infiniment Petits pour l’Intelligence des Lignes Courbes[18] des Adligen Guillaume François Antoine, Marquis de L’Hospital, der bei Johann I Bernoulli Privatunterricht nahm und dessen Forschung zur Analysis so publizierte. Darin heißt es:
„Die Reichweite dieses Kalküls ist unermesslich: Er lässt sich sowohl auf mechanische als auch geometrische Kurven anwenden; Wurzelzeichen bereiten ihm keine Schwierigkeiten und sind oftmals sogar angenehm im Umgang; er lässt sich auf so viele Variablen erweitern, wie man sich nur wünschen kann; der Vergleich unendlich kleiner Größen aller Art gelingt mühelos. Und er erlaubt eine unendliche Zahl an überraschenden Entdeckungen über gekrümmte wie geradlinige Tangenten, Fragen De maximis & minimis, Wendepunkte und Spitzen von Kurven, Evoluten, Spiegelungs- und Brechungskaustiken, &c. wie wir in diesem Buch sehen werden.“[19]
Die heute bekannten Ableitungsregeln basieren vor allem auf den Werken von Leonhard Euler, der den Funktionsbegriff prägte.
Newton und Leibniz arbeiteten mit beliebig kleinen positiven Zahlen.[20] Dies wurde bereits von Zeitgenossen als unlogisch kritisiert, beispielsweise von George Berkeley in der polemischen Schrift The analyst; or, a discourse addressed to an infidel mathematician.[21] Erst in den 1960ern konnte Abraham Robinson diese Verwendung infinitesimaler Größen mit der Entwicklung der Nichtstandardanalysis auf ein mathematisch-axiomatisch sicheres Fundament stellen. Trotz der herrschenden Unsicherheit wurde die Differentialrechnung aber konsequent weiterentwickelt, in erster Linie wegen ihrer zahlreichen Anwendungen in der Physik und in anderen Gebieten der Mathematik. Symptomatisch für die damalige Zeit war das von der Preußischen Akademie der Wissenschaften 1784 veröffentlichte Preisausschreiben:
„… Die höhere Geometrie benutzt häufig unendlich große und unendlich kleine Größen; jedoch haben die alten Gelehrten das Unendliche sorgfältig vermieden, und einige berühmte Analysten unserer Zeit bekennen, dass die Wörter unendliche Größe widerspruchsvoll sind. Die Akademie verlangt also, dass man erkläre, wie aus einer widersprechenden Annahme so viele richtige Sätze entstanden sind, und dass man einen sicheren und klaren Grundbegriff angebe, welcher das Unendliche ersetzen dürfte, ohne die Rechnung zu schwierig oder zu lang zu machen …“[22]
Erst zum Anfang des 19. Jahrhunderts gelang es Augustin-Louis Cauchy, der Differentialrechnung die heute übliche logische Strenge zu geben, indem er von den infinitesimalen Größen abging und die Ableitung als Grenzwert von Sekantensteigungen (Differenzenquotienten) definierte.[23] Die heute benutzte Definition des Grenzwerts wurde schließlich von Karl Weierstraß im Jahr 1861 formuliert.[24]
Definition
Sekanten- und Tangentensteigung
Ausgangspunkt für die Definition der Ableitung ist die Näherung der Tangentensteigung durch eine Sekantensteigung (manchmal auch Sehnensteigung genannt). Gesucht sei die Steigung einer Funktion in einem Punkt . Man berechnet zunächst die Steigung der Sekante an über einem endlichen Intervall der Länge :
- Sekantensteigung = .
Die Sekantensteigung ist also der Quotient zweier Differenzen; sie wird deshalb auch Differenzenquotient genannt. Mit der Kurznotation für kann man die Sekantensteigung abgekürzt als schreiben. Der Ausdruck verdeutlicht also die beliebig klein werdende Differenz zwischen der Stelle, an der abgeleitet werden soll, und einem benachbarten Punkt. In der Literatur wird jedoch, wie auch im Folgenden, in vielen Fällen aus Gründen der Einfachheit das Symbol statt verwendet.
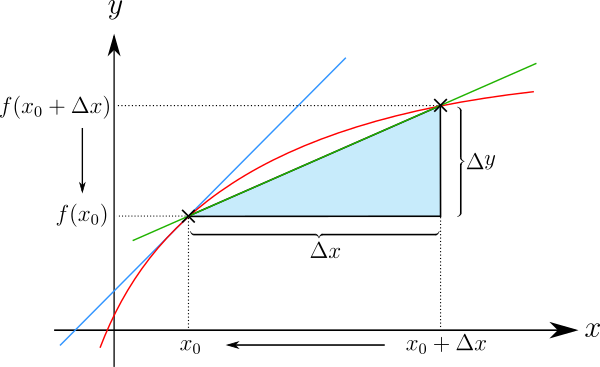
Um eine Tangentensteigung zu berechnen, muss man die beiden Punkte, durch die die Sekante gezogen wird, immer weiter aneinander rücken. Dabei gehen sowohl als auch gegen Null. Der Quotient bleibt aber in vielen Fällen endlich. Auf diesem Grenzübergang beruht die folgende Definition.
Differenzierbarkeit


Eine Funktion , die ein offenes Intervall in die reellen Zahlen abbildet, heißt differenzierbar an der Stelle , falls der Grenzwert
- (mit )
existiert. Dieser Grenzwert heißt Differentialquotient oder Ableitung von nach an der Stelle und wird als
- oder oder oder
notiert.[25][26] Gesprochen werden diese Notationen als „f Strich von x null“, „d f von x nach d x an der Stelle x gleich x null“, „d f nach d x von x null“ respektive „d nach d x von f von x null“. Im später folgenden Abschnitt Notationen werden noch weitere Varianten angeführt, um die Ableitung einer Funktion zu notieren.
Im Laufe der Zeit wurde folgende gleichwertige Definition gefunden, die sich im allgemeineren Kontext komplexer oder mehrdimensionaler Funktionen als leistungsfähiger erwiesen hat: Eine Funktion heißt an einer Stelle differenzierbar, falls eine Konstante existiert, sodass
Der Zuwachs der Funktion , wenn man sich von nur wenig entfernt, etwa um den Wert , lässt sich also durch sehr gut approximieren. Man nennt deshalb die lineare Funktion , für die also für alle gilt, auch die Linearisierung von an der Stelle .[27]
Eine weitere Definition ist: Es gibt eine an der Stelle stetige Funktion mit und eine Konstante , sodass für alle gilt
- .
Die Bedingungen und dass an der Stelle stetig ist, bedeuten gerade, dass das „Restglied“ für gegen gegen konvergiert.[27]
In beiden Fällen ist die Konstante eindeutig bestimmt und es gilt . Der Vorteil dieser Formulierung ist, dass Beweise einfacher zu führen sind, da kein Quotient betrachtet werden muss. Diese Darstellung der besten linearen Approximation wurde schon von Karl Weierstraß, Henri Cartan und Jean Dieudonné konsequent angewandt und wird auch Weierstraßsche Zerlegungsformel genannt.
Bezeichnet man eine Funktion als differenzierbar, ohne sich auf eine bestimmte Stelle zu beziehen, dann bedeutet dies die Differenzierbarkeit an jeder Stelle des Definitionsbereiches, also die Existenz einer eindeutigen Tangente für jeden Punkt des Graphen.
Jede differenzierbare Funktion ist stetig, die Umkehrung gilt jedoch nicht.[27] Noch Anfang des 19. Jahrhunderts war man überzeugt, dass eine stetige Funktion höchstens an wenigen Stellen nicht differenzierbar sein könne (wie die Betragsfunktion). Bernard Bolzano konstruierte dann als erster Mathematiker tatsächlich eine Funktion, die später Bolzanofunktion genannt wurde, die überall stetig, aber nirgends differenzierbar ist, was in der Fachwelt allerdings nicht bekannt wurde. Karl Weierstraß fand dann in den 1860er Jahren ebenfalls eine derartige Funktion (siehe Weierstraß-Funktion), was diesmal unter Mathematikern Wellen schlug. Ein bekanntes mehrdimensionales Beispiel für eine stetige, nicht differenzierbare Funktion ist die von Helge von Koch 1904 vorgestellte Koch-Kurve.[28]
Ableitungsfunktion

Die Ableitung der Funktion an der Stelle , bezeichnet mit , beschreibt lokal das Verhalten der Funktion in der Umgebung der betrachteten Stelle . In einigen Fällen ist es möglich, an jedem Punkt des Funktionsgraphen eine Linearisierung vorzunehmen. Dies erlaubt die Definition einer Ableitungsfunktion (oder kurz Ableitung) , die jedem Element des Definitionsbereichs der Ausgangsfunktion die Steigung der dortigen Linearisierung zuordnet. Man sagt in diesem Falle, „ ist in differenzierbar“.[29]
Beispielsweise hat die Quadratfunktion mit an einer beliebigen Stelle die Ableitung die Quadratfunktion ist also auf der Menge der reellen Zahlen differenzierbar. Die zugehörige Ableitungsfunktion ist gegeben durch mit .
Die Ableitungsfunktion ist im Normalfall eine andere Funktion als die ursprünglich betrachtete. Einzige Ausnahme sind die Vielfachen der natürlichen Exponentialfunktion mit beliebigem – unter denen, wie die Wahl zeigt, auch alle Funktionen mit beliebigem enthalten sind (deren Graph aus dem der Exponentialfunktion durch „seitliche“ Verschiebung um entsteht und zu diesem daher kongruent ist).
Ist die Ableitung stetig, dann heißt stetig differenzierbar. In Anlehnung an die Bezeichnung für die Gesamtheit (den Raum) der stetigen Funktionen mit Definitionsmenge wird der Raum der auf stetig differenzierbaren Funktionen mit abgekürzt.[30]
Notationen
Geschichtlich bedingt gibt es unterschiedliche Notationen, um die Ableitung einer Funktion darzustellen.
Lagrange-Notation
In diesem Artikel wurde bisher hauptsächlich die Notation für die Ableitung von verwendet. Diese Notation geht auf den Mathematiker Joseph-Louis Lagrange zurück, der sie 1797 einführte.[31] Bei dieser Notation wird die zweite Ableitung von mit und die -te Ableitung mittels bezeichnet.
Newton-Notation
Isaac Newton – neben Leibniz der Begründer der Differentialrechnung – notierte die erste Ableitung von mit , entsprechend notierte er die zweite Ableitung durch .[32] Heutzutage wird diese Schreibweise häufig in der Physik, insbesondere in der Mechanik, für die Ableitung nach der Zeit verwendet.[33]
Leibniz-Notation
Gottfried Wilhelm Leibniz führte für die erste Ableitung von (nach der Variablen ) die Notation ein.[34] Gelesen wird dieser Ausdruck als „d f von x nach d x“. Für die zweite Ableitung notierte Leibniz und die -te Ableitung wird mittels bezeichnet.[35] Bei der Schreibweise von Leibniz handelt es sich nicht um einen Bruch. Die Symbole und werden „Differentiale“ genannt, haben aber in der modernen Differentialrechnung (abgesehen von der Theorie der Differentialformen) lediglich eine symbolische Bedeutung und sind nur in dieser Schreibweise als formaler Differentialquotient erlaubt. In manchen Anwendungen (Kettenregel, Integration mancher Differentialgleichungen, Integration durch Substitution) rechnet man mit ihnen aber so, als wären sie gewöhnliche Terme.
Euler-Notation
Die Notation oder für die erste Ableitung von geht auf Leonhard Euler zurück. Dabei wird die Ableitung als Operator – also als eine besondere Funktion, die selbst auf Funktionen arbeitet, aufgefasst. Diese Idee geht auf den Mathematiker Louis François Antoine Arbogast zurück. Die zweite Ableitung wird in dieser Notation mittels oder und die -te Ableitung durch oder dargestellt.[36]
Ableitungsberechnung
Das Berechnen der Ableitung einer Funktion wird Differentiation oder Differenziation genannt; sprich, man differenziert diese Funktion.
Um die Ableitung elementarer Funktionen (z. B. , , …) zu berechnen, hält man sich eng an die oben angegebene Definition, berechnet explizit einen Differenzenquotienten und lässt dann gegen Null gehen. Dieses Verfahren ist jedoch meistens umständlich. Bei der Lehre der Differentialrechnung wird diese Art der Rechnung daher nur wenige Male vollzogen. Später greift man auf bereits bekannte Ableitungsfunktionen zurück oder schlägt Ableitungen nicht ganz so geläufiger Funktionen in einem Tabellenwerk nach (z. B. im Bronstein-Semendjajew, siehe auch Tabelle von Ableitungs- und Stammfunktionen) und berechnet die Ableitung zusammengesetzter Funktionen mit Hilfe der Ableitungsregeln.
Ableitungen elementarer Funktionen
Für die Berechnung der Ableitungsfunktion einer elementaren Funktion an einer vorgesehenen Stelle wird der zugehörige Differenzenquotient gebildet, der in der Umgebung mit gültig ist, und dann wird der Grenzübergang vollzogen.
Natürliche Potenzen
Der Fall ist bereits weiter oben behandelt worden. Der zugehörige Differenzenquotient ergibt sich zu
Wenn ist, lässt sich kürzen,
und die Annäherung führt auf
Allgemein für eine natürliche Zahl mit wird der binomische Lehrsatz herangezogen:
Wenn für alle endlichen Werte von endlich ist, ist auch endlich. Der in der letzten Gleichung vor stehende Faktor führt auf . Damit entsteht
Zwei Ergänzungen:
- Ein konstanter Summand in kürzt sich in heraus, noch bevor der Grenzübergang vollzogen wird.
- Ein konstanter Faktor in kann in ausgeklammert und vor den Bruch gezogen werden.
Exponentialfunktion

Mit der Exponentialfunktion ergibt sich der Differenzenquotient
Für jedes gilt
Damit kann im Zähler ausgeklammert werden.
Mit dem oben hergeleiteten Grenzübergang
entsteht
Darin ist der natürliche Logarithmus von . Speziell für die Eulersche Zahl ist . Damit entsteht die auszeichnende Zusatzeigenschaft
Logarithmus
Mit der Logarithmusfunktion zur Basis ergibt sich der Differenzenquotient

Für jedes gilt
Mit dem oben hergeleiteten Grenzübergang
und mit der Basisumrechnung entsteht
Dieses existiert nur für . Für existiert die Funktion .[37] Mit der Substitution und der Kettenregel ergibt ihre Ableitung
Beide Ableitungen können zusammengefasst werden für zu
Speziell für den natürlichen Logarithmus gilt
Sinus und Kosinus
Mit der Sinusfunktion ergibt sich der Differenzenquotient
Mit dem Additionstheorem
gilt
Mit dem oben hergeleiteten Grenzübergang
und mit entsteht
Für die Kosinusfunktion führt eine entsprechende Rechnung mit
auf
Weitere elementare Funktionen
Mit den vorstehenden Ableitungen können Ableitungsfunktionen für weitere Funktionen aufgestellt werden. Dazu werden zusätzlich die Ableitungsregeln für die Grundrechenarten, die Kettenregel und die Umkehrregel benötigt.
Allgemeine Potenzen
Die Funktion ist bisher nur für als natürliche Zahl abgeleitet worden. Die Anwendbarkeit der zugehörigen Ableitungsregel lässt sich bei auf reelle Exponenten erweitern. Mit der Substitution[38]
ist
Wird dieses mit der Kettenregel differenziert, so entsteht das bekannte Ergebnis:
Eine Anwendung ist die Ableitung der Wurzelfunktion. Für gilt mit
Der Fall betrifft die Quadratwurzel:
Für gilt
Tangens und Kotangens
Mit Hilfe der Quotientenregel und den Ableitungsfunktionen für Sinus und Kosinus können auch die Ableitungsfunktionen für Tangens und Kotangens aufgestellt werden. Es gilt
Dabei wurde die als „Trigonometrischer Pythagoras“ bezeichnete Formel verwendet. Ebenso wird gewonnen
Arkussinus und Arkuskosinus
Arkussinus und Arkuskosinus sind als Umkehrfunktionen von Sinus und Kosinus definiert. Die Ableitungen werden mittels der Umkehrregel berechnet. Setzt man , so folgt im Bereich
Für den Arkuskosinus ergibt sich mit ebenso
Arkustangens und Arkuskotangens
Arkustangens und Arkuskotangens sind als Umkehrfunktionen von Tangens und Kotangens definiert. Setzt man , so folgt mittels der Umkehrregel
Für den Arkuskotangens ergibt sich mit ebenso
Zusammengesetzte Funktion
Zusammengesetzte Funktionen lassen sich so weit strukturieren, bis sich zu jedem Strukturelement die jeweils zutreffende elementare Ableitungsregel finden lässt. Dazu gibt es die Summenregel, die Produktregel, die Quotientenregel und die Kettenregel. Da diese in eigenen Artikeln erläutert werden, wird hier nur ein Beispiel vorgestellt.
mit ist ableitbar nach als Potenz mit ist ableitbar nach als Summe mit einer Konstanten mit ist ableitbar nach als trigonometrische Funktion ist ableitbar nach als Potenz mit konstantem Faktor
Nach der Kettenregel ergibt sich
Zusammenfassung
Hier werden die Ableitungsregeln elementarer und zusammengesetzter Funktionen zusammengefasst. Eine ausführliche Liste findet sich unter Tabelle von Ableitungs- und Stammfunktionen.
| Anmerkung | ||
|---|---|---|
| Elementares | ||
| konstanter Faktor bleibt erhalten | ||
| konstanter Summand verschwindet | ||
| Potenzfunktion | ||
| Exponentialfunktion | ||
| Logarithmusfunktion | ||
| Trigonometrische Funktionen | ||
| Hyperbelfunktionen | ||
| Summenregel | ||
| Produktregel | ||
| Quotientenregel | ||
oder | Kettenregel mit | |
oder | Umkehrregel mit oder nach aufgelöst |
Höhere Ableitungen
Ist die Ableitung einer Funktion wiederum differenzierbar, so lässt sich die zweite Ableitung von als Ableitung der ersten definieren. Auf dieselbe Weise können dann auch dritte, vierte etc. Ableitungen definiert werden. Eine Funktion kann dementsprechend einmal differenzierbar, zweimal differenzierbar etc. sein.
Ist die erste Ableitung eines Weges nach der Zeit eine Geschwindigkeit, so kann die zweite Ableitung als Beschleunigung und die dritte Ableitung als Ruck interpretiert werden.
Wenn Politiker sich über den „Rückgang des Anstiegs der Arbeitslosenzahl“ äußern, dann sprechen sie von der zweiten Ableitung (Änderung des Anstiegs), um die Aussage der ersten Ableitung (Anstieg der Arbeitslosenzahl) zu relativieren.
Höhere Ableitungen können auf verschiedene Weisen geschrieben werden:
oder im physikalischen Fall (bei einer Ableitung nach der Zeit)
Für die formale Bezeichnung beliebiger Ableitungen legt man außerdem und fest.
Höhere Differentialoperatoren
Ist eine natürliche Zahl und offen, so wird der Raum der in -mal stetig differenzierbaren Funktionen mit bezeichnet. Der Differentialoperator induziert damit eine Kette von linearen Abbildungen
und damit allgemein für :
Dabei bezeichnet den Raum der in stetigen Funktionen. Exemplarisch: Wird ein durch Anwenden von einmal abgeleitet, kann das Ergebnis im Allgemeinen nur noch -mal abgeleitet werden usw. Jeder Raum ist eine -Algebra, da nach der Summen- bzw. der Produktregel Summen und auch Produkte von -mal stetig differenzierbaren Funktionen wieder -mal stetig differenzierbar sind. Es gilt zudem die aufsteigende Kette von echten Inklusionen
denn offenbar ist jede mindestens -mal stetig differenzierbare Funktion auch -mal stetig differenzierbar usw., jedoch zeigen die Funktionen
exemplarisch Beispiele für Funktionen aus , wenn – was ohne Beschränkung der Allgemeinheit möglich ist – angenommen wird.[39]
Höhere Ableitungsregeln
Die Ableitung -ter Ordnung für ein Produkt aus zwei -mal differenzierbaren Funktionen und ergibt sich aus
- .
Die hier auftretenden Ausdrücke der Form sind Binomialkoeffizienten. Die Formel ist eine Verallgemeinerung der Produktregel.
Diese Formel ermöglicht die geschlossene Darstellung der -ten Ableitung der Komposition zweier -mal differenzierbarer Funktionen. Sie verallgemeinert die Kettenregel auf höhere Ableitungen.
Taylorformeln mit Restglied
Ist eine in einem Intervall -mal stetig differenzierbare Funktion, dann gilt für alle und aus die sogenannte Taylorformel:
mit dem -ten Taylorpolynom an der Entwicklungsstelle
und dem -ten Restglied
mit einem .[40] Eine beliebig oft differenzierbare Funktion wird glatte Funktion genannt. Da sie alle Ableitungen besitzt, kann die oben angegebene Taylorformel zur Taylorreihe von mit Entwicklungspunkt erweitert werden:
Es ist jedoch nicht jede glatte Funktion durch ihre Taylorreihe darstellbar, siehe unten.
Glatte Funktionen
Funktionen, die an jeder Stelle ihres Definitionsbereichs beliebig oft differenzierbar sind, bezeichnet man auch als glatte Funktionen. Die Menge aller in einer offenen Menge glatten Funktionen wird meist mit bezeichnet. Sie trägt die Struktur einer -Algebra (skalare Vielfache, Summen und Produkte glatter Funktionen sind wieder glatt) und ist gegeben durch
wobei alle in -mal stetig differenzierbaren Funktionen bezeichnet.[30] Häufig findet man in mathematischen Betrachtungen den Begriff hinreichend glatt. Damit ist gemeint, dass die Funktion mindestens so oft differenzierbar ist, wie es nötig ist, um den aktuellen Gedankengang durchzuführen.
Analytische Funktionen
Der obere Begriff der Glattheit kann weiter verschärft werden. Eine Funktion heißt reell analytisch, wenn sie sich in jedem Punkt lokal in eine Taylorreihe entwickeln lässt, also
für alle und alle hinreichend kleinen Werte von . Analytische Funktionen haben starke Eigenschaften und finden besondere Aufmerksamkeit in der komplexen Analysis. Dort werden dementsprechend keine reell, sondern komplex analytischen Funktionen studiert. Ihre Menge wird meist mit bezeichnet und es gilt . Insbesondere ist jede analytische Funktion glatt, aber nicht umgekehrt. Die Existenz aller Ableitungen ist also nicht hinreichend dafür, dass die Taylorreihe die Funktion darstellt, wie das folgende Gegenbeispiel
einer nicht analytischen glatten Funktion zeigt.[41] Alle reellen Ableitungen dieser Funktion verschwinden in 0, aber es handelt sich nicht um die Nullfunktion. Daher wird sie an der Stelle 0 nicht durch ihre Taylorreihe dargestellt.
Anwendungen
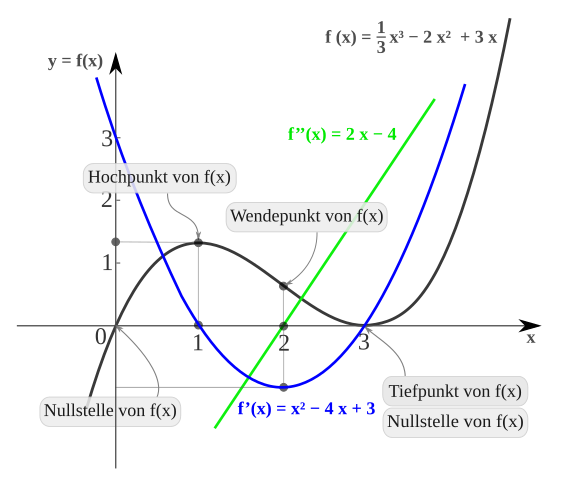
Eine wichtige Anwendung der Differentialrechnung in einer Variablen ist die Bestimmung von Extremwerten, meist zur Optimierung von Prozessen, wie etwa im Kontext von Kosten, Material oder Energieaufwand.[42] Die Differentialrechnung stellt eine Methode bereit, Extremstellen zu finden, ohne dabei unter Aufwand numerisch suchen zu müssen. Man macht sich zu Nutze, dass an einer lokalen Extremstelle notwendigerweise die erste Ableitung der Funktion gleich 0 sein muss. Es muss also gelten, wenn eine lokale Extremstelle ist. Allerdings bedeutet andersherum noch nicht, dass es sich bei um ein Maximum oder Minimum handelt. In diesem Fall werden mehr Informationen benötigt, um eine eindeutige Entscheidung treffen zu können, was meist durch Betrachten höherer Ableitungen bei möglich ist.
Eine Funktion kann einen Maximal- oder Minimalwert haben, ohne dass die Ableitung an dieser Stelle existiert, jedoch kann in diesem Falle die Differentialrechnung nicht verwendet werden. Im Folgenden werden daher nur zumindest lokal differenzierbare Funktionen betrachtet. Als Beispiel nehmen wir die Polynomfunktion mit dem Funktionsterm
Die Abbildung zeigt den Verlauf der Graphen von , und .
Horizontale Tangenten
Besitzt eine Funktion mit an einer Stelle ihren größten Wert, gilt also für alle dieses Intervalls , und ist an der Stelle differenzierbar, so kann die Ableitung dort nur gleich Null sein: . Eine entsprechende Aussage gilt, falls in den kleinsten Wert annimmt.
Geometrische Deutung dieses Satzes von Fermat ist, dass der Graph der Funktion in lokalen Extrempunkten eine parallel zur -Achse verlaufende Tangente, auch waagerechte Tangente genannt, besitzt.
Es ist somit für differenzierbare Funktionen eine notwendige Bedingung für das Vorliegen einer Extremstelle, dass die Ableitung an der betreffenden Stelle den Wert 0 annimmt:
Umgekehrt kann aber daraus, dass die Ableitung an einer Stelle den Wert Null hat, noch nicht auf eine Extremstelle geschlossen werden, es könnte auch beispielsweise ein Sattelpunkt vorliegen. Eine Liste verschiedener hinreichender Kriterien, deren Erfüllung sicher auf eine Extremstelle schließen lässt, findet sich im Artikel Extremwert. Diese Kriterien benutzen meist die zweite oder noch höhere Ableitungen.
Bedingung im Beispiel
Im Beispiel ist
Daraus folgt, dass genau für und gilt. Die Funktionswerte an diesen Stellen sind und , d. h., die Kurve hat in den Punkten und waagerechte Tangenten, und nur in diesen.
Da die Folge
abwechselnd aus kleinen und großen Werten besteht, muss in diesem Bereich ein Hoch- und ein Tiefpunkt liegen. Nach dem Satz von Fermat hat die Kurve in diesen Punkten eine waagerechte Tangente, es kommen also nur die oben ermittelten Punkte in Frage: Also ist ein Hochpunkt und ein Tiefpunkt.
Kurvendiskussion
Mit Hilfe der Ableitungen lassen sich noch weitere Eigenschaften der Funktion analysieren, wie die Existenz von Wende- und Sattelpunkten, die Konvexität oder die oben schon angesprochene Monotonie. Die Durchführung dieser Untersuchungen ist Gegenstand der Kurvendiskussion.
Termumformungen
Neben der Bestimmung der Steigung von Funktionen ist die Differentialrechnung durch ihren Kalkül ein wesentliches Hilfsmittel bei der Termumformung. Hierbei löst man sich von jeglichem Zusammenhang mit der ursprünglichen Bedeutung der Ableitung als Anstieg. Hat man zwei Terme als gleich erkannt, lassen sich durch Differentiation daraus weitere (gesuchte) Identitäten gewinnen. Ein Beispiel mag dies verdeutlichen:
Aus der bekannten Partialsumme
der geometrischen Reihe soll die Summe
berechnet werden. Dies gelingt durch Differentiation mit Hilfe der Quotientenregel:
Alternativ ergibt sich die Identität auch durch Ausmultiplizieren und anschließendes dreifaches Teleskopieren, was aber nicht so einfach zu durchschauen ist.
Zentrale Aussagen der Differentialrechnung einer Variablen
Fundamentalsatz der Analysis
Die wesentliche Leistung Leibniz’ war die Erkenntnis, dass Integration und Differentiation zusammenhängen. Diese formulierte er im Hauptsatz der Differential- und Integralrechnung, auch Fundamentalsatz der Analysis genannt, der besagt:
Ist ein Intervall, eine stetige Funktion und eine beliebige Zahl aus , so ist die Funktion
stetig differenzierbar, und ihre Ableitung ist gleich .
Hiermit ist also eine Anleitung zum Integrieren gegeben: Gesucht ist eine Funktion , deren Ableitung der Integrand ist. Dann gilt:[43]
Mittelwertsatz der Differentialrechnung
Ein weiterer zentraler Satz der Differentialrechnung ist der Mittelwertsatz, der 1821 von Cauchy bewiesen wurde.[44]
Es sei eine Funktion, die auf dem abgeschlossenen Intervall (mit ) definiert und stetig ist. Außerdem sei die Funktion im offenen Intervall differenzierbar. Unter diesen Voraussetzungen gibt es mindestens ein , sodass
gilt – geometrisch-anschaulich: Zwischen zwei Schnittpunkten einer Sekante gibt es auf der Kurve einen Punkt mit zur Sekante paralleler Tangente.[45]
Monotonie und Differenzierbarkeit
Ist und eine differenzierbare Funktion mit für alle , so gelten folgende Aussagen:[46]
- Die Funktion ist strikt monoton.
- Es ist mit irgendwelchen .
- Die Umkehrfunktion existiert, ist differenzierbar und erfüllt .
Daraus lässt sich herleiten, dass eine stetig differenzierbare Funktion , deren Ableitung nirgends verschwindet, bereits einen Diffeomorphismus zwischen den Intervallen und definiert. In mehreren Variablen ist die analoge Aussage falsch. So verschwindet die Ableitung der komplexen Exponentialfunktion , nämlich sie selbst, in keinem Punkt, aber es handelt sich um keine (global) injektive Abbildung . Man beachte, dass diese als höherdimensionale reelle Funktion aufgefasst werden kann, da ein zweidimensionaler -Vektorraum ist.
Allerdings liefert der Satz von Hadamard ein Kriterium, mit dem in manchen Fällen gezeigt werden kann, dass eine stetig differenzierbare Funktion ein Homöomorphismus ist.
Die Regel von de L’Hospital
Als eine Anwendung des Mittelwertsatzes lässt sich eine Beziehung herleiten, die es in manchen Fällen erlaubt, unbestimmte Terme der Gestalt oder zu berechnen.[47]
Seien differenzierbar und habe keine Nullstelle. Ferner gelte entweder
oder
- .
Dann gilt
unter der Bedingung, dass der letzte Grenzwert in existiert.
Differentialrechnung bei Funktionenfolgen und Integralen
In vielen analytischen Anwendungen hat man es nicht mit einer Funktion , sondern mit einer Folge zu tun. Dabei muss geklärt werden, inwieweit sich der Ableitungsoperator mit Prozessen wie Grenzwerten, Summen oder Integralen verträgt.
Grenzfunktionen
Bei einer konvergenten, differenzierbaren Funktionenfolge ist es im Allgemeinen nicht möglich, Rückschlüsse auf den Grenzwert der Folge zu ziehen, selbst dann nicht, wenn gleichmäßig konvergiert. Die analoge Aussage in der Integralrechnung ist hingegen richtig: Bei gleichmäßiger Konvergenz können Limes und Integral vertauscht werden, zumindest dann, wenn die Grenzfunktion „gutartig“ ist.
Aus dieser Tatsache kann zumindest Folgendes geschlossen werden: Sei eine Folge stetig differenzierbarer Funktionen, sodass die Folge der Ableitungen gleichmäßig gegen eine Funktion konvergiert. Es gelte außerdem, dass die Folge für mindestens einen Punkt konvergiert. Dann konvergiert bereits gleichmäßig gegen eine differenzierbare Funktion und es gilt .[48]
Vertauschen mit unendlichen Reihen
Sei eine Folge stetig differenzierbarer Funktionen, sodass die Reihe konvergiert, wobei die Supremumsnorm bezeichnet. Konvergiert außerdem die Reihe für ein , dann konvergiert die Funktionenreihe gleichmäßig gegen eine differenzierbare Funktion, und es gilt[49]
Das Resultat geht auf Karl Weierstraß zurück.[50]
Vertauschen mit Integration
Es sei eine stetige Funktion, sodass die partielle Ableitung
existiert und stetig ist. Dann ist auch
differenzierbar, und es gilt
Diese Regel wird auch als Leibnizsche Regel bezeichnet.[51]
Differentialrechnung über den komplexen Zahlen
Bisher wurde nur von reellen Funktionen gesprochen. Alle behandelten Regeln lassen sich jedoch auf Funktionen mit komplexen Eingaben und Werten übertragen. Dies hat den Hintergrund, dass die komplexen Zahlen genau wie die reellen Zahlen einen Körper bilden, dort also Addition, Multiplikation und Division erklärt ist. Diese zusätzliche Struktur bildet den entscheidenden Unterschied zu einer Herangehensweise mehrdimensionaler reeller Ableitungen, wenn bloß als zweidimensionaler -Vektorraum aufgefasst wird. Ferner lassen sich die euklidischen Abstandsbegriffe der reellen Zahlen (siehe auch Euklidischer Raum) auf natürliche Weise auf komplexe Zahlen übertragen. Dies erlaubt eine analoge Definition und Behandlung der für die Differentialrechnung wichtigen Begriffe wie Folge und Grenzwert.[52]
Ist also offen, eine komplexwertige Funktion, so heißt an der Stelle komplex differenzierbar, wenn der Grenzwert
existiert.[53] Dieser wird mit bezeichnet und (komplexe) Ableitung von an der Stelle genannt. Es ist demnach möglich, den Begriff der Linearisierung ins Komplexe weiterzutragen: Die Ableitung ist die „Steigung“ der linearen Funktion, die bei optimal approximiert. Allerdings ist darauf zu achten, dass der Wert im Grenzwert nicht nur reelle, sondern auch komplexe Zahlen (nahe bei 0) annehmen kann. Dies hat zur Folge, dass der Terminus der komplexen Differenzierbarkeit wesentlich restriktiver ist als jener der reellen Differenzierbarkeit. Während im Reellen nur zwei Richtungen im Differenzenquotienten betrachtet werden mussten, sind es im Komplexen unendlich viele Richtungen, da diese keine Gerade, sondern eine Ebene aufspannen. So ist beispielsweise die Betragsfunktion nirgends komplex differenzierbar. Eine komplexe Funktion ist genau dann komplex differenzierbar in einem Punkt, wenn sie dort die Cauchy-Riemannschen Differentialgleichungen erfüllt und total differenzierbar ist.[54]
Trotz (bzw. gerade wegen) des viel einschränkenderen Begriffs der komplexen Differenzierbarkeit übertragen sich alle üblichen Rechenregeln der reellen Differentialrechnung in die komplexe Differentialrechnung. Dazu gehören die Ableitungsregeln, also zum Beispiel Summen-, Produkt- und Kettenregel, wie auch die Umkehrregel für inverse Funktionen. Viele Funktionen, wie Potenzen, die Exponentialfunktion oder der Logarithmus, haben natürliche Fortsetzungen in die komplexen Zahlen und besitzen weiterhin ihre charakteristischen Eigenschaften. Von diesem Gesichtspunkt her ist die komplexe Differentialrechnung mit ihrem reellen Analogon identisch.
Wenn eine Funktion in ganz komplex differenzierbar ist, nennt man sie auch eine in holomorphe Funktion.[55] Holomorphe Funktionen haben bedeutende Eigenschaften. So ist zum Beispiel jede holomorphe Funktion bereits (in jedem Punkt) beliebig oft differenzierbar. Die daraus aufkommende Klassifizierungfrage holomorpher Funktionen ist Gegenstand der Funktionentheorie. Es stellt sich heraus, dass im komplex-eindimensionalen Fall der Begriff holomorph äquivalent zum Begriff analytisch ist. Demnach ist jede holomorphe Funktion analytisch, und umgekehrt. Ist eine Funktion sogar in ganz holomorph, so nennt man sie ganz. Beispiele für ganze Funktionen sind die Potenzfunktionen mit natürlichen Zahlen sowie , und .
Differentialrechnung mehrdimensionaler Funktionen
Alle vorherigen Ausführungen legten eine Funktion in einer Variablen (also mit einer reellen oder komplexen Zahl als Argument) zugrunde. Funktionen, die Vektoren auf Vektoren oder Vektoren auf Zahlen abbilden, können ebenfalls eine Ableitung haben. Allerdings ist eine Tangente an den Funktionsgraph in diesen Fällen nicht mehr eindeutig bestimmt, da es viele verschiedene Richtungen gibt. Hier ist also eine Erweiterung des bisherigen Ableitungsbegriffs notwendig.
Mehrdimensionale Differenzierbarkeit und die Jacobi-Matrix
Richtungsableitung
Es sei offen, eine Funktion, und ein (Richtungs-)Vektor. Aufgrund der Offenheit von gibt es ein mit für alle , weshalb die Funktion mit wohldefiniert ist. Ist diese Funktion in differenzierbar, so heißt ihre Ableitung Richtungsableitung von an der Stelle in der Richtung und wird meistens mit bezeichnet.[56] Es gilt:
Es besteht ein Zusammenhang zwischen der Richtungsableitung und der Jacobi-Matrix. Ist differenzierbar, dann existiert und es gilt in einer Umgebung von :
wobei die Schreibweise das entsprechende Landau-Symbol bezeichnet.[57]
Es werde als Beispiel eine Funktion betrachtet, also ein Skalarfeld. Diese könnte eine Temperaturfunktion sein: In Abhängigkeit vom Ort wird die Temperatur im Zimmer gemessen, um zu beurteilen, wie effektiv die Heizung ist. Wird das Thermometer in eine bestimmte Raumrichtung bewegt, ist eine Veränderung der Temperatur festzustellen. Dies entspricht genau der entsprechenden Richtungsableitung.
Partielle Ableitungen
Die Richtungsableitungen in spezielle Richtungen , nämlich in die der Koordinatenachsen mit der Länge , nennt man die partiellen Ableitungen.
Insgesamt lassen sich für eine Funktion in Variablen partielle Ableitungen errechnen:[58]
Die einzelnen partiellen Ableitungen einer Funktion lassen sich auch gebündelt als Gradient oder Nablavektor anschreiben:[59]
Meist wird der Gradient als Zeilenvektor (also „liegend“) geschrieben. In manchen Anwendungen, besonders in der Physik, ist jedoch auch die Schreibweise als Spaltenvektor (also „stehend“) üblich. Partielle Ableitungen können selbst differenzierbar sein und ihre partiellen Ableitungen lassen sich dann in der sogenannten Hesse-Matrix anordnen.
Totale Differenzierbarkeit
Eine Funktion mit , wobei eine offene Menge ist, heißt in einem Punkt total differenzierbar (oder auch nur differenzierbar, manchmal auch Fréchet-differenzierbar[56]), falls eine lineare Abbildung existiert, sodass
gilt.[60] Für den eindimensionalen Fall stimmt diese Definition mit der oben angegebenen überein. Die lineare Abbildung ist bei Existenz eindeutig bestimmt, ist also insbesondere unabhängig von der Wahl äquivalenter Normen. Die Tangente wird daher durch die lokale Linearisierung der Funktion abstrahiert. Die Matrixdarstellung der ersten Ableitung von nennt man Jacobi-Matrix. Es handelt sich um eine -Matrix. Für erhält man den weiter oben beschriebenen Gradienten.
Zwischen den partiellen Ableitungen und der totalen Ableitung besteht folgender Zusammenhang: Existiert in einem Punkt die totale Ableitung, so existieren dort auch alle partiellen Ableitungen. In diesem Fall stimmen die partiellen Ableitungen mit den Koeffizienten der Jacobi-Matrix überein:
Umgekehrt folgt aus der Existenz der partiellen Ableitungen in einem Punkt nicht zwingend die totale Differenzierbarkeit, ja nicht einmal die Stetigkeit. Sind die partiellen Ableitungen jedoch zusätzlich in einer Umgebung von stetig, dann ist die Funktion in auch total differenzierbar.[61]
Rechenregeln der mehrdimensionalen Differentialrechnung
Kettenregel
Es seien und offen sowie und in bzw. differenzierbar, wobei . Dann ist mit in differenzierbar mit Jacobi-Matrix
Mit anderen Worten, die Jacobi-Matrix der Komposition ist das Produkt der Jacobi-Matrizen von und .[62] Es ist zu beachten, dass die Reihenfolge der Faktoren im Gegensatz zum klassischen eindimensionalen Fall eine Rolle spielt.
Produktregel
Mit Hilfe der Kettenregel kann die Produktregel auf reellwertige Funktionen mit höherdimensionalem Definitionsbereich verallgemeinert werden.[63] Ist offen und sind beide in differenzierbar, so folgt
oder in der Gradientenschreibweise
Funktionenfolgen
Sei offen. Es bezeichne eine Folge stetig differenzierbarer Funktionen , sodass es Funktionen und gibt (dabei ist der Raum der linearen Abbildungen von nach ), sodass Folgendes gilt:
- konvergiert punktweise gegen ,
- konvergiert lokal gleichmäßig gegen .
Dann ist stetig differenzierbar auf und es gilt .[64]
Implizite Differentiation
Ist eine Funktion durch eine implizite Gleichung gegeben, so folgt aus der mehrdimensionalen Kettenregel, die für Funktionen mehrerer Variablen gilt,
Für die Ableitung der Funktion ergibt sich daher
mit und
Zentrale Sätze der Differentialrechnung mehrerer Veränderlicher
Satz von Schwarz
Die Differentiationsreihenfolge ist bei der Berechnung partieller Ableitungen höherer Ordnung unerheblich, wenn alle partiellen Ableitungen bis zu dieser Ordnung (einschließlich) stetig sind. Dies bedeutet konkret: Ist offen und die Funktion zweimal stetig differenzierbar (d. h., alle zweifachen partiellen Ableitungen existieren und sind stetig), so gilt für alle und :
Der Satz wird falsch, wenn die Stetigkeit der zweifachen partiellen Ableitungen weggelassen wird.[65]
Satz von der impliziten Funktion
Der Satz von der impliziten Funktion besagt, dass Funktionsgleichungen auflösbar sind, falls die Jacobi-Matrix bezüglich bestimmter Variablen lokal invertierbar ist.[66]
Mittelwertsatz
Über den höherdimensionalen Mittelwertsatz gelingt es, eine Funktion entlang einer Verbindungsstrecke abzuschätzen, wenn die dortigen Ableitungen bekannt sind. Seien offen und differenzierbar. Gegeben seien zudem zwei Punkte , sodass die Verbindungsstrecke eine Teilmenge von ist. Dann postuliert der Mittelwertsatz die Ungleichung:[67]
Eine präzisere Aussage ist indes für den Fall reellwertiger Funktionen in mehreren Veränderlichen möglich, siehe auch Mittelwertsatz für reellwertige Funktionen mehrerer Variablen.
Höhere Ableitungen im Mehrdimensionalen
Auch im Fall höherdimensionaler Funktionen können höhere Ableitungen betrachtet werden. Die Konzepte haben jedoch einige starke Unterschiede zum klassischen Fall, die besonders im Falle mehrerer Veränderlicher in Erscheinung treten. Bereits die Jacobi-Matrix lässt erkennen, dass die Ableitung einer höherdimensionalen Funktion an einer Stelle nicht mehr die gleiche Gestalt wie der dortige Funktionswert haben muss. Wird nun die erste Ableitung erneut abgeleitet, so ist die erneute „Jacobi-Matrix“ im Allgemeinen ein noch umfangreicheres Objekt. Für dessen Beschreibung ist das Konzept der multilinearen Abbildungen bzw. des Tensors erforderlich. Ist , so ordnet jedem Punkt eine -Matrix (lineare Abbildung von nach ) zu. Induktiv definiert man für die höheren Ableitungen
wobei der Raum der -multilinearen Abbildungen von nach bezeichnet. Analog wie im eindimensionalen Fall definiert man die Räume der -mal stetig differenzierbaren Funktionen auf durch , und die glatten Funktion via[68]
Auch die Konzepte der Taylor-Formeln und der Taylorreihe lassen sich auf den höherdimensionalen Fall verallgemeinern, siehe auch Taylor-Formel im Mehrdimensionalen bzw. mehrdimensionale Taylorreihe.
Anwendungen
Fehlerrechnung
Ein Anwendungsbeispiel der Differentialrechnung mehrerer Veränderlicher betrifft die Fehlerrechnung, zum Beispiel im Kontext der Experimentalphysik. Während man im einfachsten Falle die zu bestimmende Größe direkt messen kann, wird es meistens der Fall sein, dass sie sich durch einen funktionalen Zusammenhang aus einfacher zu messenden Größen ergibt. Typischerweise hat jede Messung eine gewisse Unsicherheit, die man durch Angabe des Messfehlers zu quantifizieren versucht.[69]
Bezeichnet zum Beispiel mit das Volumen eines Quaders, so könnte das Ergebnis experimentell ermittelt werden, indem man Länge , Breite und Höhe einzeln misst. Treten bei diesen die Fehler , und auf, so gilt für den Fehler in der Volumenberechnung:
Allgemein gilt, dass wenn eine zu messende Größe funktional von einzeln gemessenen Größen durch abhängt und bei deren Messungen jeweils die Fehler entstehen, der Fehler der daraus errechneten Größe ungefähr bei
liegen wird. Dabei bezeichnet der Vektor die exakten Terme der einzelnen Messungen.[69]
Lösungsnäherung von Gleichungssystemen
Viele höhere Gleichungssysteme lassen sich nicht algebraisch geschlossen lösen. In manchen Fällen kann man aber zumindest eine ungefähre Lösung ermitteln. Ist das System durch gegeben, mit einer stetig differenzierbaren Funktion , so konvergiert die Iterationsvorschrift
unter gewissen Voraussetzungen gegen eine Nullstelle. Dabei bezeichnet das Inverse der Jacobi-Matrix zu . Der Prozess stellt eine Verallgemeinerung des klassischen eindimensionalen Newton-Verfahrens dar. Aufwendig ist allerdings die Berechnung dieser Inversen in jedem Schritt. Unter Verschlechterung der Konvergenzrate kann in manchen Fällen die Modifikation statt vorgenommen werden, womit nur eine Matrix invertiert werden muss.[70]
Extremwertaufgaben
Auch für die Kurvendiskussion von Funktionen ist die Auffindung von Minima bzw. Maxima, zusammengefasst Extrema, ein wesentliches Anliegen. Die mehrdimensionale Differentialrechnung liefert Möglichkeiten, diese zu bestimmen, sofern die betrachtete Funktion zweimal stetig differenzierbar ist. Analog zum Eindimensionalen besagt die notwendige Bedingung für die Existenz für Extrema, dass im besagten Punkt alle partiellen Ableitungen 0 sein müssen, also
für alle . Dieses Kriterium ist nicht hinreichend, dient aber dazu, diese kritischen Punkte als mögliche Kandidaten für Extrema zu ermitteln. Unter Bestimmung der Hesse-Matrix, der zweiten Ableitung, kann anschließend in manchen Fällen entschieden werden, um welche Art Extremstelle es sich handelt.[71] Im Gegensatz zum Eindimensionalen ist die Formenvielfalt kritischer Punkte größer. Mittels einer Hauptachsentransformation, also einer detaillierten Untersuchung der Eigenwerte, der durch eine mehrdimensionale Taylor-Entwicklung im betrachteten Punkt gegebenen quadratischen Form lassen sich die verschiedenen Fälle klassifizieren.[72]
Optimierung unter Nebenbedingungen
Häufig ist bei Optimierungsproblemen die Zielfunktion lediglich auf einer Teilmenge zu minimieren, wobei durch sog. Nebenbedingungen bzw. Restriktionen bestimmt ist. Ein Verfahren, das zur Lösung solcher Probleme herangezogen werden kann, ist die Lagrangesche Multiplikatorregel.[73] Diese nutzt die mehrdimensionale Differentialrechnung und lässt sich sogar auf Ungleichungsnebenbedingungen ausweiten.[74]
Beispiel aus der Mikroökonomie

In der Mikroökonomie werden beispielsweise verschiedene Arten von Produktionsfunktionen analysiert, um daraus Erkenntnisse für makroökonomische Zusammenhänge zu gewinnen. Hier ist vor allem das typische Verhalten einer Produktionsfunktion von Interesse: Wie reagiert die abhängige Variable Output (z. B. Output einer Volkswirtschaft), wenn die Inputfaktoren (hier: Arbeit und Kapital) um eine infinitesimal kleine Einheit erhöht werden?
Ein Grundtyp einer Produktionsfunktion ist etwa die neoklassische Produktionsfunktion. Sie zeichnet sich unter anderem dadurch aus, dass der Output bei jedem zusätzlichen Input steigt, dass aber die Zuwächse abnehmend sind. Es sei beispielsweise für eine Volkswirtschaft die Cobb-Douglas-Funktion
- mit
maßgebend. Zu jedem Zeitpunkt wird in der Volkswirtschaft unter dem Einsatz der Produktionsfaktoren Arbeit und Kapital mithilfe eines gegebenen Technologielevels Output produziert. Die erste Ableitung dieser Funktion nach den Produktionsfaktoren ergibt:
- .
Da die partiellen Ableitungen aufgrund der Beschränkung nur positiv werden können, sieht man, dass der Output bei einer Erhöhung der jeweiligen Inputfaktoren steigt. Die partiellen Ableitungen 2. Ordnung ergeben:
- .
Sie werden für alle Inputs negativ sein, also fallen die Zuwachsraten. Man könnte also sagen, dass bei steigendem Input der Output unterproportional steigt. Die relative Änderung des Outputs im Verhältnis zu einer relativen Änderung des Inputs ist hier durch die Elastizität gegeben. Vorliegend bezeichnet die Produktionselastizität des Kapitals, die bei dieser Produktionsfunktion dem Exponenten entspricht, der wiederum die Kapitaleinkommensquote repräsentiert. Folglich steigt der Output bei einer infinitesimal kleinen Erhöhung des Kapitals um die Kapitaleinkommensquote.
Weiterführende Theorien
Differentialgleichungen
Eine wichtige Anwendung der Differentialrechnung besteht in der mathematischen Modellierung physikalischer Vorgänge. Wachstum, Bewegung oder Kräfte haben alle mit Ableitungen zu tun, ihre formelhafte Beschreibung muss also Differentiale enthalten. Typischerweise führt dies auf Gleichungen, in denen Ableitungen einer unbekannten Funktion auftauchen, sogenannte Differentialgleichungen.
Beispielsweise verknüpft das newtonsche Bewegungsgesetz
die Beschleunigung eines Körpers mit seiner Masse und der auf ihn einwirkenden Kraft . Das Grundproblem der Mechanik lautet deshalb, aus einer gegebenen Beschleunigung die Ortsfunktion eines Körpers herzuleiten. Diese Aufgabe, eine Umkehrung der zweifachen Differentiation, hat die mathematische Gestalt einer Differentialgleichung zweiter Ordnung. Die mathematische Schwierigkeit dieses Problems rührt daher, dass Ort, Geschwindigkeit und Beschleunigung Vektoren sind, die im Allgemeinen nicht in die gleiche Richtung zeigen, und dass die Kraft von der Zeit und vom Ort abhängen kann.
Da viele Modelle mehrdimensional sind, sind bei der Formulierung häufig die weiter oben erklärten partiellen Ableitungen sehr wichtig, mit denen sich partielle Differentialgleichungen formulieren lassen. Mathematisch kompakt werden diese mittels Differentialoperatoren beschrieben und analysiert.
Differentialgeometrie
Zentrales Thema der Differentialgeometrie ist die Ausdehnung der klassischen Analysis auf höhere geometrische Objekte. Diese sehen lokal so aus wie zum Beispiel der euklidische Raum , können aber global eine andere Gestalt haben. Der Begriff hinter diesem Phänomen ist die Mannigfaltigkeit. Mit Hilfe der Differentialgeometrie werden Fragestellungen über die Natur solcher Objekte studiert – zentrales Werkzeug ist weiterhin die Differentialrechnung. Gegenstand der Untersuchung sind oftmals die Abstände zwischen Punkten oder die Volumina von Figuren. Beispielsweise kann mit ihrer Hilfe der kürzestmögliche Weg zwischen zwei Punkten auf einer gekrümmten Fläche bestimmt und gemessen werden, die sogenannte Geodätische. Für die Messung von Volumina wird der Begriff der Differentialform benötigt. Differentialformen erlauben unter anderem eine koordinatenunabhängige Integration.
Sowohl die theoretischen Ergebnisse als auch Methoden der Differentialgeometrie haben bedeutende Anwendungen in der Physik. So beschrieb Albert Einstein seine Relativitätstheorie mit differentialgeometrischen Begriffen.
Verallgemeinerungen
In vielen Anwendungen ist es wünschenswert, Ableitungen auch für stetige oder sogar unstetige Funktionen bilden zu können. So kann beispielsweise eine sich am Strand brechende Welle durch eine partielle Differentialgleichung modelliert werden, die Funktion der Höhe der Welle ist aber noch nicht einmal stetig. Zu diesem Zweck verallgemeinerte man Mitte des 20. Jahrhunderts den Ableitungsbegriff auf den Raum der Distributionen und definierte dort eine schwache Ableitung. Eng verbunden damit ist der Begriff des Sobolew-Raums.
Der Begriff der Ableitung als Linearisierung lässt sich analog auf Funktionen zwischen zwei normierbaren topologischen Vektorräumen und übertragen (s. Hauptartikel Fréchet-Ableitung, Gâteaux-Differential, Lorch-Ableitung): heißt in Fréchet-differenzierbar, wenn ein stetiger linearer Operator existiert, sodass
- .
Eine Übertragung des Begriffes der Ableitung auf andere Ringe als und (und Algebren darüber) führt zur Derivation.
Siehe auch
Literatur
Differentialrechnung ist ein zentraler Unterrichtsgegenstand in der Sekundarstufe II und wird somit in allen Mathematik-Lehrbüchern dieser Stufe behandelt.
Lehrbücher für Mathematik-Studierende
- Henri Cartan: Differentialrechnung. Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01442-3.
- Henri Cartan: Differentialformen. Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01443-1.
- Henri Cartan: Elementare Theorien der analytischen Funktionen einer und mehrerer komplexen Veränderlichen. Bibliographisches Institut, Mannheim 1966, 1981, ISBN 3-411-00112-7.
- Richard Courant: Vorlesungen über Differential- und Integralrechnung. 2 Bände. Springer 1928, 4. Auflage 1971, ISBN 3-540-02956-7.
- Jean Dieudonné: Grundzüge der modernen Analysis. Band 1. Vieweg, Braunschweig 1972, ISBN 3-528-18290-3.
- Gregor M. Fichtenholz: Differential- und Integralrechnung I–III. Verlag Harri Deutsch, Frankfurt am Main 1990–2004, ISBN 978-3-8171-1418-4 (kompletter Satz).
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. 7. Auflage. Vieweg, Braunschweig 2004, ISBN 3-528-67224-2.
- Otto Forster: Analysis 2. Differentialrechnung im . Gewöhnliche Differentialgleichungen. 6. Auflage. Vieweg, Braunschweig 2005, ISBN 3-528-47231-6.
- Konrad Königsberger: Analysis. 2 Bände. Springer, Berlin 2004, ISBN 3-540-41282-4.
- Wladimir I. Smirnow: Lehrgang der höheren Mathematik (Teil 1–5). Verlag Harri Deutsch, Frankfurt am Main, 1995–2004, ISBN 978-3-8171-1419-1 (kompletter Satz).
- Steffen Timmann: Repetitorium der Analysis. 2 Bände. Binomi, Springe 1993, ISBN 3-923923-50-3, ISBN 3-923923-52-X.
- Serge Lang: A First Course in Calculus. Fifth Edition, Springer, ISBN 0-387-96201-8.
Lehrbücher für das Grundlagenfach Mathematik
- Rainer Ansorge, Hans Joachim Oberle: Mathematik für Ingenieure. Band 1. Akademie-Verlag, Berlin 1994, 3. Auflage 2000, ISBN 3-527-40309-4.
- Günter Bärwolff (unter Mitarbeit von G. Seifert): Höhere Mathematik für Naturwissenschaftler und Ingenieure. Elsevier Spektrum Akademischer Verlag, München 2006, ISBN 3-8274-1688-4.
- Lothar Papula: Mathematik für Naturwissenschaftler und Ingenieure. Band 1. Vieweg, Wiesbaden 2004, ISBN 3-528-44355-3.
- Klaus Weltner: Mathematik für Physiker 1. Springer, Berlin 2011, ISBN 978-3-642-15527-7.
- Peter Dörsam: Mathematik anschaulich dargestellt für Studierende der Wirtschaftswissenschaften. 15. Auflage. PD-Verlag, Heidenau 2010, ISBN 978-3-86707-015-7.
Weblinks
- Tool zur Bestimmung von Ableitungen beliebiger Funktionen mit einer oder mehreren Variablen mit Rechenweg (deutsch; benötigt JavaScript)
- Online-Rechner zum Ableiten von Funktionen mit Rechenweg und Erklärungen (deutsch)
- Anschauliche Erklärung von Ableitungen
- Beispiele zu jeder Ableitungsregel
Einzelnachweise
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 316.
- ↑ Serge Lang: A First Course in Calculus. Fifth Edition. Springer, S. 59–61.
- ↑ Fritz Wicke: Einführung in die Höhere Mathematik: unter besonderer Berücksichtigung der Bedürfnisse des Ingenieurs. Band 1. Springer, 1927, Seite 103.
- ↑ Carl Spitz: Erster Cursus der Differential- und Integralrechnung. C. F. Winter’sche Verlagshandlung, 1871, Seite 15
- ↑ Carl Spitz: Erster Cursus der Differential- und Integralrechnung. C. F. Winter’sche Verlagshandlung, 1871, Seite 16
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 422.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 170.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 292.
- ↑ Serge Lang: A First Course in Calculus. Fifth Edition. Springer, S. 463–464.
- ↑ John Stillwell: Mathematics and Its History, Third Edition, Springer, S. 192–194.
- ↑ Serge Lang: Calculus of Several Variables, Third Edition, Springer, S. 439.
- ↑ Serge Lang: Calculus of Several Variables, Third Edition, Springer, S. 434.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 161.
- ↑ Serge Lang: Calculus of Several Variables, Third Edition, Springer, S. 435–436.
- ↑ Hans Wußing, Heinz-Wilhelm Alten, Heiko Wesemüller-Kock, Eberhard Zeidler: 6000 Jahre Mathematik: Von den Anfängen bis Newton und Leibniz. Springer, 2008, S. 429.
- ↑ Thomas Sonar: 3000 Jahre Analysis, Springer, S. 247–248.
- ↑ Thomas Sonar: 3000 Jahre Analysis, Springer, S. 378.
- ↑ Marquis de L’Hospital: Analyse des Infiniment Petits pour l’Intelligence des Lignes Courbes. Preface, S. ix–x: « L’Étendue de ce calcul est immense: … »; archive.org.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Springer, S. 87.
- ↑ John Stillwell: Mathematics and its history, Third Edition, Springer, S. 157.
- ↑ Thomas Sonar: 3000 Jahre Analysis, Springer, S. 424–425.
- ↑ Hans Wußing, Heinz-Wilhelm Alten, Heiko Wesemüller-Kock, Eberhard Zeidler: 6000 Jahre Mathematik: Von Euler bis zur Gegenwart. Springer, 2008, S. 233.
- ↑ Thomas Sonar: 3000 Jahre Analysis, Springer, S. 506–514.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung, Springer, S. 91.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 284.
- ↑ Bronstein et al.: Taschenbuch der Mathematik, Verlag Harri Deutsch, S. 394.
- ↑ a b c Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 318.
- ↑ Jeremy Gray: The Real and the Complex: A History of Analysis in the 19th Century, Springer, S. 271–272.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 323.
- ↑ a b Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 324.
- ↑ Differentialrechnung. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung, Springer, S. 90.
- ↑ Harro Heuser: Lehrbuch der Analysis. Teubner, Wiesbaden 2003, ISBN 3-519-62233-5, S. 269.
- ↑ Thomas Sonar: 3000 Jahre Analysis, Springer, S. 408.
- ↑ Lokenath Debnath: The Legacy of Leonhard Euler – A Tricentennial Tribute, Imperial College Press, S. 26.
- ↑ Ali Mason: Advanced Differential Equations. EDTECH, 1019, ISBN 1-83947-389-4, S. 67.
- ↑ Karl Bosch: Mathematik für Wirtschaftswissenschaftler. 14. Auflage, Oldenbourg, 2003, S. 77
- ↑ Klaus Hefft: Mathematischer Vorkurs zum Studium der Physik. 2. Auflage. Springer, 2018, S. 97.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 329.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. S. 358.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 330–331.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 304.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 32–33.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung, Springer, S. 248.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 335.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 336.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 346.
- ↑ Terence Tao: Analysis II, Third Edition, Hindustan Book Agency, S. 64.
- ↑ Terence Tao: Analysis II, Third Edition, Hindustan Book Agency, S. 65.
- ↑ Jeremy Gray: The Real and the Complex: A History of Analysis in the 19th Century, Springer, S. 201.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 89.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 16 ff.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 35.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 42–43.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 45.
- ↑ a b Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 157.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 158.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 159.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 165.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 154–157.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 158–163.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 173.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 175.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 177.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 192.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 230–232.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 176.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2. Auflage. Birkhäuser, S. 188.
- ↑ a b T. Arens et al.: Mathematik. Spektrum, S. 794.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 803.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 811.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 812.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 1193–1195.
- ↑ T. Arens et al.: Mathematik. Spektrum, S. 1196.


























































































































































![{\displaystyle [x_{0},x_{0}+\Delta x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4c9fca7d2a7b17975192095def858d129b413b9)













































































































![{\displaystyle f(x)={\sqrt[{m}]{x}}=x^{\frac {1}{m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6cb473bb3eb4fc3708532fd9ecc490e04a2f264)

![{\displaystyle f'(x)={\frac {1}{m}}{\frac {f}{x}}={\frac {1}{m}}\;{\frac {\sqrt[{m}]{x}}{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17d3630d048bade9d78586f3079b59cdea97b1ea)














































































![{\displaystyle u[v(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecd0b3af2d9804a34ab0fd2dad5a66481163343d)






































































![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
























![{\displaystyle f_{n}\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b32ac944f464748dfb697057d3788497bfabb6fe)
![{\displaystyle f_{n}'\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa20a73b34f9d8b5ab0dd50731c0f34dcabbb59f)
![{\displaystyle g\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/38132af5ea7cd916293fe93f29187bd461a5e270)

![{\displaystyle x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06636653315ee7c3b5dc9bdb6ac3fb8cccadc145)


![{\displaystyle ||f_{n}'||_{\infty }:=\sup _{x\in [a,b]}|f_{n}'(x)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c15371c13ae76eca92cdd6495b526d331581d44c)



![{\displaystyle f\colon [a,b]\times [c,d]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d985fd7a6c6afcc39f2bfa732015f9c55ebf223)






































































































































