Geburts- und Todesprozess
Als Geburts- und Todesprozess bzw. als Geburts- und Sterbeprozess bezeichnet man in der Stochastik spezielle stochastische Prozesse, die zur Modellierung von Populationen oder in der Warteschlangentheorie benutzt werden können.
Definition
Ein Geburts- und Todesprozess ist ein homogener Markow-Prozess in stetiger Zeit mit Zustandsraum , bei dem aus einem Zustand nur Übergänge in den nächstgrößeren Zustand („Geburt“) oder, falls , in den nächstkleineren Zustand („Tod“) möglich sind. Die Übergangsraten sind dabei gegeben durch nichtnegative Zahlen und , die als Geburts- bzw. Sterberaten bezeichnet werden. Sind alle gleich null, so spricht man von einem reinen Geburtsprozess, sind alle gleich null, so spricht man von einem reinen Sterbe- bzw. Todesprozess.
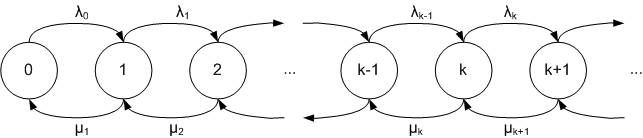
Aufgrund dieser starken Restriktionen an die Übergangswahrscheinlichkeiten stellen Geburts- und Todesprozesse wichtige Spezialfälle allgemeiner Markow-Ketten dar, bei denen vergleichsweise leicht Eigenschaften, wie Übergangswahrscheinlichkeiten oder das Langzeitverhalten, untersucht werden können.
Ein Geburts- und Todesprozess lässt sich als stochastisches Modell verstehen, in dem sich ein System zum Startzeitpunkt in einem bestimmten Zustand befindet (z. B. die Anzahl der Kaninchen einer Population). Nach einem gewissen zufälligen Zeitintervall geht das System dann in einen neuen Zustand über, wobei dafür je nach Zustand unterschiedliche Wahrscheinlichkeiten existieren. Geburts- und Todesprozesse zeichnen sich speziell dadurch aus, dass vom Zustand ausschließlich in die Zustände (entspricht der Geburt eines Kaninchens) und (entspricht dem Tod eines Kaninchens) übergegangen werden kann.
Eigenschaften
Die Eigenschaft eines Geburts- und Todesprozesses , ein Markow-Prozess zu sein, bedeutet, dass die zeitliche Entwicklung der Zustände nur vom aktuellen Zustand abhängt, aber nicht von davorliegenden Zuständen mit , der Prozess ist sozusagen gedächtnislos. Hieraus folgt, dass die zufällige Verweildauer in jedem Zustand exponentialverteilt ist. Der Erwartungswert dieser Verweilzeit im Zustand ist gegeben durch . Wenn der Prozess nach dieser Zeit springt, geht er mit der Wahrscheinlichkeit in den Zustand und mit Wahrscheinlichkeit in den Zustand über.
Anwendungen
Geburts- und Todesprozesse werden in der Telekommunikation zur Modellierung des Verkehrsaufkommens verwendet. Beispielsweise hat ein Telekommunikationsanbieter 200 Leitungen. Jede Leitung kann von einem Anrufer belegt werden, indem er jemanden anruft. Nehmen wir an, dass das Anruferverhalten und die Anruflänge einem Poisson-Prozess folgt. Das heißt, die Zeit zwischen zwei Anrufen ist exponentiell verteilt, ebenso die Telefondauer. Zudem gilt: Falls alle 200 Leitungen belegt sind, kann kein weiterer Anrufer telefonieren – er wird blockiert. Der Telekommunikationsanbieter kann sich nun mit einem Geburts- und Sterbeprozess ein Modell aufstellen. Mit diesem Modell kann er dann zum Beispiel berechnen, wie hoch die Wahrscheinlichkeit ist, dass ein Anrufer nicht telefonieren kann. Dieser wird dann blockiert und ist unzufrieden.

- Die Zustände stehen in diesem Beispiel für die Anzahl der belegten Leitungen. Der Zustand 5 bedeutet zum Beispiel, dass gerade fünf Leute telefonieren.
- gibt an, mit welcher Rate man von einem Zustand in den nächsten wechselt – hier also, wenn ein weiterer Anrufer zu telefonieren beginnt.
- ist die Rate, mit der ein Anrufer das Gespräch beendet.
Der Zustand 200 bedeutet, dass alle Leitungen belegt sind. Falls noch ein Anrufer versucht zu telefonieren, wird er abgewiesen. Zustand 200 repräsentiert die Wahrscheinlichkeit, dass man blockiert wird. Wenn diese Wahrscheinlichkeit hoch ist, muss der Anbieter eventuell mehr Leitungen kaufen.
Bedingungen für Wiederkehr und Vergänglichkeit
Die Bedingungen für Wiederkehr und Vergänglichkeit wurden von Samuel Karlin and James McGregor.[1] festgelegt.
- Ein Geburts- und Todesprozess ist wiederkehrend dann und nur dann
- Ein Geburts- und Todesprozess ist ergodisch dann und nur dann
- Ein Geburts- und Todesprozess ist null-wiederkehrend (null-rekurrent) dann und nur dann
Die Bedingungen für Wiederkehr, Vergänglichkeit, Ergodizität und Null-Wiederkehr können in einer expliziteren Form hergeleitet werden.[2]
Für eine natürliche Zahl , lassen bezeichnen die te Iteration des natürlichen Logarithmus, d. h. , und für alle , .
Dann sind die Bedingungen für das Wiederauftreten und die Vergänglichkeit eines Geburts- und Todesprozesses wie folgt.
- Ein Geburts- und Todesprozess ist vergänglich, wenn es , und , so dass für alle
,
wobei die leere Summe für wird als 0 angenommen.
- Ein Geburts- und Todesprozess ist wiederkehrend, wenn es und , so dass für alle
,
Es können breitere Klassen von Geburts- und Sterbeprozessen definiert werden, für die die Bedingungen für Wiederkehr und Vergänglichkeit festgelegt sind.[3]
Anwendung
Wir betrachten die eindimensionale Irrfahrt , , die wie folgt definiert ist. Sei , und , , wobei die Werte annimmt und die Verteilung von definiert ist durchwobei die Koeffizienten die Bedingung für erfüllen. Die hier beschriebene Irrfahrt ist ein zeitdiskretes Analogon des Geburts- und Todesprozesses mit den Geburtenraten und den Sterberaten . Die Wiederkehr oder Vergänglichkeit der Irrfahrt ist also mit der Wiederkehr oder Vergänglichkeit des Geburts- und Todesprozesses verbunden.[2]
- Die Irrfahrt ist vergänglich, wenn es , und , so dass für alle ,
wobei die leere Summe für wird als 0 angenommen.
- Die Irrfahrt ist wiederkehrend, wenn es und , so dass für alle ,
Literatur
- Sören Asmussen: Applied Probability and Queues. 2. Auflage, Springer-Verlag, New-York 2003, ISBN 0-387-00211-1.
Weblinks
- Karl Grill: Theorie Stochastischer Prozesse (PDF, 211 KiB)
- H. Dinges: Stochastik für Informatiker (PostScript, 2,1 MiB)
Einzelnachweise
- ↑ Karlin, Samuel, McGregor, James: The classification of birth and death processes. In: Transactions of the American Mathematical Society. 86. Jahrgang, Nr. 2, 1957, S. 366–400, doi:10.1090/S0002-9947-1957-0094854-8 (ams.org [PDF]).
- ↑ a b Vyacheslav M. Abramov: Extension of the Bertrand–De Morgan test and its application. In: The American Mathematical Monthly. 127. Jahrgang, Nr. 5, 2020, S. 444–448, doi:10.1080/00029890.2020.1722551, arxiv:1901.05843 (tandfonline.com [PDF]).
- ↑ Vyacheslav M. Abramov: Necessary and sufficient conditions for the convergence of positive series. In: Journal of Classical Analysis. 19. Jahrgang, Nr. 2, 2022, S. 117–125, doi:10.7153/jca-2022-19-09, arxiv:2104.01702 (ele-math.com [PDF]).


























































