Geometrischer Schwerpunkt

Der geometrische Schwerpunkt oder Schwerpunkt einer geometrischen Figur (zum Beispiel Kreisbogen, Dreieck, Kegel) ist ein besonders ausgezeichneter Punkt, den man auch bei unsymmetrischen Figuren als eine Art Mittelpunkt interpretiert. Mathematisch entspricht dies der Mittelung aller Punkte innerhalb der Figur. Im Speziellen wird der geometrische Schwerpunkt von Linien auch Linienschwerpunkt, von Flächen Flächenschwerpunkt und von Körpern Volumenschwerpunkt genannt. Den Schwerpunkt kann man in einfachen Fällen durch geometrische Überlegungen erhalten, oder allgemein mit Mitteln der Mathematik durch Integration berechnen. Zur Beschreibung der Körper werden die Methoden der analytischen Geometrie verwendet. Der Schwerpunkt ist ein Gravizentrum.

Der geometrische Schwerpunkt entspricht dem Massenmittelpunkt eines physikalischen Körpers, der aus homogenem Material besteht, also überall die gleiche Dichte hat. Er lässt sich deshalb auch rein mechanisch durch Balancieren bestimmen. Diese Methode kann an Modellen angewandt werden, wenn es um geografische Mittelpunkte von Kontinenten oder Ländern geht (zum Beispiel Mittelpunkt Europas oder Mittelpunkt Deutschlands).

Insbesondere für die geografische Mitte wird mitunter auch eine andere Definition verwendet, nämlich der Ort der Halbierenden der jeweiligen Erstreckung in der geografischen Länge und in der geografischen Breite.^[1]

Bei konkav begrenzten Linien, Flächen (etwa einer sehr schlanken Mondsichel) oder Körpern (etwa dem Werkzeug Sichel) kann der Schwerpunkt, Mittelpunkt oder Mittenpunkt auch außerhalb des jeweiligen Objekts liegen.

Geometrischer Schwerpunkt endlich vieler Punkte im reellen Vektorraum

Sind in einem ${\displaystyle \mathbb {R} }$-Vektorraum ${\displaystyle {\mathcal {V}}}$ für eine natürliche Zahl ${\displaystyle m}$ paarweise verschiedene Punkte ${\displaystyle x_{1},\dots ,x_{m}\in {\mathcal {V}}}$ gegeben, so ist deren geometrischer Schwerpunkt ${\displaystyle s}$ definiert als

${\displaystyle s:={\frac {1}{m}}{\sum _{i=1}^{m}{x_{i}}}}$  .

In diesen Zusammenhang fällt der Begriff des Schwerpunkts eines ${\displaystyle k}$-dimensionalen Simplexes ${\displaystyle \Delta \subset \mathbb {R} ^{n}\;(k,n\in \mathbb {N} _{0})}$. Hat ein solches Simplex die Eckpunkte ${\displaystyle v_{0},\ldots ,v_{k}\in \mathbb {R} ^{n}}$, so ist sein Schwerpunkt ${\displaystyle s_{\Delta }}$ nichts weiter als der geometrische Schwerpunkt seiner Eckpunkte, also:

${\displaystyle s_{\Delta }={\frac {1}{k+1}}{\sum _{i=0}^{k}{v_{i}}}}$  .

Der Schwerpunkt eines solchen Simplexes zeichnet sich also dadurch aus, dass seine baryzentrischen Koordinaten in Bezug auf das Simplex alle gleich, nämlich

${\displaystyle ={\frac {1}{k+1}}}$

sind.^[2]

Bilden diese endlich vielen verschiedenen Punkte die Menge aller Eckpunkte einer geometrischen Figur im euklidischen Raum, so bezeichnet man den geometrischen Schwerpunkt all dieser auch als Eckenschwerpunkt der Figur.^[3] Beispiele hierfür geben insbesondere die Strecke, das Dreieck und das Tetraeder. Für Vierecke gilt nach Pierre de Varignon (1654–1722), dass der Eckenschwerpunkt eines Vierecks zugleich der Mittelpunkt der beiden Mittellinien, also der beiden Verbindungsstrecken gegenüberliegender Seitenmittelpunkte ist.^[4][5]

Schwerpunkte von elementargeometrischen Figuren

Im Folgenden werden einige Schwerpunkte elementargeometrischer Linien, Flächen und Körper angegeben und teilweise durch geometrische Überlegungen begründet.

Für achsensymmetrische oder rotationssymmetrische Figuren vereinfacht sich die Angabe des Schwerpunkts dadurch, dass dieser stets auf der Symmetrieachse liegt. Bei Figuren mit mehreren Symmetrieachsen bzw. punktsymmetrischen Objekten, wie beispielsweise bei einem Quadrat oder einem Kreis, liegt der Schwerpunkt im Schnittpunkt der Symmetrieachsen (Mittelpunkt) der Figur.

Linien

Strecke

Der geometrische Schwerpunkt einer Strecke liegt in deren Mitte, ist also identisch mit deren Mittelpunkt.

Kreisbogen

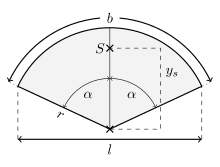
Ist der Ausschnitt des Kreises so gedreht und verschoben, dass die y-Achse des kartesischen Koordinatensystems eine Symmetrieachse des Kreisbogens ist und der Mittelpunkt des Kreises im Koordinatenursprung liegt (siehe Bild), dann lässt sich der Schwerpunkt durch

${\displaystyle x_{s}=0\quad y_{s}={\frac {2r^{2}\sin \alpha }{b}}=r{\frac {l}{b}}}$

berechnen.^[6] Hierbei ist ${\displaystyle r}$ der Radius des Kreises, ${\displaystyle b}$ die Länge des Kreisbogens und ${\displaystyle l}$ die Sehnenlänge des Kreisbogens.

${\displaystyle 0<\alpha \leq \pi }$

Für ${\displaystyle \alpha =0}$ versagt die Formel. Mit ${\displaystyle \lim _{\alpha \to 0}{\tfrac {l}{b}}=\cos \alpha }$ kann der Schwerpunkt auch für sehr kleine Winkel berechnet werden.

Musste der Kreis zu anfangs verschoben oder gedreht werden, dann muss zur Vervollständigung der Rechnung der berechnete Schwerpunkt entsprechend wieder zurückverschoben oder gedreht werden.

Flacher Bogen

Um den Schwerpunkt eines flachen Bogens näherungsweise zu berechnen, muss dieser im kartesischen Koordinatensystem so verschoben werden, dass der Mittelpunkt der Verbindungslinie der beiden Endpunkte im Koordinatenursprung liegt. Dann befindet sich der Schwerpunkt für ${\displaystyle h<r}$ in guter Näherung etwas unterhalb von

${\displaystyle z_{s}\approx {\frac {2h}{3}}}$.

Bei ${\displaystyle h=r}$ (Halbkreis) liegt der Schwerpunkt exakt bei ${\displaystyle {\frac {2r}{\pi }}}$. Die prozentuale Abweichung steigt in etwa proportional mit h und beträgt bei ${\displaystyle h=r}$ ungefähr 4,7 %. Daraus folgt der Ausdruck ${\displaystyle {\frac {2000h}{3(1000+47h/r)}}}$, der den Schwerpunkt im Bereich von ${\displaystyle (0\leq h\leq r)}$ mit einer Genauigkeit von besser als 5 Promille angibt. Die exakte Lage des Linienschwerpunktes ${\displaystyle z_{s}(h)}$ im gesamten Bereich von ${\displaystyle (0<h\leq 2r)}$ findet man mittels Einsetzen von ${\displaystyle \alpha =\arccos(1-h/r)}$ in die Formel für den auf den Kreismittelpunkt bezogenen Schwerpunkt ${\displaystyle r\sin(\alpha )/\alpha }$ (siehe Oberabschnitt Kreisbogen):

${\displaystyle z_{s}=h-r+{\frac {\sqrt {h(2r-h)}}{\arccos(1-h/r)}}}$.

Interessanterweise zeigt ${\displaystyle z_{s}}$ ein Maximum etwas größer als ${\displaystyle r}$ bei ${\displaystyle h\approx 1{,}9\ r}$. War zu Beginn eine Verschiebung oder Drehung notwendig, so muss der Schwerpunkt wieder entsprechend zurückverschoben werden.

Ebene Flächen

Bei ebenen Flächen lässt sich der Schwerpunkt allgemein dadurch ermitteln, dass man die ausgeschnittene Fläche an einem Punkt aufhängt und die Lotgerade, eine so genannte Schwerelinie einzeichnet. Der Schnittpunkt zweier Schwerelinien ist der Schwerpunkt. Alle weiteren Schwerelinien schneiden sich ebenfalls in diesem Schwerpunkt.
Bei Vielecken (insbesondere Dreiecken und Vierecken) unterscheidet man, je nach der Beschaffenheit der ebenen Fläche, zwischen drei verschiedenen Schwerpunkten:

Flächenschwerpunkt, Kantenschwerpunkt und Eckenschwerpunkt

wobei allerdings die beiden letztgenannten Schwerpunkte kaum eine praktische Anwendung haben und deshalb mehr oder weniger von nur akademischem Interesse sind.
Eine homogene Fläche von beliebiger, aber konstanter Dicke hat (genau gesagt) einen Flächenschwerpunkt; meist begnügt man sich jedoch mit der Bezeichnung Schwerpunkt.
Bei einem Vieleck, das nur aus seinen Umrandungen besteht (z. B. aus einzelnen dünnen Stangen oder in Form eines entsprechend gebogenen Drahtes), ist dessen Schwerpunkt ein Kantenschwerpunkt
Bei einem (fiktiven) Modell, bei dem die Masse des Körpers (des Vielecks) lediglich in den Ecken konzentriert ist (z. B. in Form von gleichschweren Kugeln), spricht man von einem Eckenschwerpunkt.
Die Lage dieser drei Schwerpunkte ist bei Vielecken mit gleicher äußerer Form, aber der o. g. unterschiedlichen Beschaffenheit, in der Regel voneinander verschieden; ihre Ermittlung richtet sich nach dem Einzelfall.

Dreieck

Eckenschwerpunkt

Sind die kartesischen Koordinaten der Eckpunkte des Dreiecks ${\displaystyle ABC}$ bekannt, so ergeben sich die Koordinaten des Eckenschwerpunkts ${\displaystyle S=(x_{s},y_{s})}$ als arithmetisches Mittel:

${\displaystyle x_{s}={\frac {1}{3}}(x_{A}+x_{B}+x_{C}),}$

${\displaystyle y_{s}={\frac {1}{3}}(y_{A}+y_{B}+y_{C})}$

Man rechnet nach, dass ${\displaystyle S}$ identisch ist mit dem gemeinsamen Punkt der Seitenhalbierenden des Dreiecks.

Da bei einem Dreieck der Eckenschwerpunkt mit dem Flächenschwerpunkt zusammenfällt (s. unten), spricht man einfach vom Schwerpunkt des Dreiecks.

Das Bild zeigt, wie man zeichnerisch den Schwerpunkt bestimmt.

Die normierten baryzentrischen Koordinaten von ${\displaystyle S}$ sind ${\displaystyle ({\tfrac {1}{3}}:{\tfrac {1}{3}}:{\tfrac {1}{3}})}$.

Ausgedrückt durch trilineare Koordinaten lautet der Eckenschwerpunkt eines Dreiecks mit Seitenlängen ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$

${\displaystyle \left({\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}\right)=(bc:ca:ab)\,.}$

Man kann den Schwerpunkt auch mit Hilfe der Länge einer Seite und der Höhe über der gleichen Seite, z. B. mit ${\displaystyle c}$ und ${\displaystyle h_{c}}$, in kartesischen Koordinaten bestimmen. Der Ursprung des Koordinatensystems liegt im Eckpunkt ${\displaystyle A}$ (siehe Abbildung). Auf diese Weise lassen sich die kartesischen Koordinaten des Schwerpunkts durch

${\displaystyle x_{s}={\frac {c+\xi }{3}},\quad y_{s}={\frac {h_{c}}{3}}}$

berechnen.^[7]

Der Schwerpunkt eines Dreiecks ist Mittelpunkt der Steiner-Ellipse (Steiner-Umellipse) und der Steiner-Inellipse.

Der Schwerpunkt eines Dreiecks ist zudem derjenige eindeutig bestimmte Punkt im Inneren des Dreiecks, dessen drei Verbindungsstrecken zu den Eckpunkten des Dreiecks dieses in drei Teildreiecke gleichen Flächeninhalts aufteilen (siehe baryzentrische Koordinaten).^[8][9]

Flächenschwerpunkt = Eckenschwerpunkt

Überdeckt man ein gegebenes Dreieck ${\displaystyle ABC}$ mit Rechtecken wie im Bild (wie bei der Einführung des bestimmten Integrals), so erkennt man mit Hilfe eines Strahlensatzes, dass die Schwerpunkte (Mittelpunkte) der Rechtecke alle auf der Seitenhalbierende ${\displaystyle CM_{c}}$ liegen. Damit liegt der Gesamtschwerpunkt aller Rechtecke auch auf dieser Seitenhalbierende. Verfeinert man nun die Rechtecküberdeckung, so bleibt die Eigenschaft auch bei unendlich feiner Überdeckung erhalten. Also gilt: der Flächenschwerpunkt des Dreiecks liegt auf der Seitenhalbierende ${\displaystyle CM_{c}}$. Mit analogen Überlegungen folgt schließlich:

Der Flächenschwerpunkt eines Dreiecks ist der gemeinsame Punkt der Seitenhalbierenden und damit gleich dem Eckenschwerpunkt.

Kantenschwerpunkt

Der Kantenschwerpunkt eines Dreiecks (oder auch: Der Schwerpunkt des Dreiecksumfangs) lässt sich auf einfache Weise geometrisch ermitteln – es ist dessen Spieker-Punkt.

Trapez

Der Schwerpunkt des Trapezes lässt sich folgendermaßen konstruieren: Eine Schwerelinie halbiert die beiden parallelen Seiten. Eine zweite erhält man, indem man die parallelen Seiten um die Länge der jeweils anderen in entgegengesetzten Richtungen verlängert, und die beiden Endpunkte miteinander verbindet. Die Formel in kartesischen Koordinaten lautet (gemessen vom linken unteren Eckpunkt):

${\displaystyle {\begin{aligned}x_{s}&={\frac {a^{2}-b^{2}+\xi (a+2b)}{3(a+b)}}\\y_{s}&={\frac {h}{3}}\cdot {\frac {a+2b}{a+b}}\end{aligned}}}$

Polygon

Der Schwerpunkt eines nicht überschlagenen, geschlossenen, auch unregelmäßigen Polygons mit N Eckpunkten kann wie folgt aus den kartesischen Koordinaten ${\displaystyle (x_{i},y_{i})}$ der Eckpunkte berechnet werden (der nullte Eckpunkt ${\displaystyle (x_{0},y_{0})}$ und der ${\displaystyle N}$-te Eckpunkt ${\displaystyle (x_{N},y_{N})}$ sind hierbei identisch). Die Eckpunkte werden fortlaufend gegen den Uhrzeigersinn durchnummeriert.^[10] Der Schwerpunkt eines regelmäßigen Polygons entspricht dem Mittelpunkt seines Umkreises.^[11]

Der Flächeninhalt ${\displaystyle A}$ des Polygons kann mit der Gaußschen Dreiecksformel

${\displaystyle A={\frac {1}{2}}\sum _{i=0}^{N-1}(x_{i}\ y_{i+1}-x_{i+1}\ y_{i})}$

bestimmt werden. Der Flächenschwerpunkt ${\displaystyle S}$ des Polygons wird dann mit den Formeln

${\displaystyle {\begin{aligned}x_{s}&={\frac {1}{6A}}\sum _{i=0}^{N-1}(x_{i}+x_{i+1})(x_{i}\ y_{i+1}-x_{i+1}\ y_{i})\\y_{s}&={\frac {1}{6A}}\sum _{i=0}^{N-1}(y_{i}+y_{i+1})(x_{i}\ y_{i+1}-x_{i+1}\ y_{i})\end{aligned}}}$

bestimmt.

Unregelmäßiges Viereck

Flächenschwerpunkt

Der Flächenschwerpunkt eines unregelmäßigen Vierecks (Bild 1) kann auch relativ einfach geometrisch bestimmt werden. Es gibt zwei Diagonalen in einem Viereck. Zuerst wird das Viereck mittels der ersten Diagonale ${\displaystyle {\overline {AC}}}$ in zwei gegenüberliegende Dreiecke ${\displaystyle \triangle {ACD}}$ und ${\displaystyle \triangle {ABC}}$ aufgeteilt und jeweils deren Flächenschwerpunkte ${\displaystyle S_{1}}$ und ${\displaystyle S_{3}}$ bestimmt. Geometrisch kann der Flächenschwerpunkt eines Dreiecks durch den Schnittpunkt seiner Seitenhalbierenden bestimmt werden. Die Verbindung der Flächenschwerpunkte dieser beiden Dreiecke bildet die Strecke ${\displaystyle {\overline {S_{1}S_{3}}}}$.

Dann wiederholt man die Prozedur mit den beiden Dreiecken ${\displaystyle \triangle {BCD}}$ und ${\displaystyle \triangle {ABD}}$ die durch die zweite Diagonale ${\displaystyle {\overline {BD}}}$ abgetrennt werden. Die Verbindung der Flächenschwerpunkte ${\displaystyle S_{2}}$ und ${\displaystyle S_{4}}$ dieser beiden neuen Dreiecke bildet die Strecke ${\displaystyle {\overline {S_{2}S_{4}}}}$. Der Schnittpunkt der Strecke ${\displaystyle {\overline {S_{1}S_{3}}}}$ und der Strecke ${\displaystyle {\overline {S_{2}S_{4}}}}$ ist der Flächenschwerpunkt ${\displaystyle S}$ des Vierecks ${\displaystyle ABCD}$.^[12][13]

Die Darstellung in Bild 2, konstruiert ähnlich wie oben beschrieben, beinhaltet auch eine alternative Vorgehensweise. Dazu sind in zwei sich kreuzenden Dreiecken deren Schwerpunkte ${\displaystyle S_{1}}$ und ${\displaystyle S_{2}}$ zu ermitteln. Abschließend wird eine Halbgerade ab ${\displaystyle S_{1}}$ parallel zur Diagonale ${\displaystyle {\overline {BD}}}$ und eine Halbgerade ab ${\displaystyle S_{2}}$ parallel zur Diagonale ${\displaystyle {\overline {AC}}}$ gezogen. Somit ist der Schnittpunkt der beiden Halbgeraden der Flächenschwerpunkt ${\displaystyle S}$ des Vierecks.

Ein möglicher elementarer geometrischer Beweis für die Korrektheit der Konstruktion mit der inkludierten Behauptung „${\displaystyle {\overline {S_{1}S_{3}}}}$ ist parallel zu ${\displaystyle {\overline {BD}}}$“ bzw. „${\displaystyle {\overline {S_{2}S_{4}}}}$ ist parallel zu ${\displaystyle {\overline {AC}}}$“ ist der Ansatz mithilfe ähnlicher Dreiecke, siehe Beweisskizze (Bild 3). Es genügt, wenn nur der Beweis für die Behauptung „${\displaystyle {\overline {S_{1}S_{3}}}}$ ist parallel zu ${\displaystyle {\overline {BD}}}$“ geführt wird.

• Die Dreiecke ${\displaystyle AS_{3}S_{1}}$ und ${\displaystyle AGF}$ sind ähnlich wegen ${\displaystyle {\overline {AS_{1}}}:{\overline {AF}}={\overline {AS_{3}}}:{\overline {AG}}\ (=2:3),}$

denn jede Schwerlinie wird vom Schwerpunkt im selben Verhältnis geteilt.

Somit gilt: ${\displaystyle S_{1}S_{3}\parallel FG}$.

• Die Dreiecke ${\displaystyle CFG}$ und ${\displaystyle CDB}$ sind ähnlich wegen ${\displaystyle {\overline {CF}}:{\overline {CD}}={\overline {CG}}:{\overline {CB}}\ (=1:2),}$

denn jede Schwerlinie verbindet eine Ecke mit dem Mittelpunkt der gegenüberliegenden Seite.

Somit gilt: ${\displaystyle FG\parallel BD.}$

• Aus beidem und der Transitivität der Parallelität folgt: ${\displaystyle S_{1}S_{3}}$ ist parallel zu ${\displaystyle {\overline {BD}}}$.

Was zu beweisen war.

Kreisausschnitt

Ist der Ausschnitt des Kreises so gedreht und verschoben, dass die y-Achse des kartesischen Koordinatensystems eine Symmetrieachse des Kreisausschnitts ist und der Mittelpunkt (des Vollkreises) im Ursprung liegt (siehe Bild), dann lässt sich der Schwerpunkt im Bogenmaß durch

${\displaystyle y_{s}={\frac {2r\sin \alpha }{3\alpha }}={\frac {2rl}{3b}}}$

mit ${\displaystyle 0<\alpha \leq \pi }$ berechnen.^[14]

Musste der Kreis anfangs verschoben oder gedreht werden, dann muss zur Vervollständigung der Rechnung der berechnete Schwerpunkt entsprechend wieder zurückverschoben oder gedreht werden.

Kreisabschnitt

Um den Flächenschwerpunkt eines Kreisabschnitts näherungsweise zu berechnen, muss dieser im kartesischen Koordinatensystem so verschoben werden, dass der Mittelpunkt der Verbindungslinie der beiden Endpunkte im Koordinatenursprung liegt. Dann befindet sich der Schwerpunkt für ${\displaystyle h<r}$ in guter Näherung etwas oberhalb von

${\displaystyle z_{s}\approx {\frac {2h}{5}}}$.

Bei ${\displaystyle h=r}$ (Halbkreis) liegt der Schwerpunkt exakt bei ${\displaystyle {\frac {4r}{3\pi }}}$. Die prozentuale Abweichung steigt in etwa proportional mit h und beträgt bei ${\displaystyle h=r}$ ungefähr 5,8 %. Daraus folgt der Ausdruck ${\displaystyle {\frac {200h}{500-29h/r}}}$, der den Schwerpunkt im Bereich von ${\displaystyle (0\leq h\leq r)}$ mit einer Genauigkeit von besser als 5 Promille angibt. Die exakte Lage des Flächenschwerpunktes ${\displaystyle z_{s}(h)}$ im gesamten Bereich von ${\displaystyle (0<h\leq 2r)}$ findet man mittels Einsetzen von ${\displaystyle \alpha =\arccos(1-h/r)}$ in die Formel für den auf den Kreismittelpunkt bezogenen Schwerpunkt^[15] ${\displaystyle 4r\sin(\alpha )^{3}/(6\alpha -3\sin(2\alpha ))}$ :

${\displaystyle z_{s}=h-r+{\frac {2\left({\sqrt {h(2r-h)}}\right)^{3}}{3\left((h-r){\sqrt {h(2r-h)}}+r^{2}\arccos(1-h/r)\right)}}}$.

War zu Beginn eine Verschiebung oder Drehung notwendig, so muss der Schwerpunkt wieder entsprechend zurückverschoben werden.

Körper

Für dreidimensionale Körper kann man sowohl den Volumenschwerpunkt, also den Schwerpunkt des Vollkörpers, als auch den Flächenschwerpunkt, also den Schwerpunkt der Fläche, die den Körper begrenzt, berechnen.

Pyramide und Kegel

Um den Volumenschwerpunkt und den Flächenschwerpunkt einer Pyramide oder eines Kegels zu berechnen, verschiebt man sie im schiefwinkligen Koordinatensystem, so dass der Schwerpunkt der Grundfläche im Koordinatenursprung ${\displaystyle (0,0,0)}$ liegt, und die y-Achse durch die Spitze geht. Dann kann der Volumenschwerpunkt einer Pyramide oder eines Kegels durch^[16]

${\displaystyle x_{s}=0,\qquad y_{s}={\frac {h}{4}},\qquad z_{s}=0}$

und der Flächenschwerpunkt der Mantelfläche durch

${\displaystyle x_{s}=0,\qquad y_{s}={\frac {h}{3}},\qquad z_{s}=0}$

berechnet werden.

Rotationsparaboloid

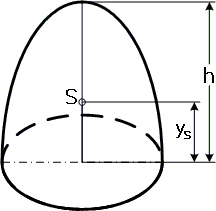
Um den Volumenschwerpunkt und den Flächenschwerpunkt eines Rotationsparaboloids zu berechnen, wird es im kartesischen Koordinatensystem verschoben, so dass der Schwerpunkt der Grundfläche im Koordinatenursprung ${\displaystyle (0,0,0)}$ liegt. Dann kann man den Volumenschwerpunkt des Rotationsparaboloids durch

${\displaystyle x_{s}=0,\qquad y_{s}={\frac {h}{3}},\qquad z_{s}=0}$

berechnen. Der Flächenschwerpunkt sieht ein wenig komplizierter aus. Für die Komponenten ${\displaystyle x_{s}}$ und ${\displaystyle z_{s}}$ gilt ebenfalls wieder

${\displaystyle x_{s}=z_{s}=0}$

und die Komponente ${\displaystyle y_{s}}$ liegt bei

${\displaystyle y_{s}=h-{\frac {4\pi {\sqrt {f}}\int _{0}^{h}y{\sqrt {f+y}}\,\mathrm {d} y}{4\pi {\sqrt {f}}\int _{0}^{h}{\sqrt {f+y}}\,\mathrm {d} y}}=h\left(1+{\frac {2}{5}}(f/h)-{\frac {3/5}{1-1/(1+h/f)^{3/2}}}\right),}$

wobei der Ausdruck im Nenner des ersten Bruchs die Mantelfläche der nach rechts geöffneten Parabel ${\displaystyle y=2{\sqrt {fx}}}$ mit der Brennweite f darstellt. Ab ${\displaystyle (f/h)\gtrsim 3}$ strebt ${\displaystyle y_{s}}$ gegen ${\displaystyle {\tfrac {1}{2}}h}$, anderenfalls gegen ${\displaystyle {\tfrac {2}{5}}h}$.

Kugelsegment

Um den Volumenschwerpunkt und den Flächenschwerpunkt eines Kugelsegments zu berechnen, verschiebt man das Segment im kartesischen Koordinatensystem, so dass der Mittelpunkt der Vollkugel im Koordinatenursprung ${\displaystyle (0,0,0)}$ liegt. Der Volumenschwerpunkt wird dann durch^[17]

${\displaystyle x_{s}=0,\quad y_{s}={\frac {3(2r-h)^{2}}{4(3r-h)}},\quad z_{s}=0}$

und der Flächenschwerpunkt durch

${\displaystyle x_{s}=0,\quad y_{s}=r-{\frac {h}{2}},\quad z_{s}=0}$

berechnet. (${\displaystyle 0\leq h\leq 2\,r}$)

Zusammenfassen von Schwerpunkten

Es ist möglich, mehrere Schwerpunkte einzelner Figuren zu einem gemeinsamen Schwerpunkt der Gesamtfigur zusammenzufassen, so dass sich der Schwerpunkt einer zusammengesetzten Figur aus den Schwerpunkten einzelner einfacher Elemente ergibt.

eindimensional	zweidimensional	dreidimensional	allgemein
${\displaystyle x_{s}={\frac {\sum \limits _{i}(x_{s,i}\cdot l_{i})}{\sum \limits _{i}l_{i}}}}$	${\displaystyle x_{s}={\frac {\sum \limits _{i}(x_{s,i}\cdot A_{i})}{\sum \limits _{i}A_{i}}}}$ ${\displaystyle y_{s}={\frac {\sum \limits _{i}(y_{s,i}\cdot A_{i})}{\sum \limits _{i}A_{i}}}}$	${\displaystyle x_{s}={\frac {\sum \limits _{i}(x_{s,i}\cdot V_{i})}{\sum \limits _{i}V_{i}}}}$ ${\displaystyle y_{s}={\frac {\sum \limits _{i}(y_{s,i}\cdot V_{i})}{\sum \limits _{i}V_{i}}}}$ ${\displaystyle z_{s}={\frac {\sum \limits _{i}(z_{s,i}\cdot V_{i})}{\sum \limits _{i}V_{i}}}}$	${\displaystyle {\vec {r}}_{s}={\frac {\sum \limits _{i}({\vec {r}}_{s,i}\cdot V_{i})}{\sum \limits _{i}V_{i}}}}$

Die Koordinaten ${\displaystyle x_{s}}$, ${\displaystyle y_{s}}$ und ${\displaystyle z_{s}}$ sind in einem frei wählbaren, aber einheitlichen kartesischen Koordinatensystem anzugeben. Weist eine Fläche (ein Körper) Aussparungen auf, so können obige Summenformeln ebenfalls angewendet werden unter Berücksichtigung, dass die ausgesparten Flächen (Volumen) mit negativem Vorzeichen in die Berechnung eingehen. Die Komponenten ${\displaystyle x_{s},\,y_{s},\,z_{s}}$ des Schwerpunkts bilden den Vektor ${\displaystyle {\vec {r}}_{s}}$.

Definition des Schwerpunkts durch Integrale

Die Formeln zur Berechnung des Schwerpunkts elementargeometrischer Figuren können mit den nachfolgend angegebenen Integralen hergeleitet werden. Bei komplizierteren Figuren lassen sich diese Integrale häufig nur numerisch bestimmen.

Die Definition entspricht mathematisch der Mittelung aller Punkte des geometrischen Objekts (Körpers) im euklidischen Raum ${\displaystyle \mathbb {R} ^{3}}$. Bei Linien und Flächen im zweidimensionalen Raum ${\displaystyle \mathbb {R} ^{2}}$ sind nur die Koordinaten ${\displaystyle x_{S}}$ und ${\displaystyle y_{S}}$ zu berechnen, die ${\displaystyle z}$-Koordinate entfällt. Der Integrationsbereich ist bei Linien eindimensional, bei Flächen zweidimensional und bei Körpern dreidimensional.

Linie

Für eine Linie ${\displaystyle C}$ der Länge ${\displaystyle L}$ ergibt sich der Schwerpunkt ${\displaystyle {\vec {r}}_{S}=(x_{S},y_{S},z_{S})}$ durch

${\displaystyle x_{S}={\frac {1}{L}}\int _{C}x\,\mathrm {d} s,\quad y_{S}={\frac {1}{L}}\int _{C}y\,\mathrm {d} s,\quad z_{S}={\frac {1}{L}}\int _{C}z\,\mathrm {d} s}$

mit

${\displaystyle \quad L=\int _{C}\,\mathrm {d} s.}$

Diese Integrale sind Wegintegrale erster Art.

Flächen

Für eine Fläche ${\displaystyle F}$ mit Flächeninhalt ${\displaystyle A}$ ist der Schwerpunkt definiert durch

${\displaystyle x_{S}={\frac {1}{A}}\int _{F}x\,\mathrm {d} A,\quad y_{S}={\frac {1}{A}}\int _{F}y\,\mathrm {d} A,\quad z_{S}={\frac {1}{A}}\int _{F}z\,\mathrm {d} A}$

mit

${\displaystyle \quad A=\int _{F}\mathrm {d} A.}$

Diese Integrale sind Oberflächenintegrale mit skalarem Flächenelement.

Körper

Im Fall eines beschränkten Körpers ${\displaystyle K}$ im dreidimensionalen Raum mit Volumen ${\displaystyle V}$ ist der Schwerpunkt definiert durch

${\displaystyle x_{S}={\frac {1}{V}}\int _{K}x\,\mathrm {d} V,\quad y_{S}={\frac {1}{V}}\int _{K}y\,\mathrm {d} V,\quad z_{S}={\frac {1}{V}}\int _{K}z\,\mathrm {d} V}$

mit

${\displaystyle \quad V=\int _{K}\mathrm {d} V.}$

Diese Integrale sind Volumenintegrale.

Allgemein

Sei ${\displaystyle K\subset \mathbb {R} ^{n}}$ ein Körper mit dem Volumen ${\displaystyle V}$. Der Schwerpunkt ${\displaystyle x_{S}=(x_{s,1},\ldots ,x_{s,n})\in \mathbb {R} ^{n}}$ von ${\displaystyle K}$ ist definiert durch

${\displaystyle x_{s,i}={\frac {1}{V}}\int _{K}x_{i}\,\mathrm {d} V\ \quad {\text{mit}}\quad V=\int _{K}\mathrm {d} V,}$

wobei ${\displaystyle \mathrm {d} V}$ das m-dimensionale Volumenelement und ${\displaystyle m}$ die Dimension von ${\displaystyle K}$, mit ${\displaystyle m\leq n}$ ist.^[18][19]

Integration bei symmetrischen Objekten

Bei Objekten, die Symmetrieelemente, z. B. eine Symmetrieachse oder eine Symmetrieebene besitzen, vereinfacht sich die Berechnung des Schwerpunkts in vielen Fällen, da der Schwerpunkt immer im Symmetrieelement enthalten ist. Hat das Objekt eine Symmetrieachse, so kann das Volumenelement in Abhängigkeit vom infinitesimalen Achsenelement ausgedrückt werden. Es braucht also nur noch über die Symmetrieachse integriert zu werden.^[20]

Alternative Integralformel für Flächen in der Ebene

Eine andere Möglichkeit, die Schwerpunktskoordinaten einer Fläche zu errechnen, ergibt sich durch die Formeln:

${\displaystyle x_{s}={\frac {\int _{a}^{b}(x(f(x)-g(x)))\,\mathrm {d} x}{\int _{a}^{b}(f(x)-g(x))\,\mathrm {d} x}}}$, ${\displaystyle y_{s}={\frac {\int _{a}^{b}(f(x)^{2}-g(x)^{2})\,\mathrm {d} x}{\int _{a}^{b}(2(f(x)-g(x)))\,\mathrm {d} x}},}$

wobei die Grenzen ${\displaystyle a}$ und ${\displaystyle b}$ die Schnittpunkte der Funktionen ${\displaystyle f(x)}$ und ${\displaystyle g(x)}$ darstellen. Durch diese Formel lässt sich der Schwerpunkt einer beliebigen ebenen Fläche, die zwischen zwei Funktionen eingeschlossen ist, berechnen. Bedingungen hierfür sind ${\displaystyle a<x<b}$, ${\displaystyle g(x)<y<f(x).}$^[21]

Beispiele zur Integralrechnung

Linienschwerpunkt eines Kreisbogens

Punkte auf einem ebenen Kreisbogen können am einfachsten in Polarkoordinaten angegeben werden. Wenn die y-Achse auf der Symmetrielinie mit Ursprung im Kreismittelpunkt liegt, lauten die Koordinaten:

${\displaystyle x=r\sin \varphi ,\,y=r\cos \varphi .}$

Die Länge ${\displaystyle b}$ des Kreisbogens ergibt sich zu:

${\displaystyle b=\int _{K}\mathrm {d} s=\int _{-\alpha }^{\alpha }r\mathrm {d} \varphi =2r\alpha ,}$

wobei das infinitesimale Längenelement ${\displaystyle \mathrm {d} s}$ durch ${\displaystyle r\mathrm {d} \varphi }$ substituiert werden kann.

Aus Symmetriegründen ist ${\displaystyle x_{S}=0}$. Für die y-Koordinate des Linienschwerpunkts ergibt sich aus der Definitionsgleichung:

${\displaystyle y_{S}={\frac {1}{b}}\int _{K}y\,\mathrm {d} s={\frac {1}{b}}\int _{-\alpha }^{\alpha }r^{2}\cos \varphi \,\mathrm {d} \varphi .}$

Die Integration in den Grenzen ergibt dann

${\displaystyle y_{S}={\frac {r^{2}}{b}}2\sin \alpha =r{\frac {l}{b}}.}$

Flächenschwerpunkt einer Parabel

Zur praktischen Bestimmung der x-Koordinate des Schwerpunktes im zweidimensionalen Fall substituiert man ${\displaystyle \mathrm {d} A}$ mit ${\displaystyle y\cdot \mathrm {d} x}$, was einem infinitesimalen Flächenstreifen entspricht. Ferner entspricht hierbei ${\displaystyle y}$ der die Fläche begrenzenden Funktion ${\displaystyle y(x)}$.

Für die praktische Berechnung der y-Koordinate im zweidimensionalen Fall gibt es prinzipiell zwei Vorgehensweisen:

• Entweder man bildet Umkehrfunktion ${\displaystyle x(y)}$ und berechnet das Integral ${\displaystyle \textstyle \int _{A}y\,\mathrm {d} A=\int _{y}y\cdot x(y)\,\mathrm {d} y}$, wobei die „neuen“ Integrationsgrenzen nun auf der y-Achse zu finden sind,
• oder man nutzt aus, dass der Schwerpunkt eines jeden zur y-Achse parallelen infinitesimalen Flächenstreifen ${\displaystyle {\tfrac {y(x)}{2}}}$ ist. Dann erhält man zur Bestimmung der y-Koordinate eine einfachere Formel, mit deren Hilfe das Bilden der Umkehrfunktion erspart bleibt:

Wir suchen den Flächenschwerpunkt jener Fläche, die durch eine Parabel ${\displaystyle y=x^{2}-4}$ und durch die x-Achse definiert ist (siehe nebenstehende Abbildung).

Zuerst bestimmen wir den Inhalt ${\displaystyle A}$ der Fläche

${\displaystyle A=\left|\int \limits _{-2}^{2}(x^{2}-4)\,\mathrm {d} x\right|={\frac {32}{3}}}$

Die Grenzen des Integrals sind bei Begrenzung der Fläche durch die x-Achse die Nullstellen der Funktion.

Die ${\displaystyle x}$-Koordinate des Schwerpunktes ergibt sich zu

${\displaystyle x_{s}={\frac {1}{A}}\int \limits _{-2}^{2}\int \limits _{y(x)}^{0}x\,\mathrm {d} y\,\mathrm {d} x=-{\frac {1}{A}}\int \limits _{-2}^{2}x\cdot y(x)\,\mathrm {d} x=-{\frac {1}{A}}\int \limits _{-2}^{2}x\cdot (x^{2}-4)\,\mathrm {d} x=0.}$

Die ${\displaystyle y}$-Koordinate ergibt sich zu

${\displaystyle y_{s}={\frac {1}{A}}\int \limits _{-2}^{2}\int \limits _{y(x)}^{0}y\,\mathrm {d} y\,\mathrm {d} x=-{\frac {1}{2A}}\int \limits _{-2}^{2}[y(x)]^{2}\,\mathrm {d} x=-{\frac {1}{2A}}\int \limits _{-2}^{2}(x^{4}-8x^{2}+16)\,\mathrm {d} x=-1{,}6.}$

Siehe auch

• Satz von Commandino
• Seitenhalbierende

Literatur

• Hermann Athen, Jörn Bruhn (Hrsg.): Lexikon der Schulmathematik und angrenzender Gebiete. Band 4: S bis Z. Aulis Verlag, Köln 1978, ISBN 3-7614-0242-2, S. 943–944. 
• H. S. M. Coxeter: Unvergängliche Geometrie. Ins Deutsche übersetzt von J. J. Burckhardt (= Wissenschaft und Kultur. Band 17). Birkhäuser Verlag, Basel/Stuttgart 1963 (MR0692941). 
• Egbert Harzheim: Einführung in die Kombinatorische Topologie (= Die Mathematik. Einführungen in Gegenstand und Ergebnisse ihrer Teilgebiete und Nachbarwissenschaften). Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-07016-X (MR0533264). 
• Jens Levenhagen, Manfred Spata: Die Bestimmung von Flächenmittelpunkten. In: Vermessungswesen und Raumordnung Band 60, 1998, S. 31–42.
• Harald Scheid (Hrsg.): Duden: Rechnen und Mathematik. 4., völlig neu bearbeitete Auflage. Bibliographisches Institut, Mannheim / Wien / Zürich 1985, ISBN 3-411-02423-2. 
• Thomas Westermann: Mathematik für Ingenieure. Springer, 2011, ISBN 978-3-642-12759-5, S. 336–338 (Auszug in der Google-Buchsuche).

Weblinks

• Schwerpunkt von Figuren auf mathematische-basteleien.de
• Center of Mass auf Paul’s Online Math Notes – Calculus II, Lamar University
• Herleitung von Formeln zum Schwerpunkt beim Dreieck
• @1@2Vorlage:Toter Link/www.zum.deFlash-Animation zur Schwerpunkt-Konstruktion beim Dreieck (Seite nicht mehr abrufbar. Suche in Webarchiven) (dwu-Unterrichtsmaterialien)

Einzelnachweise

1. ↑ Denkmal zur Trennung Tirols vor 100 Jahren orf.at, 10. Oktober 2020, abgerufen 10. Oktober 2020. – Markstein Mitte Tirols (…). „Wird um die Grenzen des Historischen Tirols ein Rechteck gelegt und in diesem zwei Diagonalen gezogen, so befindet sich der Mittelpunkt des historischen Tirols in Latzfons …“.
2. ↑ Egbert Harzheim: Einführung in die Kombinatorische Topologie. 1978, S. 31 ff.
3. ↑ Hermann Athen, Jörn Bruhn (Hrsg.): Lexikon der Schulmathematik und angrenzender Gebiete. Band 4: S bis Z. 1978, S. 944
4. ↑ Coxeter, op. cit., S. 242
5. ↑ DUDEN: Rechnen und Mathematik. 1985, S. 652
6. ↑ Alfred Böge, Technische Mechanik. Vieweg + Teubner 2009, S. 84 (eingeschränkte Vorschau in der Google-Buchsuche)
7. ↑ Alfred Böge: Technische Mechanik. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1355-8, S. 77. 
8. ↑ Friedrich Joseph Pythagoras Riecke (Hrsg.): Mathematische Unterhaltungen. Erstes Heft. 1973, S. 76
9. ↑ Den Beweis von Riecke (und einen anderen Beweis) findet man im Beweisarchiv.
10. ↑ Calculating the area and centroid of a polygon (Memento vom 22. September 2009 im Internet Archive)
11. ↑ Lothar Papula: Mathematische Formelsammlung für Ingenieure und Naturwissenschaftler. Vieweg, Wiesbaden 2006, ISBN 978-3-8348-0156-2, S. 32–38. 
12. ↑ Hans Walser: 2. Im Dreieck. (PDF) Schwerpunkt. Mathematikinformation, S. 4, abgerufen am 18. Oktober 2022. 
13. ↑ R. Lauenstein: 2) Das Viereck. (PDF) Die Graphische Statik. Universität Krakau, S. 28, abgerufen am 18. Oktober 2022. 
14. ↑ Frank Jablonski: Schwerpunkt (Memento vom 11. Dezember 2009 im Internet Archive), Universität Bremen, S. 114 (PDF; 688 kB)
15. ↑ Alfred Böge et al.: Handbuch Maschinenbau: Grundlagen und Anwendungen der Maschinenbau-Technik. Springer 2013, Seite C14, Gl. (39)
16. ↑ S. 34
17. ↑ S. 38
18. ↑ Centroid. In: M. Hazewinkel: Encyclopedia of Mathematics. („center of a compact set“)
19. ↑ Norbert Henze, Günter Last: Mathematik für Wirtschaftsingenieure und für naturwissenschaftlich-technische Studiengänge – Band II. Vieweg+Teubner, 2004, ISBN 3-528-03191-3, S. 128 (Auszug in der Google-Buchsuche)
20. ↑ David Halliday, Robert Resnick, Jearl Walker: Halliday Physik für natur- und ingenieurwissenschaftliche Studiengänge. 3. Auflage. Wiley-VCH-Verlag, Weinheim 2020, ISBN 978-3-527-41368-3, S. 116 (eingeschränkte Vorschau in der Google-Buchsuche). 
21. ↑ Thomas Westermann: Mathematik für Ingenieure. Springer 2015, ISBN 978-3-642-54290-9, S. 338.