Satz des Euklid

Der Satz des Euklid, manchmal auch Satz von Euklid, ist ein Lehrsatz aus der elementaren Zahlentheorie und besagt, dass es unendlich viele Primzahlen gibt. Benannt ist er nach Euklid von Alexandria, der ihn als Erster im dritten Jahrhundert v. Chr. in seinen Elementen bewies. Jedoch kannten die Mathematiker der Antike das Konzept der Unendlichkeit noch nicht. Euklid selbst formulierte den Satz daher wie folgt: „Es gibt mehr Primzahlen als jede vorgelegte Anzahl von Primzahlen.“

Eine Primzahl ist eine ganze Zahl größer als 1, die nur durch 1 und sich selbst ohne Rest teilbar ist. Die ersten Primzahlen sind 2, 3, 5 und 7. Der Satz des Euklid besagt, dass die Liste 2, 3, 5, 7, 11, 13, 17… aller Primzahlen nicht endet, genauso wie die Liste 1, 2, 3, 4, 5, 6 … aller natürlichen Zahlen nicht endet.

Der ursprüngliche von Euklid geführte Beweis ist direkt und konstruktiv. Zu einer gegebenen endlichen Liste von Primzahlen wird stets eine weitere noch nicht vorhandene Primzahl erzeugt, ohne diese jedoch explizit anzugeben. Vielmehr wird argumentiert, dass jede endliche Liste von Primzahlen unvollständig ist. Daraus wird gefolgert, dass es unendlich viele Primzahlen gibt. In der späteren Literatur wird oft fälschlicherweise behauptet, dass Euklids Argument anhand eines Widerspruchsbeweises aufgeführt sei. Jedoch lässt sich der Beweis leicht zu einem Widerspruchsbeweis umformulieren.

Nach dem Fundamentalsatz der Arithmetik können alle natürlichen Zahlen größer als 1 eindeutig in Primfaktoren zerlegt werden. Der Satz des Euklid ist daher eines der grundlegendsten Resultate der Zahlentheorie, da er zeigt, dass es unendlich viele unzerlegbare Grundbausteine der Zahlen gibt. Im Laufe der Zeit wurden neben Euklids Originalbeweis zahlreiche andere Beweise gefunden, die teilweise mathematische Techniken aus der Analysis, Kombinatorik oder auch der Topologie nutzen. Ab dem 19. Jahrhundert konnten zudem mit den Beweisen des Dirichletschen Primzahlsatzes und des Primzahlsatzes weitreichende Verallgemeinerungen erzielt werden. Während der Satz des Euklid lediglich aussagt, dass die Anzahl der Primzahlen unendlich groß ist, formulieren die modernen Primzahlsätze Regeln, wie häufig Primzahlen in gewissen Bereichen ungefähr anzutreffen sind.

Analoge Fragestellungen hinsichtlich der Häufigkeit von Primzahlzwillingen, Mersenne-Primzahlen oder Fermat-Primzahlen verbleiben bis heute unbeantwortet.

Beweis von Euklid

Der Satz wurde erstmals^[1] in Euklids Elementen im neunten Buch, Proposition 20, niedergeschrieben.

Originalformulierung

Euklids Ausführung kann wie folgt ins Deutsche übersetzt werden:

• 
  Die geometrische Anschauung des Beweises von Euklid. Abgebildet sind die Strecken ${\displaystyle a=2,}$ ${\displaystyle b=3}$ und ${\displaystyle c=5,}$ die allesamt als ganzes Vielfaches in die Strecke ${\displaystyle DE}$ mit ${\displaystyle a\cdot b\cdot c=30}$ Längeneinheiten passen. Wird nun dieser Strecke ${\displaystyle DE}$ jedoch noch eine weitere Einheit ${\displaystyle DF=1}$ zugefügt, so kann die resultierende Strecke ${\displaystyle EF}$ weder von ${\displaystyle a}$ noch von ${\displaystyle b}$ noch von ${\displaystyle c}$ „gemessen“ werden.

Erläuterungen: Zu jeder endlichen Menge von Primzahlen (gegebenes Objekt) gibt es danach eine Primzahl (gesuchtes Objekt), die dieser Menge nicht angehört. Euklid beweist dies konstruktiv, indem er ein Verfahren beschreibt, aus gegebenen endlich vielen Primzahlen ${\displaystyle p_{1},\dotsc ,p_{n}}$ (Euklid behandelt hier den Fall ${\displaystyle n=3}$) eine neue Primzahl zu gewinnen, indem man die Zahl ${\displaystyle p_{1}\cdot p_{2}\dotsm p_{n}+1}$ bildet und einen ihrer Primfaktoren bestimmt. Im Beweis wird geometrisch-anschaulich argumentiert, indem gesagt wird, dass eine Strecke (Zahl) eine andere „misst“, wenn letztere durch erstere teilbar ist. In Euklids Ausführungen geht ferner sein bereits in Buch VII, Proposition 31 (die lautet: Jede zusammengesetzte Zahl wird von irgendeiner Primzahl gemessen)^[5] beschriebenes Verfahren zur effektiven Gewinnung eines Primfaktors einer vorgegebenen Zahl als „Unterprogramm“ ein.^[6] Da Euklid im Originalwerk keine Möglichkeit hatte, eine willkürliche Liste von Primzahlen zu schreiben, verwendete er eine Methode, die er häufig anwandte, nämlich die Methode des verallgemeinerbaren Beispiels. Dabei wählt er nur drei Primzahlen aus und beweist mit der oben skizzierten allgemeinen Methode, dass er immer eine zusätzliche Primzahl finden kann. Euklid ging vermutlich davon aus, dass seine Leser davon überzeugt wären, dass ein ähnlicher Beweis funktionieren wird, egal wie viele Primzahlen ursprünglich ausgewählt werden.^[7]

Veranschaulichung des Beweises an einem Beispiel

Die Beweisidee von Euklid lässt sich über folgendes Beispiel veranschaulichen. Dieses verwendet die ersten drei Primzahlen 2, 3 und 5. Aus diesen kann mit Euklids Methode eine neue Primzahl konstruiert werden, die in der Liste noch nicht vorkommt. Dafür wird die Zahl

${\displaystyle 2\cdot 3\cdot 5+1=31}$

betrachtet, die aus dem Produkt der Listenzahlen mit anschließender Addition von 1 gebildet wird. Diese Zahl 31 ist nun weder durch 2 noch durch 3 noch durch 5 teilbar. Das folgt daraus, dass die Differenz zweier Zahlen mit gemeinsamem Teiler wieder diesen Teiler hat: Es ist ${\displaystyle 30=2\cdot 3\cdot 5}$ nach Konstruktion durch 2, 3 und 5 teilbar – hätte auch ihr Nachfolger 31 diese Eigenschaft, so auch ${\displaystyle 31-30=1.}$ Doch die 1 wird nur von 1 selbst geteilt. In der Tat ist 31 zum Beispiel wieder eine (neue) Primzahl und ungleich 2, 3 und 5.

In heutiger Fachsprache

Trotz Euklids direkter Argumentation wird der Satz des Euklid von vielen Autoren in Standardwerken der Zahlentheorie als ein Widerspruchsbeweis wiedergegeben, zum Beispiel bei Jörg Brüdern oder Tom M. Apostol.^[8][9]

In der Sprechweise der heutigen Mengenlehre stellt Euklid die folgende Behauptung auf:

Gegeben sei eine endliche Menge ${\displaystyle M=\{p_{1},p_{2},\dotsc ,p_{n}\}}$ von paarweise verschiedenen Primzahlen ${\displaystyle p_{1},\dotsc ,p_{n}.}$ Dann gibt es mindestens eine weitere Primzahl ${\displaystyle p_{n+1},}$ die nicht in ${\displaystyle M}$ enthalten ist.

Dazu bildet Euklid das kleinste Vielfache ${\displaystyle m=p_{1}\cdot p_{2}\dotsm p_{n}}$ aller Primzahlen aus ${\displaystyle M.}$ Dabei ist wichtig, dass alle bisherigen Primzahlen Teiler von ${\displaystyle m}$ sind. Dann bildet er ${\displaystyle m+1}$ und unterscheidet zwei Fälle:

1. ${\displaystyle m+1=:p_{n+1}}$ ist Primzahl, dann ist ${\displaystyle p_{n+1}\not \in M}$ eine weitere Primzahl.
2. ${\displaystyle m+1}$ ist keine Primzahl, dann hat ${\displaystyle m+1}$ einen Primteiler ${\displaystyle q.}$ Angenommen, es wäre ${\displaystyle q=:p_{i}\in M,}$ dann wäre ${\displaystyle q}$ ein Teiler von ${\displaystyle m.}$ Es ist aber auch Teiler von ${\displaystyle m+1}$ und müsste folglich auch Teiler der Differenz ${\displaystyle (m+1)-m=1}$ sein. Ein Widerspruch!

Der Beweis kommt auch ohne die Fallunterscheidung aus:^[8]

Angenommen, es gäbe nur endlich viele Primzahlen, etwa ${\displaystyle p_{1},\dotsc ,p_{r}.}$ Dann wäre die Zahl ${\displaystyle p_{1}p_{2}\dotsm p_{r}+1}$ wegen des Fundamentalsatzes der Arithmetik durch ein ${\displaystyle p_{j}}$ teilbar, also auch ${\displaystyle p_{j}|1,}$ ein Widerspruch.

Beurteilung des Beweises

Von Euklid wird oft fälschlicherweise berichtet, er habe sein Ergebnis durch Widerspruch bewiesen, beginnend mit der Annahme, dass die ursprünglich betrachtete endliche Menge alle Primzahlen enthält,^[10] obwohl es sich eigentlich um einen Beweis durch Fallunterscheidung, also eine direkte Beweismethode handelt. Der Philosoph Torkel Franzén stellte fest: „Euklids Beweis, dass es unendlich viele Primzahlen gibt, ist kein indirekter Beweis […]. Das Argument wird manchmal als indirekter Beweis formuliert, indem man es durch die Annahme ersetzt: ‚Angenommen ${\displaystyle q_{1},\dotsc ,q_{n}}$ sind alle Primzahlen.‘ Da diese Annahme jedoch nicht einmal im Beweis verwendet wird, ist die Neuformulierung sinnlos.“^[11]

Benno Artmann sieht im Beweis von Euklid ein Beispiel der Verwendung „endlicher Mittel zur Beherrschung des Unendlichen“. In dieser Hinsicht habe Euklid „Bahnbrechendes“ geleistet. Jedoch bildeten die Primzahlen nur ein Beispiel dieses Prinzips in Euklids Schaffen. Im selben Kontext wird seine Theorie der Parallelen und Kreistangenten sowie „Unvereinbarkeit“ (im Sinne des Euklidischen Algorithmus) von Artmann genannt.^[12]

Die Zahlentheoretiker Gérald Tenenbaum und Michel Mendès France nennen Euklids Argument „wundervoll in seiner Schönheit und Einfachheit“ und weisen darauf hin, dass es sich in moderner Fachsprache auf die vier Symbole

${\displaystyle n!+1}$

reduzieren lässt. Dabei ist ${\displaystyle !}$ die Fakultät von ${\displaystyle n}$ und die erzeugte Zahl ist durch keine Zahl zwischen ${\displaystyle 2\leq k\leq n}$ teilbar, weshalb es Primzahlen geben muss, die größer als ${\displaystyle n}$ sind.^[13]

Der Beweis von Euklid wird, hinsichtlich der fundamentalen Bedeutung des Resultats für die Zahlentheorie, wegen seiner Einfachheit bis heute als elegant erachtet.^[8] Dennoch liefert er keine starke Methode, zu schätzen, wie viele Primzahlen es unter einer Schranke ${\displaystyle x}$ mindestens gibt. Zwar kann die Schranke ${\displaystyle \pi (x)>\log(\log(x))}$, mit der Primzahlen abzählenden Funktion ${\displaystyle \pi }$, induktiv aus Euklids Methode abgeleitet werden, doch dieses Resultat wird für die analytische Zahlentheorie als unbrauchbar angesehen.^[8] Dabei ist ${\displaystyle \log(x)}$ der natürliche Logarithmus von ${\displaystyle x}$. Bereits mit nicht wesentlich schwierigeren Argumenten, zum Beispiel durch Ideen von Leonhard Euler und Pafnuti Lwowitsch Tschebyschow, können wesentlich stärkere Schranken für die Primzahlverteilung hergeleitet werden.^[14] Dazu zählt die Schranke

${\displaystyle c_{2}{\frac {x}{\log(x)}}<\pi (x)<c_{1}{\frac {x}{\log(x)}}}$

für existierende Konstanten ${\displaystyle c_{1}>c_{2}>0}$ für alle ${\displaystyle x>2}$.^[15]

Bedeutung

Erzeugung neuer Primzahlen

Der Beweis des Satzes des Euklid zeigt eine Möglichkeit auf, wie aus einer oder mehreren vorgegebenen Primzahlen ${\displaystyle p_{1},p_{2},\dotsc ,p_{k}}$ mindestens eine weitere Primzahl berechnet werden kann. Dazu bildet man das Produkt dieser Zahlen und addiert 1 zu dem Produkt, also

${\displaystyle n:=p_{1}p_{2}\dotsm p_{k}+1=\prod _{i=1}^{k}p_{i}+1.}$

Das Symbol ${\displaystyle \textstyle \prod }$ ist das Produktzeichen. Wegen ${\displaystyle n>1}$ gibt es einen kleinsten Teiler ${\displaystyle d>1}$ von ${\displaystyle n}$. Dieser ist notwendigerweise eine Primzahl und teilerfremd zu ${\displaystyle p_{1},\dotsc ,p_{k}}$. Daher ist mit ${\displaystyle d}$ eine neue Primzahl gefunden.

Zieht man nur die Mengen der ersten aufeinanderfolgenden Primzahlen in Betracht, also ${\displaystyle p_{1}=2,p_{2}=3,p_{3}=5,\dotsc }$, und bildet daraus die Zahlen

${\displaystyle P_{r}:=2\cdot 3\dotsm p_{r}+1=\prod _{i=1}^{r}p_{i}+1,}$

dann stellen sich die ersten fünf dieser Zahlen als prim heraus, die nächsten fünf als zusammengesetzt. Beispielsweise ist

${\displaystyle P_{6}=2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13+1=30031=59\cdot 509.}$

Ist das Ergebnis von ${\displaystyle 2\cdot 3\dotsm p_{n}+1=p_{n}\#+1,}$ wobei das Symbol ${\displaystyle \#}$ für das Primorial von ${\displaystyle p_{n}}$ steht, wieder eine Primzahl, so nennt man diese auch Euklidische Primzahl. Ein etwas verallgemeinerter Begriff ist die Primorial-Primzahl, die durch ${\displaystyle p_{n}\#\pm 1}$ erzeugt wird. Es ist eine offene Frage, ob es unendlich viele Primorial-Primzahlen gibt. Die bis heute größte gefundene Primorial-Primzahl ist die ${\displaystyle 476\,311}$-stellige Zahl ${\displaystyle 1\,098\,133\#-1}$.^[16] Zum Überprüfen, ob eine Zahl prim ist, gibt es Primzahltests, wie den von Miller-Rabin. Die bis heute größte gefundene Primzahl ist jedoch die ${\displaystyle 24\,862\,048}$-stellige Mersenne-Primzahl ${\displaystyle 2^{82\,589\,933}-1}$.^[17]

Zahlentheoretische Forschung

Die Aussage, dass es unendlich viele Primzahlen gibt, führte zu der Frage, wie dicht sie in den natürlichen Zahlen liegen. Damit ist das langfristige Verhalten der Abstände zwischen verschiedenen Primzahlen gemeint. Zum Beispiel finden sich bis zur Zahl 10000 nur einhundert Quadratzahlen, also viel weniger als natürliche Zahlen. Analog dazu kann gefragt werden, wie häufig Primzahlen bis zu einer Schranke (wie zum Beispiel 10000) auftauchen und wie sich diese Häufigkeit verhält, wenn die Schranke immer größer gewählt wird.

Eine Folgerung des Beweises von Euklid für die Folge der Primzahlen ist die Ungleichung

${\displaystyle p_{n+1}<p_{1}\cdot p_{2}\dotsm p_{n}.}$

Diese konnte von Bonse weiter verbessert werden zu

${\displaystyle p_{n+1}^{2}<p_{1}\cdot p_{2}\dotsm p_{n}}$

für alle ${\displaystyle n\geq 4,}$ was auch Bonsesche Ungleichung genannt wird. Im Jahr 2000 bewies Michael Dalezman das etwas stärkere Resultat

${\displaystyle p_{n+1}p_{n+2}<p_{1}\cdot p_{2}\dotsm p_{n},}$

ebenfalls gültig für alle ${\displaystyle n\geq 4.}$^[18]

Durch den Satz des Euklid ist es ausgeschlossen, alle Primzahlen niederzuschreiben. Jedoch gibt es Bemühungen, im Detail zu schätzen, wie viele Primzahlen in gewissen Bereichen anzutreffen sind, zum Beispiel im Intervall ${\displaystyle [10^{12},10^{13}].}$ Approximative Antworten auf solche Fragen liefert der (weiter unten diskutierte) Primzahlsatz. Dieser konnte erst Ende des 19. Jahrhunderts streng bewiesen werden. Aber bereits 1859 hatte Bernhard Riemann eine Formel hergeleitet, welche die Verteilung der Primzahlen bis ins letzte Detail ausdrückt. Diese beinhaltet als entscheidende Zutat die Nullstellen der Riemannschen Zeta-Funktion, die definiert werden kann durch

${\displaystyle \zeta (s)=\prod _{p\,{\text{Primzahl}}}{\frac {1}{1-{\frac {1}{p^{s}}}}}={\frac {1}{\left(1-{\frac {1}{2^{s}}}\right)\left(1-{\frac {1}{3^{s}}}\right)\left(1-{\frac {1}{5^{s}}}\right)\left(1-{\frac {1}{7^{s}}}\right)\cdots }}.}$

Eine detailliertere Übersicht zu Verallgemeinerungen des Satzes des Euklid ist im Abschnitt Stärkere Resultate gegeben.

Für die Kryptographie

Große Primzahlen werden bei der Verschlüsselung von Daten (zum Beispiel im Internet) verwendet. Die Sicherheit solcher Systeme beruht auf der Annahme, dass es kein schnelles Verfahren gibt, eine Zahl in ihre Primfaktoren zu zerlegen. Beim RSA-Kryptosystem nimmt eine Person, die eine Nachricht verschlüsseln möchte, zwei große Primzahlen ${\displaystyle p}$ und ${\displaystyle q}$ mit großem Abstand zueinander, und bildet die zusammengesetzte Zahl ${\displaystyle pq=N.}$ Mit deren Hilfe können nun Nachrichten (wenn zuvor in Zahlen umgewandelt) durch einen öffentlichen Schlüssel, der aus ${\displaystyle p}$ und ${\displaystyle q}$ erzeugt wurde, verschlüsselt werden. Dieser Schlüssel steht jedermann zur Verfügung, gibt jedoch keine Einsicht in das Kryptosystem an sich. Mit dem Wissen um ${\displaystyle p}$ und ${\displaystyle q}$ kann eine Nachricht aus der Öffentlichkeit an den Privatmenschen anschließend wieder entschlüsselt werden, da mit dem Wissen um ${\displaystyle p}$ und ${\displaystyle q}$ auch der „Gegenschlüssel“ erzeugt werden kann, der den Klartext wieder herstellt. Dieser Gegenschlüssel steht nur der Privatperson zur Verfügung und ist daher ein privater Schlüssel. Zum Brechen des Systems ist folglich die Faktorisierung von ${\displaystyle N}$ erforderlich.

Der Satz des Euklid gewährleistet, dass beliebig große Primzahlen zur Erzeugung eines solchen Kryptosystems gefunden werden können.

Auswahl weiterer Beweise

Für den Satz des Euklid wurden seit dem achtzehnten Jahrhundert zahlreiche alternative Beweise gefunden, z. B. durch Christian Goldbach (1730), Leonhard Euler (1736, 1737), Victor-Amédée Lebesgue (1843,^[19] 1856,^[20] 1859,^[21] 1862^[22]), James Joseph Sylvester (1871,^[23] 1888^[24]), Leopold Kronecker (1875/76),^[25] Ernst Eduard Kummer (1878)^[26] sowie Thomas Jean Stieltjes (1890). Modernere Beweise stammen u. a. von George Pólya (1921),^[27] Paul Erdös (1934, 1938), Richard Bellman (1947),^[28] Hillel Fürstenberg (1955), André Weil (1979),^[29] Lawrence C. Washington (1980) und Andrew Granville (2007,^[30] 2009^[31]).^[32]

In diesem Artikel wird nur eine Auswahl an Beweisen aufgeführt.

Über die Fermat-Zahlen

Dieser Beweis geht auf Christian Goldbach aus dem Jahr 1730 zurück. Er entstammt einem Brief von Goldbach an Leonhard Euler vom 20. Juli.^[33] Über die Fermat-Zahlen lässt sich eine unendlich lange (monoton wachsende) Folge von natürlichen Zahlen konstruieren, die paarweise teilerfremd sind. Das heißt: Wenn man je zwei beliebige unterschiedliche Zahlen dieser Folge auswählt, haben diese keinen gemeinsamen Teiler. Da sie aber alle in Primfaktoren zerfallen, folgt schon der Satz des Euklid.

Es sei ${\displaystyle F_{n}=2^{2^{n}}+1}$ die ${\displaystyle n}$-te Fermat-Zahl. Die Teilerfremdheit von ${\displaystyle F_{a}}$ und ${\displaystyle F_{b}}$ für unterschiedliche ${\displaystyle a,b}$ wird über die Rekursionsformel

${\displaystyle \prod _{k=0}^{n-1}F_{k}=F_{n}-2}$

ersichtlich, die mittels vollständiger Induktion gezeigt werden kann.^[34] Gilt nun ${\displaystyle a<b}$ und ist ${\displaystyle d>0}$ ein gemeinsamer Teiler von ${\displaystyle F_{a}}$ und ${\displaystyle F_{b}}$, dann muss dieser wegen der obigen Formel (mit ${\displaystyle n=b}$) auch 2 teilen. Da die Fermat-Zahlen ungerade sind, ist schon ${\displaystyle d=1}$.^[35]

Beweis von Stieltjes

Im Jahr 1890 lieferte Thomas Jean Stieltjes den folgenden Beweis: Zu jeder endlichen Liste von paarweise verschiedenen Primzahlen ${\displaystyle p_{1},\dotsc ,p_{k}}$ wird das Produkt ${\displaystyle P=p_{1}\dotsm p_{k}}$ betrachtet. Ist ${\displaystyle p_{i}}$ eine dieser Primzahlen und ${\displaystyle P=AB}$ eine Zerlegung in ganze Zahlen ${\displaystyle A}$ und ${\displaystyle B}$, so kann ${\displaystyle p_{i}}$ nicht ${\displaystyle A}$ und ${\displaystyle B}$ teilen, da sonst ${\displaystyle p_{i}^{2}}$ bereits ${\displaystyle P}$ teilen würde, was dem Fundamentalsatz der Arithmetik widerspräche. Damit teilt keines der ${\displaystyle p_{i}}$ die Zahl ${\displaystyle A+B>1}$, weshalb es mehr als die Primzahlen der Liste geben muss.^[36]

Über die Transzendenz der Kreiszahl

Dieser Beweis wird J. Hacks im Jahr 1899 zugeschrieben.^[37] Dass die Kreiszahl ${\displaystyle \pi =3{,}141\dots }$ irrational ist, also nicht als Verhältnis zweier ganzer Zahlen geschrieben werden kann, konnte bereits von Johann Heinrich Lambert bewiesen werden.^[38] Im Jahr 1882 konnte Ferdinand von Lindemann dieses Resultat durch den Satz von Lindemann-Weierstraß verschärfen, indem er zeigte, dass ${\displaystyle \pi }$ sogar eine transzendente Zahl ist, d. h. niemals Nullstelle eines nicht-trivialen Polynoms mit ausschließlich rationalen Koeffizienten ist. Auf Leonhard Euler geht wiederum die Formel

${\displaystyle \prod _{p\,\mathrm {Primzahl} }{\frac {1}{1-{\frac {1}{p^{2}}}}}=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=1+{\frac {1}{4}}+{\frac {1}{9}}+{\frac {1}{16}}+{\frac {1}{25}}+\dotsb ={\frac {\pi ^{2}}{6}}}$

zurück. Diese Formel entsteht aus dem Euler-Produkt der Riemannschen Zeta-Funktion, ausgewertet an der Stelle ${\displaystyle s=2}$, und folgt aus der Tatsache, dass natürliche Zahlen eindeutig in Primfaktoren zerfallen. Dass das Ergebnis den Wert ${\displaystyle {\tfrac {\pi ^{2}}{6}}}$ annimmt, war lange nicht klar und Gegenstand des Basler Problems. Das Produkt auf der linken Seite durchläuft alle Primzahlen, man hat also

${\displaystyle {\frac {1}{1-{\frac {1}{4}}}}\cdot {\frac {1}{1-{\frac {1}{9}}}}\cdot {\frac {1}{1-{\frac {1}{25}}}}\cdot {\frac {1}{1-{\frac {1}{49}}}}\cdot {\frac {1}{1-{\frac {1}{121}}}}\dotsm ={\frac {4}{3}}\cdot {\frac {9}{8}}\cdot {\frac {25}{24}}\cdot {\frac {49}{48}}\cdot {\frac {121}{120}}\dotsm ={\frac {\pi ^{2}}{6}}.}$

Gäbe es nur endlich viele Primzahlen, dann wäre die linke Seite als Produkt endlich vieler rationaler Zahlen eine rationale Zahl. Die rechte Seite ${\displaystyle {\tfrac {\pi ^{2}}{6}}}$ ist jedoch, da ${\displaystyle \pi }$ als transzendente Zahl niemals Quadratwurzel einer rationalen Zahl ist, irrational.^[39] Dies erzeugt einen Widerspruch.

Ähnlich kann auch mit allen positiven geraden Zahlen argumentiert werden, da stets

${\displaystyle \prod _{p\,\mathrm {Primzahl} }{\frac {1}{1-{\frac {1}{p^{2k}}}}}\in \mathbb {Q} \pi ^{2k}\setminus \{0\}.}$

Dabei ist

${\displaystyle \mathbb {Q} \pi ^{2k}=\{r\cdot \pi ^{2k}\mid r\in \mathbb {Q} \}}$

die Menge aller rationalen Vielfachen von ${\displaystyle \pi ^{2k}}$. Seit dem Beweis der Irrationalität der Apéry-Konstante ${\displaystyle \zeta (3)}$ im Jahr 1979 ist diese Methode auch auf

${\displaystyle \prod _{p\,\mathrm {Primzahl} }{\frac {1}{1-{\frac {1}{p^{3}}}}}=\zeta (3)}$

anwendbar.^[40] Jedoch verwendet der Originalbeweis der Irrationalität von ${\displaystyle \zeta (3)}$, erbracht von Roger Apéry, den Primzahlsatz.

Über die Irrationalität der Eulerschen Zahl

Der Beweis der Irrationalität der Eulerschen Zahl ${\displaystyle e=2{,}71828\dots }$ konnte bereits 1737 von Leonhard Euler erbracht werden. Um mit dieser die Unendlichkeit der Primzahlen zu zeigen, wird die Möbiusfunktion ${\displaystyle \mu }$ benötigt,

${\displaystyle \mu (n)={\begin{cases}(-1)^{k},&{\mbox{wenn }}n{\mbox{ quadratfrei, wobei }}k{\mbox{ die Anzahl der Primfaktoren von }}n{\mbox{ ist}},\\0&{\mbox{sonst,}}\end{cases}}}$

die also u. a. stets den Wert 0 annimmt, falls die Eingabe ${\displaystyle n}$ durch eine Quadratzahl größer als 1 teilbar ist. Wie R. C. Buck im Jahre 1944 zeigen konnte, gilt für Werte ${\displaystyle x}$ mit ${\displaystyle |x|<1}$ die Identität^[41]

${\displaystyle \prod _{n=1}^{\infty }(1-x^{n})^{\frac {\mu (n)}{n}}=(1-x)\cdot {\frac {1}{\sqrt {1-x^{2}}}}\cdot {\frac {1}{\sqrt[{3}]{1-x^{3}}}}\cdot {\frac {1}{\sqrt[{5}]{1-x^{5}}}}\cdot {\sqrt[{6}]{1-x^{6}}}\dotsm =e^{-x}.}$

Gäbe es nur endlich viele Primzahlen ${\displaystyle p_{1},\dotsc ,p_{k},}$ so müsste jede Zahl ${\displaystyle n}$ größer als ${\displaystyle P=p_{1}\cdot p_{2}\dotsm p_{k}}$ durch eine Quadratzahl teilbar sein. Dies hat den Hintergrund, dass dann mindestens eine Primzahl doppelt in der Faktorisierung von ${\displaystyle n}$ vorkommen muss. Mit ${\displaystyle x=-{\tfrac {1}{P!}}}$ gälte dann:

${\displaystyle \prod _{n=1}^{P}\left(1-\left(-{\frac {1}{P!}}\right)^{n}\right)^{\mu (n){\frac {P!}{n}}}=e}$

Die linke Seite ist ein endliches Produkt rationaler Zahlen, doch die rechte Seite ist eine irrationale Zahl.^[40] Dies erzeugt einen Widerspruch.

Fürstenbergs topologischer Beweis

Im Jahr 1955 veröffentlichte Hillel Fürstenberg, damals noch Student an der Yeshiva University, einen Beweis des Satzes des Euklid, der lediglich topologische Mittel verwendet.^[42] Dabei werden, grob gesagt, bloß Eigenschaften von Mengensystemen ausgenutzt und ein Widerspruch erzeugt. Der Beweis überraschte die Mathematikergemeinschaft wegen seiner außergewöhnlichen Methodik. Der Kerngedanke von Fürstenberg ist, dass bei nur endlich vielen existierenden Primzahlen eine unmögliche Topologie konstruiert werden könnte.

Beim Beweis wird eine Topologie auf der Menge ${\displaystyle \mathbb {Z} }$ der ganzen Zahlen definiert. Dabei ist eine Menge ${\displaystyle O\subset \mathbb {Z} }$ offen, wenn sie leer ist oder für jedes ${\displaystyle a\in O}$ ein ${\displaystyle b>0}$ existiert, sodass ${\displaystyle N_{a,b}:=\{a+bn\mid n\in \mathbb {Z} \}\subseteq O.}$ Also ist jede nicht-leere offene Menge unendlich groß. Es kann gezeigt werden, dass dies eine Topologie definiert. Entscheidend ist, dass jedes ${\displaystyle N_{a,b}}$ auch abgeschlossen ist. Aus der Identität

${\displaystyle \mathbb {Z} \setminus \{-1,1\}=\bigcup _{p\,\mathrm {Primzahl} }N_{0,p}}$

wird aus der Annahme, dass die Primzahlen eine endliche Menge bilden, gefolgert, dass ${\displaystyle \{-1,1\}}$ offen ist, was damit aber eine unendlich mächtige Menge sein müsste.^[43]

Erdös’ kombinatorischer Beweis

Paul Erdös lieferte mehrere Beweise für die Unendlichkeit der Primzahlen. Einer davon zeigt über ein kurzes Argument den weiter unten diskutierten Satz von Euler über Primzahlen,^[44] und der andere über ein etwas schwächeres (aber schnelleres) kombinatorisches Argument die Unendlichkeit der Primzahlen: Ist ${\displaystyle \{p_{1},\dotsc ,p_{n}\}}$ die (vollständige) Menge aller Primzahlen, die kleiner als eine natürliche Zahl ${\displaystyle N}$ sind, so lässt sich jede Zahl kleiner oder gleich ${\displaystyle N}$ eindeutig als ein Produkt

${\displaystyle p_{1}^{e_{1}}\cdot p_{2}^{e_{2}}\dotsm p_{n}^{e_{n}}\cdot m^{2}}$

mit ${\displaystyle e_{j}\in \{0,1\}}$ und einer Quadratzahl ${\displaystyle m^{2}}$ schreiben. Dabei ist ${\displaystyle e_{j}}$ gleich 0, falls der Primfaktor in gerader Anzahl auftaucht und entsprechend 1, falls er in ungerader Anzahl in Erscheinung tritt. Damit gibt es ${\displaystyle 2^{n}}$ Möglichkeiten für die Wahl des Primzahlprodukts. Es folgt ${\displaystyle N\leq 2^{n}{\sqrt {N}}}$ und schließlich ${\displaystyle 2^{n}\geq {\sqrt {N}}}$. Durch hinreichend große Wahl von ${\displaystyle N}$ entsteht ein Widerspruch.^[45]

Washingtons Beweis mittels kommutativer Algebra

Ein Beweis von Lawrence C. Washington aus dem Jahr 1980 nutzt kommutative Algebra.^[46][47] Es wird ein abstrakter Satz verwendet, nämlich, dass ein Dedekindring mit nur endlich vielen Primidealen bereits ein Hauptidealring ist. Als solcher ist der Dedekindring dann ein faktorieller Ring, seine Elemente haben also eine eindeutige Zerlegung in Primelemente. Im Umkehrschluss bedeutet dies, dass ein Dedekindring mit keiner eindeutigen Primelementzerlegung unendlich viele Primideale haben muss. Bekannt ist, dass jeder Ganzheitsring ${\displaystyle {\mathcal {O}}_{K}}$ eines Zahlkörpers ${\displaystyle K}$ ein Dedekindring ist. Es kann gezeigt werden, dass für jedes Primideal ${\displaystyle {\mathfrak {p}}}$ höchstens ${\displaystyle [K:\mathbb {Q} ]}$ Primzahlen ${\displaystyle p}$ über ${\displaystyle {\mathfrak {p}}}$ liegen, also gewissermaßen zu ${\displaystyle {\mathfrak {p}}}$ „korrespondieren“. Dabei ist ${\displaystyle [K:\mathbb {Q} ]}$ der Grad der Körpererweiterung. Für den Beweis des Satzes des Euklid reicht es demnach aus, die Existenz eines solchen Dedekindrings mit fehlender Primelementzerlegung nachzuweisen. Ein Beispiel ist ${\displaystyle K=\mathbb {Q} ({\sqrt {-5}})}$ mit ${\displaystyle {\mathcal {O}}_{K}=\mathbb {Z} [{\sqrt {-5}}]}$, denn zum Beispiel gilt

${\displaystyle 6=2\cdot 3=(1-{\sqrt {-5}})(1+{\sqrt {-5}}).}$

Stärkere Resultate

Satz von Euler

Leonhard Euler konnte im Jahr 1737 zeigen, dass die Reihe der Kehrwerte aller Primzahlen divergiert, also^[48]

${\displaystyle \sum _{p{\text{ Primzahl}}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+{\frac {1}{19}}+\dotsb =\infty .}$

Dies bedeutet anschaulich, dass sich für jede noch so große Zahl immer (endlich viele) Primzahlen finden lassen, deren summierte Kehrwerte die gegebene Zahl überschreiten. Diese Aussage ist stärker als der Satz des Euklid, da sie die Unendlichkeit der Primzahlen impliziert, deren Unendlichkeit jedoch a priori nicht die Divergenz der Reihe: Beispielsweise gibt es unendlich viele ganze Zehnerpotenzen, aber es ist ${\displaystyle 1+{\tfrac {1}{10}}+{\tfrac {1}{100}}+{\tfrac {1}{1000}}+\dotsb =1{,}111\ldots ={\tfrac {10}{9}}<\infty .}$ Für den Beweis verwendete Euler das nach ihm benannte Euler-Produkt und führte sein Argument auf die Divergenz der harmonischen Reihe ${\displaystyle 1+{\tfrac {1}{2}}+{\tfrac {1}{3}}+{\tfrac {1}{4}}+\dotsb }$ zurück.^[49]

Im Jahr 1874 konnte Franz Mertens dieses Ergebnis verbessern, indem er ausrechnete, wie schnell die Summe in Abhängigkeit einer Abbruchschranke anwächst. Mertens zeigte, dass es eine Zahl ${\displaystyle M}$ gibt, sodass

${\displaystyle \sum _{p\leq x \atop p{\text{ Primzahl}}}{\frac {1}{p}}=\log(\log(x))+M+o(1),}$

wobei der von ${\displaystyle x}$ abhängige Fehler ${\displaystyle o(1)}$ für steigende Werte gegen 0 strebt.^[50] Die Funktion ${\displaystyle f(x)=\log(\log(x))}$ wächst zwar langsam an, ist jedoch unbeschränkt. In der Tat divergiert die Reihe ${\displaystyle {\tfrac {1}{2}}+{\tfrac {1}{3}}+{\tfrac {1}{5}}+{\tfrac {1}{7}}+{\tfrac {1}{11}}+{\tfrac {1}{13}}+\dotsb }$ entsprechend „langsam“: Ein Computer, der jede Nanosekunde einen neuen Summanden addiert, wäre nach ca. 15 Milliarden Jahren der Berechnung bei einer Zahl, die etwas größer als 4 ist.^[51]

Ebenfalls verwandt zu Euler’s Satz ist die Beobachtung

${\displaystyle \prod _{p\leq x \atop p{\text{ Primzahl}}}\left({\frac {1}{1-{\frac {1}{p}}}}\right)\geq \sum _{n\leq x}{\frac {1}{n}}\geq \log(x),\qquad x>2,}$

von James Joseph Sylvester aus dem Jahr 1888.^[52]

Dirichletscher Primzahlsatz

Im Jahr 1837 bewies Peter Dirichlet, dass jede arithmetische Progression natürlicher Zahlen bereits unendlich viele Primzahlen enthalten muss, wenn Startwert und der konstant hinzukommende Summand teilerfremd sind. Zum Beispiel enthält die Progression 7, 11, 15, 19, 23 … unendlich viele Primzahlen, da 7 und 4 teilerfremd sind. Dieses Resultat ist stärker als der Satz des Euklid, da dieser als Spezialfall aus dem Dirichletschen Primzahlsatz, angewendet auf die Progression 1, 2, 3, 4, 5 …, hervorgeht.

Der Beweis dieses Satzes ist eine typische Anwendung der analytischen Zahlentheorie. Er nutzt die Tatsache, dass Dirichletsche L-Funktionen an der Stelle ${\displaystyle s=1}$ nicht Null werden.^[53] Trotzdem findet das Resultat auch in der algebraischen Zahlentheorie Anwendung, zum Beispiel an einer kritischen Stelle im Beweis des Hasse-Minkowski-Prinzips.^[54]

Der Beweis des Satzes basiert auf einer Verallgemeinerung des Satzes von Euler. Genau genommen zeigte Dirichlet, dass die Reihe der Kehrwerte der Primzahlen in der arithmetischen Progression divergiert. Für teilerfremde ${\displaystyle N}$ und ${\displaystyle a}$ gilt also

${\displaystyle \sum _{p\,{\text{ Primzahl}} \atop p\equiv a{\pmod {N}}}{\frac {1}{p}}=\infty .}$

Der Dirichletsche Primzahlsatz konnte später von Carl Ludwig Siegel und Arnold Walfisz verschärft werden. Durch den Satz von Siegel-Walfisz wurde u. a. gezeigt, dass die Anzahl der Primzahlen in Progressionen mit gleichem Abstandsprinzip asymptotisch gleich häufig sind.^[55] Demnach enthalten z. B. die Progressionen 1, 1001, 2001, 3001, 4001, … und 7, 1007, 2007, 3007, 4007, … asymptotisch betrachtet gleich viele Primzahlen.

Eine modernere und noch stärkere Fassung des Dirichletschen Primzahlsatzes ist der Satz von Bombieri und Winogradow.

Bertrandsches Postulat

Das Bertrandsche Postulat sagt aus, dass zwischen jeder Zahl ${\displaystyle n\geq 2}$ und ihrem Doppelten mindestens eine Primzahl liegt. Wählt man etwa ${\displaystyle n=3}$, so liegt im Bereich ${\displaystyle 3<p\leq 6}$ die Primzahl ${\displaystyle p=5}$. Es ist benannt nach Joseph Bertrand, der es für alle Argumente ${\displaystyle 2\leq n\leq 3\,000\,000}$ zeigte.^[56] Erstmals vollständig bewiesen wurde dieses Resultat von Pafnuti Lwowitsch Tschebyschow. Es folgten weitere teils einfachere Beweise durch Paul Erdös und Srinivasa Ramanujan,^[56] der dabei auch die Ramanujan-Primzahlen betrachtete, die einer gewissen Ungleichung genügen.^[57] Im Gegensatz zum Satz des Euklid, der aus dem Postulat durch beliebig große Wahl von ${\displaystyle n}$ folgt, macht das Betrandsche Postulat eine erste „starke“ Häufigkeitsanalyse über die Primzahlen. Zwar kann gezeigt werden, dass zwischen beliebig groß werdenden Primzahlen beliebig große Lücken entstehen können, aber das Postulat gibt eine Schranke für die Lücke in Abhängigkeit der Größe der Primzahl: Ist ${\displaystyle p}$ eine Primzahl, so gilt für die darauf folgende Primzahl ${\displaystyle q}$ die Abschätzung ${\displaystyle q<2p}$.^[56]

Verwandte Fragestellungen um die Dichte der Primzahlen sind mitunter deutlich schwieriger zu beweisen. Es wird vermutet, dass zwischen zwei benachbarten positiven Quadratzahlen stets eine Primzahl liegt. Diese Legendresche Vermutung konnte jedoch bisher nicht bewiesen werden. Allerdings konnte Albert Ingham 1937 beweisen, dass sich für hinreichend große ${\displaystyle n}$ zwischen den benachbarten Kubikzahlen ${\displaystyle n^{3}}$ und ${\displaystyle (n+1)^{3}}$ stets eine Primzahl befindet.^[58]

Primzahlsatz

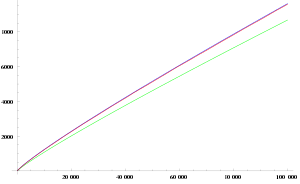
Die untere Schranke des Satzes des Euklid für die Anzahl der Primzahlen bis zu einer Größe ${\displaystyle x}$ kann deutlich verbessert werden. Ende des 19. Jahrhunderts gelang es Jacques Hadamard und Charles-Jean de La Vallée Poussin unabhängig voneinander zu zeigen, dass die Anzahl der Primzahlen ${\displaystyle \pi (x)}$ unter einer positiven Schranke ${\displaystyle x}$ ungefähr gleich ${\displaystyle {\tfrac {x}{\log(x)}}}$ ist, und dass der relative Fehler in dieser Schätzung für unbeschränkt wachsende ${\displaystyle x}$ gegen 0 strebt. Es gilt also

${\displaystyle \lim _{x\to \infty }{\frac {\pi (x)}{\frac {x}{\log(x)}}}=1.}$

Dabei ist ${\displaystyle \log(x)}$ der natürliche Logarithmus von ${\displaystyle x}$. Oft wird bei der Formulierung des Primzahlsatzes statt der Funktion ${\displaystyle {\tfrac {x}{\log(x)}}}$ auch der Integrallogarithmus gewählt. Aus ${\displaystyle \lim _{x\to \infty }{\tfrac {x}{\log(x)}}=\infty }$ ergibt sich der Satz des Euklid als direkte Folgerung. Als eine weitere Folgerung des Primzahlsatzes ergibt sich eine Möglichkeit, zu schätzen, wie groß die zehnte, hundertste, tausendste oder allgemein ${\displaystyle n}$-te Primzahl ist, wenn man sie in ihrer aufsteigenden Folge 2, 3, 5, 7, … betrachtet. Das Gesetz lautet ${\displaystyle p_{n}\sim n\log(n)}$ für die ${\displaystyle n}$-te Primzahl ${\displaystyle p_{n}}$, das heißt, dass ${\displaystyle p_{n}}$ auf lange Sicht gleich schnell wächst wie ${\displaystyle n\log(n)}$. Beispielsweise ist ${\displaystyle p_{10\,000}=104\,729}$^[59] und ${\displaystyle 10\,000\log(10\,000)\approx 92\,103}$.

Im Gegensatz zu Euklids Beweis der Unendlichkeit der Primzahlen verwendeten die ersten Beweise der Primzahlsätze analytische Methoden, die auf nullstellenfreien Regionen von L-Funktionen fußen.^[60] Es wurden jedoch von Paul Erdös und Atle Selberg auch elementare Beweise des Primzahlsatzes gefunden, die ohne analytische Methoden auskommen.^[61] Ein weiterer elementarer Beweis stammt von Florian K. Richter aus dem Jahr 2021.^[62]

Die Frage, wie groß die Abweichung der Abschätzung des Primzahlsatzes von der eigentlichen Zählfunktion ist, ist Gegenstand der Riemannschen Vermutung.^[63]

Satz von Chen

Im Jahr 1966 gelang dem chinesischen Mathematiker Chen Jingrun der Nachweis folgender „Annäherung“ an die bisher unbewiesene Goldbachsche Vermutung:^[64]

Jede hinreichend große gerade Zahl kann als Summe einer Primzahl und einer Zahl mit höchstens zwei Primfaktoren geschrieben werden.

Dies impliziert insbesondere den Satz des Euklid, da es bei nur endlich vielen Primzahlen keine Möglichkeit gäbe, beliebig große Zahlen so darzustellen. In der Tat, wäre ${\displaystyle P}$ die „größte“ Primzahl, so wäre die größte Summe aus Primzahl und Produkt zweier Primzahlen gegeben durch ${\displaystyle P+P^{2}<\infty }$.

Der Ausdruck „hinreichend groß“ im Satz von Chen bedeutet, dass es eine minimale Zahl gibt (die aber sehr groß sein kann!), so dass die Aussage ab dort immer stimmt. Knapp 50 Jahre nach Chens Beweis, im Jahr 2015, fand Tomohiro Yamada eine explizite Schranke, ab der der Satz von Chen definitiv anwendbar ist.^[65]

Jede gerade Zahl größer als ${\displaystyle e^{e^{36}}}$ kann als Summe einer Primzahl und einer Zahl mit höchstens zwei Primfaktoren geschrieben werden.

Dabei ist ${\displaystyle e=2{,}7182818\dots }$ die Eulersche Zahl.

Satz von Green-Tao

Im Jahr 2004 zeigten Ben Green und Terence Tao den Satz von Green-Tao, dass es in der Folge der Primzahlen beliebig lange arithmetische Progressionen gibt.^[66] Zum Beispiel ist 3, 5, 7 eine Progression von Primzahlen der Länge 3, da alle benachbarten Zahlen den gleichen Abstand haben. Die längste bekannte (Stand 2020) arithmetische Folge von Primzahlen hat die Länge 27.^[67] Explizit ist sie gegeben durch

${\displaystyle 224\,584\,605\,939\,537\,911+18\,135\,696\,597\,948\,930\,n,\,\,\,n=0,\dotsc ,26.}$

Verwandte Probleme

Während durch den Satz des Euklid bekannt ist, dass die Menge der Primzahlen unendlich groß ist, erweisen sich Fragestellungen nach der Unendlichkeit gewisser Teilmengen von Primzahlen mitunter schwierig.

Primzahlzwillinge

Zum Beispiel ist die Frage, ob es unendlich viele Primzahlzwillinge gibt, bis heute nicht beantwortet.^[68] Ein Paar ${\displaystyle p<q}$ von Primzahlen heißt Zwilling, wenn ${\displaystyle q-p=2}$ gilt, sich beide also bloß um 2 unterscheiden. Die ersten Primzahlzwillinge sind

${\displaystyle (3,5),(5,7),(11,13),(17,19),(29,31),(41,43),\dotsc .}$

Mit Hilfe des Brunschen Siebs konnte von Viggo Brun gezeigt werden, dass es eine Konstante ${\displaystyle C>0}$ gibt, sodass für jedes ${\displaystyle x>2}$ und die Anzahl ${\displaystyle \pi _{2}(x)}$ aller Primzahlzwillinge bis ${\displaystyle x}$ gilt:^[69]

${\displaystyle \pi _{2}(x)\leq Cx\left({\frac {\log(\log(x))}{\log(x)}}\right)^{2}}$

Als Folgerung ergibt sich, dass die Reihe aller Kehrwerte der Primzahlzwillinge konvergiert,^[70] also

${\displaystyle \left({\frac {1}{3}}+{\frac {1}{5}}\right)+\left({\frac {1}{5}}+{\frac {1}{7}}\right)+\left({\frac {1}{11}}+{\frac {1}{13}}\right)+\left({\frac {1}{17}}+{\frac {1}{19}}\right)+\left({\frac {1}{29}}+{\frac {1}{31}}\right)+\dotsb <\infty ,}$

und zwar gegen die Brunsche Konstante ${\displaystyle B\approx 1{,}90216.}$^[71] Damit ist ein Beweis der Unendlichkeit der Menge aller Primzahlzwillinge analog zum Satz von Euler nicht möglich. Nicht-triviale untere Schranken von ${\displaystyle \pi _{2}}$ sind bis heute lediglich Gegenstand von Vermutungen. So wurde 1922 von Godfrey Harold Hardy und John Edensor Littlewood vermutet,^[69] dass sich die Anzahl ${\displaystyle \pi _{2}(x)}$ der Primzahlzwillinge unter einer wählbaren Schranke ${\displaystyle x}$ asymptotisch verhält wie

${\displaystyle \pi _{2}(x)\sim 2C_{1}{\frac {x}{\log ^{2}(x)}}\sim 2C_{1}\int _{2}^{x}{\frac {\mathrm {d} t}{\log ^{2}(t)}}.}$

Dabei ist

${\displaystyle C_{1}=\prod _{p\geq 3,\ \mathrm {Primzahlen} }\left(1-{\frac {1}{(p-1)^{2}}}\right)=0{,}66016\,18158\,46869\,57392\,78121\,10014\dots .}$

Dies hätte als Konsequenz, dass es unendlich viele Primzahlzwillinge gibt, da der Term ${\displaystyle x}$ aufgrund des langsamen Wachstums der Logarithmen viel schneller wächst als der quadrierte Logarithmus ${\displaystyle \log ^{2}(x).}$ Auch die Frage, ob es unendlich viele Primzahlvierlinge oder -sechslinge gibt, ist ungeklärt. Allerdings konnten Daniel Goldston, Cem Yıldırım und János Pintz nachweisen, dass es auf gewisse Weise langfristig immer wieder „relativ dünn“ zwischen Primzahlen wird, im Sinne von^[72][73]

${\displaystyle \liminf _{n\to \infty }{\frac {p_{n+1}-p_{n}}{\log(p_{n})}}=0.}$

Dabei bedeutet das Symbol ${\displaystyle \liminf }$ Limes inferior. Seitdem wurde stark daran gearbeitet, die Abschätzungen der Abstände kleiner werden zu lassen. Schließlich gelang Yitang Zhang ein Durchbruch, indem er bewies, dass es unendlich oft vorkommt, dass zwei benachbarte Primzahlen näher als ${\displaystyle 70\,000\,000}$ voneinander entfernt sind.^[74] Es gilt also

${\displaystyle \liminf _{n\to \infty }(p_{n+1}-p_{n})<70\,000\,000.}$

Damit wurde erstmals gezeigt, dass Primzahlabstände einen festen Abstand immer wieder unterschreiten. Das Resultat wurde 2015 von James Maynard auf den Abstand 600 verbessert.^[75] Die Primzahlzwillings-Vermutung ist äquivalent zu

${\displaystyle \liminf _{n\to \infty }(p_{n+1}-p_{n})=2.}$

Fermat- und Mersenne-Primzahlen

Auch die Frage, ob unendlich viele Zahlen der Folgen ${\displaystyle M_{p}=2^{p}-1}$ (mit ${\displaystyle p}$ Primzahl) bzw. ${\displaystyle F_{n}=2^{2^{n}}+1}$ wieder Primzahlen sind, ist ungeklärt. Während jedoch angenommen wird, dass es unendlich viele Mersenne-Primzahlen gibt, wird davon ausgegangen, dass es außer ${\displaystyle F_{0},F_{1},F_{2},F_{3}}$ und ${\displaystyle F_{4}}$ keine weitere Fermat-Primzahl gibt. So konnte schon Leonhard Euler zeigen, dass ${\displaystyle F_{5}}$ durch 641 teilbar ist. Damit widerlegte er die Vermutung Fermats, dass jede der Zahlen ${\displaystyle F_{n}}$ eine Primzahl sei.^[76]

Literatur

• Die Elemente von Euklid. In: Ostwalds Klassiker der exakten Wissenschaften. Verlag Europa-Lehrmittel, 4. Auflage, 2015.
• Benno Artmann: Euclid – The creation of mathematics. Springer-Verlag, New York, 1999.
• Romeo Meštrović: Euclid’s theorem on the infinitude of primes: a historical survey of its proofs (300 B.C. – 2017) and another new proof. 2018.
• Paul Pollack: Not Always Burried Deep: Selections from Analytic and Combinatorial Number Theory. In: American Mathematical Society. 2009.
• Paulo Ribenboim: The little book of bigger primes. Springer-Verlag, New York, 2004.

Weblinks

Wikibooks: Beweis zum Satz von Euklid – Im Beweisarchiv auf Wikibooks finden sich weitere Beweise für die Existenz von unendlich vielen Primzahlen.

• Video: Satz des Euklid. Pädagogische Hochschule Heidelberg (PHHD) 2012, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/19866.

Einzelnachweise

1. ↑ Olivier Bordellés: Arithmetic Tales. Springer-Verlag, 2020, S. 45.
2. ↑ Euclid’s Elements of Geometry. In: Euclidis Elementa. Edidit et Latine interpretatus est I.L. Heiberg, in aedibus B.G. Teubneri, 1883–1885, Übersetzung von Richard Fitzpatrick, S. 271.
3. ↑ Die Elemente von Euklid. In: Ostwalds Klassiker der exakten Wissenschaften. Verlag Europa-Lehrmittel, 4. Auflage, 2015, S. 204–205.
4. ↑ Rudolf Haller (Übersetzer): Euklid: Elemente Stoicheia. Markgröningen : Edition Opera-Platonis, 2010, abgerufen am 15. Januar 2021. 
5. ↑ Die Elemente von Euklid. In: Ostwalds Klassiker der exakten Wissenschaften. Verlag Europa-Lehrmittel, S. 160.
6. ↑ Peter Schreiber, Sonja Brentjes: Euklid. Teubner Verlagsgesellschaft, 1987, S. 41.
7. ↑ Victor J. Katz: A History of Mathematics. An Introduction. Second Edition, Addison Wesley Longman, 1998, S. 87.
8. ↑ ^{a b c d} Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, S. 2.
9. ↑ Tom M. Apostol: Introduction to Analytic Number Theory. Springer, S. 16–17.
10. ↑ Michael Hardy, Catherine Woodgold: Prime Simplicity. In: Mathematical Intelligencer. Vol. 31, No. 4, 2009, S. 44–52.
11. ↑ Torkel Franzén: Inexhaustibility. A Non-exhaustive Treatment. A. K. Peters, Ltd., 2004, S. 101.
12. ↑ Benno Artmann: Euclid – The creation of mathematics. Springer, 1999, S. 279–281.
13. ↑ Gerald Tenenbaum, Michel Mendès France: The Prime Numbers and Their Distribution, Student Mathematical Library, Vol. 6, AMS, S. 2.
14. ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, S. 3–10.
15. ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, S. 4.
16. ↑ The top twenty primorial primes. Abgerufen am 1. Januar 2021.
17. ↑ The Largest Known Primes – A Summary. Abgerufen am 1. Januar 2021.
18. ↑ M. Dalezman: From 30 to 60 is Not Twice as Hard. In: Mathematics Magazine 73. 2000, S. 151–153.
19. ↑ V. A. Lebesgue: Jour. de Math. 8 (1843), S. 51, note; Exercises d’analyse numérique. 1859, S. 91.
20. ↑ V. A. Lebesgue: Remarques diverses sur les nombres premiers. In: Nouv. Ann. Math. 15, 1856, 130–134, 236–239.
21. ↑ V. A. Lebesgue: Exercises d’analyse numérique. Paris, 1859, 91–95, 103–104, 145–146.
22. ↑ V. A. Lebesgue: Jour. de Math. (2) 7, 1862, S. 417.
23. ↑ J. J. Sylvester: On the theorem that an arithmetical progression which contains more than one, contains an infinite number of prime numbers. In: Proc. London Math. Soc. 4, 1871, S. 7–8.
24. ↑ J. J. Sylvester: On certain inequalities relating to prime numbers. In: Nature. 38, 1888, S. 259–262.
25. ↑ L. Kronecker: Vorlesungen über Zahlentheorie. I, Teubner, Leipzig 1901.
26. ↑ E. E. Kummer: Neuer elementarer Beweis des Satzes, dass die Anzahl aller Primzahlen eine unendliche ist. In: Monatsber. Preuss. Akad. Wiss. Berlin 1878/79, S. 777–778.
27. ↑ G. Pólya: Arithmetische Eigenschaften der Reihenentwicklungen rationaler Funktionen. In: Journal für die reine und angewandte Mathematik. 151, 1921, S. 1–31.
28. ↑ R. Bellman: A note on relatively prime sequences. In: Bull. Amer. Math. Soc. 53, 1947, S. 778–779.
29. ↑ A. Weil: Number theory for beginners. Springer-Verlag, New York 1979.
30. ↑ A. Granville: Prime Numbers, Part 1: Infinitely many primes; non-analytic methods. In: Course Notes. 2007.
31. ↑ A. Granville: Different approaches to the distribution of primes. In: Milan J. Math. 78, 2009, S. 1–25.
32. ↑ Romeo Mestrovic: Euclid’s theorem on the infinitude of primes: A historical survey of its proofs (300 B.C. – 2017). S. 7–8.
33. ↑ P. H. Fuss: Correspondance mathematique et physique de quelques celebres geometres du XVIII ́eme siecle. St. Petersbourg 1843, S. 32–34. Verfügbar im Euler-Archiv (PDF; 75,1 kB), abgerufen am 1. Januar 2021.
34. ↑ Martin Aigner, Günter M. Ziegler: Das Buch der Beweise. 2. Auflage, Springer, S. 3–4.
35. ↑ Martin Aigner, Günter M. Ziegler: Das Buch der Beweise. 2. Auflage, Springer, S. 4.
36. ↑ Paul Pollack: Not Always Buried Deep – Selections from Analytic and Combinatorial Number Theory. S. 3.
37. ↑ J. Braun: Das Fortschreitungsgesetz der Primzahlen durch eine transzendente Gleichung exakt dargestellt. In: JBer. Gymnasium Trier. Wiss. Beilage, 1899, 1–96.
38. ↑ Miklós Laczkovich: On Lambert’s Proof of the Irrationality of π. In: The American Mathematical Monthly. Band 104, Nr. 5, Mai 1997, S. 439–443, doi:10.2307/2974737. 
39. ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, S. 74.
40. ↑ ^{a b} Romeo Mestrovic: Euclid’s theorem on the infinitude of primes: A historical survey of its proofs (300 B.C. – 2017). S. 23.
41. ↑ Neville Robbins: Some identities connecting partition functions to other number theoretic functions. In: Rocky Mountains Journal. No. 29, 1999, S. 342–343.
42. ↑ Harry Fürstenberg: On the infinitude of primes. In: American Mathematical Monthly. Bd. 62, Nr. 5, 1955, S. 353.
43. ↑ Martin Aigner, Günter M. Ziegler: Das Buch der Beweise. 2. Auflage, Springer, S. 5.
44. ↑ Martin Aigner, Günter M. Ziegler: Das Buch der Beweise. 2. Auflage, Springer, S. 6.
45. ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, S. 39.
46. ↑ Paulo Ribenboim: The little book of bigger primes. Springer-Verlag, New York 2004, S. 8.
47. ↑ Paul Pollack: Not Always Buried Deep – Selections from Analytic and Combinatorial Number Theory. S. 17.
48. ↑ Lokenath Debnath: The legacy of Leonhard Euler. A Tricentennial Tribute. S. 65.
49. ↑ Lokenath Debnath: The legacy of Leonhard Euler. A Tricentennial Tribute. S. 213.
50. ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, S. 8.
51. ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, S. 40.
52. ↑ J. J. Sylvester: On certain inequalities relating to prime numbers. In: Nature 38. 1888, S. 259–262.
53. ↑ Jean Pierre Serre: A course in arithmetic. Springer-Verlag, New York 1973, S. 73.
54. ↑ Jean Pierre Serre: A course in arithmetic. Springer-Verlag, New York 1973, S. 25.
55. ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, S. 114.
56. ↑ ^{a b c} Martin Aigner, Günter M. Ziegler: Das Buch der Beweise. 2. Auflage, Springer, S. 7.
57. ↑ Ramanujan: A proof of Bertrand’s postulate. In: Journal of the Indian Mathematical Society. 11, 1919, 181–182.
58. ↑ Albert E. Ingham: On the difference between consecutive primes. In: The Quarterly Journal of Mathematics. Oxford Series 8, 1937, Nr. 1, S. 255–266.
59. ↑ Liste der ersten zehntausend Primzahlen. Abgerufen am 1. Januar 2021.
60. ↑ Gérald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. In: AMS. Vol. 163, S. 261 ff.
61. ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. In: AMS. Vol. 163, S. 12.
62. ↑ Florian K. Richter: A new elementary proof of the Prime Number Theorem, Bulletin of the London Mathematical Society, Volume 53, Issue 5, S. 1365–1375 arxiv:2002.03255.
63. ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. In: AMS. Vol. 163, S. 271.
64. ↑ J. R. Chen: On the representation of a large even integer as the sum of a prime and the product of at most two primes. In: Kexue Tongbao. 11 (9), 1966, S. 385–386.
65. ↑ Tomohiro Yamada: Explicit Chen’s theorem. PDF (ArXiv), abgerufen am 1. Januar 2021.
66. ↑ Ben Green, Terence Tao: The primes contain arbitrarily long arithmetic progressions. In: Annals of Mathematics. Serie 2, Bd. 167, Nr. 2, 2008, S. 481–547.
67. ↑ PrimeGrid’s AP27 Search. (PDF; 219 kB) In: PrimeGrid.com. Abgerufen am 1. Januar 2021 (englisch). 
68. ↑ John Nash, Michael Rassias (Hrsg.): Open Problems in Mathematics. Springer, S. 498.
69. ↑ ^{a b} G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. In: AMS. Vol. 163, S. 71.
70. ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, S. 182.
71. ↑ S. R. Finch: Mathematical Constants. In: Encyclopedia of Mathematics and its Applications. 94, Cambridge University Press, 2003, S. 133.
72. ↑ D. A. Goldston, Y. Motohashi, J. Pintz, C. Y. Yıldırım: Small Gaps between Primes Exist. In: Japan Academy. Proceedings. Series A. Mathematical Sciences. 82(4), S. 61–65.
73. ↑ D. A. Goldston, J. Pintz, C. Y. Yıldırım: Small gaps between primes II (Preliminary). Preprint, 8. Februar 2005.
74. ↑ Yitang Zhang: Bounded gaps between primes. In: Annals of Mathematics. 179(3), 2014, S. 1121–1174.
75. ↑ James Maynard: Small gaps between primes. In: Annals of Mathematics. Second Series, 181, 2015, S. 383–413.
76. ↑ Leonhard Euler: Observationes de theoremate quodam Fermatiano aliisque ad numeros primos spectantibus. [E26]. In: Commentarii academiae scientiarum Petropolitanae. 6 (1732/33), St. Petersburg 1738, S. 103–107, hier S. 104. Nachdruck in Opera Omnia, Bd. 1/2, S. 1–5. Englische Übersetzung von Ian Bruce: Observations concerning a certain theorem of Fermat and other considerations regarding prime numbers. (PDF; 98 kB) bzw. von David Zhao: Oberservations on a certain theorem of Fermat and on others regarding prime numbers.