2-functor

In mathematics, specifically, in category theory, a 2-functor is a morphism between 2-categories.^[1] They may be defined formally using enrichment by saying that a 2-category is exactly a Cat-enriched category and a 2-functor is a Cat-functor.^[2]

Explicitly, if C and D are 2-categories then a 2-functor ${\displaystyle F\colon C\to D}$ consists of

• a function ${\displaystyle F\colon {\text{Ob}}C\to {\text{Ob}}D}$, and
• for each pair of objects ${\displaystyle c,c'\in {\text{Ob}}C}$, a functor ${\displaystyle F_{c,c'}\colon {\text{Hom}}_{C}(c,c')\to {\text{Hom}}_{D}(Fc,Fc')}$

such that each ${\displaystyle F_{c,c'}}$ strictly preserves identity objects and they commute with horizontal composition in C and D.

See ^[3] for more details and for lax versions.

References

• v
• t
• e

Category theory

Key concepts

Key concepts Category Abelian Additive Concrete Pre-abelian Preadditive Bicategory Adjoint functors CCC Commutative diagram End Exponential Functor Kan extension Morphism Natural transformation Universal property Universal constructions Limits Terminal objects Products Equalizers Kernels Pullbacks Inverse limit Colimits Initial objects Coproducts Coequalizers Cokernels and quotients Pushout Direct limit Algebraic categories Sets Relations Magmas Groups Abelian groups Rings (Fields) Modules (Vector spaces) Constructions on categories Free category Functor category Kleisli category Opposite category Quotient category Product category Comma category Subcategory

Higher category theory

Key concepts Categorification Enriched category Higher-dimensional algebra Homotopy hypothesis Model category Simplex category String diagram Topos n-categories Weak n-categories Bicategory (pseudofunctor) Tricategory Tetracategory Kan complex ∞-groupoid ∞-topos Strict n-categories 2-category (2-functor) 3-category Categorified concepts 2-group 2-ring En-ring (Traced)(Symmetric) monoidal category n-group n-monoid

• Category
• Outline
• Glossary

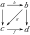This category theory-related article is a stub. You can help Wikipedia by expanding it.

• v
• t
• e