Legendren polynomi

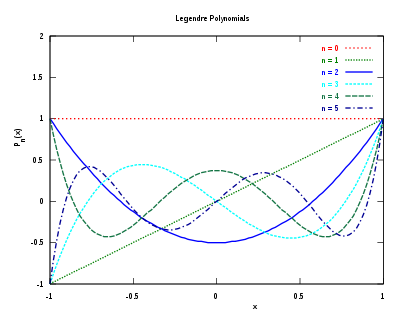
Legendren polynomit eli Legendren funktiot ovat joukko polynomeja, jotka muodostavat ortogonaalisen joukon. Legendren polynomeja käytetään hyvin monenlaisissa yhteyksissä niin fysiikassa kuin matematiikassakin. Vaikka Legendren polynomit ovat nimensä mukaisesti polynomeja, luonteensa vuoksi niitä pidetään usein erikoisfunktioina. Legendren polynomit ovat erikoistapaus Legendren liittofunktioista.

Legendren polynomeja syntyy Legendren differentiaaliyhtälön

${\displaystyle (1-x^{2}){\frac {d^{2}y}{dx^{2}}}-2x{\frac {dy}{dx}}+n(n+1)y=0}$

ratkaisuina, kun yhtälön ratkaisemiseen käytetyn potenssisarjan kertoimet ovat kertoimesta ${\displaystyle a_{n}}$ lähtien nollia. Viisi ensimmäistä Legendren polynomia ovat

${\displaystyle P_{0}(x)=1\,}$

${\displaystyle P_{1}(x)=x\,}$

${\displaystyle P_{2}(x)={\frac {1}{2}}(3x^{2}-1)\,}$

${\displaystyle P_{3}(x)={\frac {1}{2}}(5x^{3}-3x)\,}$

${\displaystyle P_{4}(x)={\frac {1}{8}}(35x^{4}-30x^{2}+3)\,}$

${\displaystyle P_{5}(x)={\frac {1}{8}}(63x^{5}-70x^{3}+15x)\,}$

(Huomaa, kuinka parittoman ${\displaystyle n}$:n polynomeissa esiintyy vain parittomia ${\displaystyle x}$:n potensseja ja parillisissa parillisia.) Legendren polynomit ovat ortogonaalisia välillä ${\displaystyle [-1,1]}$, sillä minkä tahansa kahden polynomiin sisätulo

${\displaystyle \langle P_{n},P_{m}\rangle =\int _{-1}^{1}P_{n}(x)P_{m}(x)dx=0}$

aina kun ${\displaystyle n\neq m}$. Muiden ortogonaalisten polynomien tapaan Legendren polynomeille on olemassa polynomeja generoiva Rodriguesin kaava. ${\displaystyle n}$:s Legendren polynomi saadaan laskettua kaavalla

${\displaystyle P_{n}(x)={\frac {1}{2^{n}n!}}{\frac {d^{n}}{dx^{n}}}[(x^{2}-1)^{n}]}$,

mutta tämä on yleensä työlästä. Tehokkaampaa on käyttää rekursiokaavaa

${\displaystyle (n+1)P_{n+1}(x)=(2n+1)xP_{n}(x)-nP_{n-1}(x)\,}$

jolla ${\displaystyle (n+1)}$:s polynomi saadaan laskettua kun kaksi edellistä tunnetaan. Koska Legendren polynomit ovat ortogonaalisia, ne muodostavat funktioavaruuden kannan ja tämän vuoksi niitä voidaan käyttää muiden funktioiden ilmaisemiseen sarjakehitelmän avulla. Muita vastaavia tapoja ovat Taylorin ja Fourier'n sarjat. Funktiota ${\displaystyle f(x)}$ vastaava Legendren sarjakehitelmä on muotoa

${\displaystyle f(x)=c_{0}P_{0}(x)+c_{1}P_{1}(x)+c_{2}P_{2}(x)+\ldots =\sum _{k=0}^{\infty }c_{k}P_{k}(x)}$.

Tässä esiintyvät kertoimet ${\displaystyle c_{k}}$ saadaan laskettua Fourier'n sarjojen tapaan integroimalla

${\displaystyle c_{k}={\frac {2k+1}{2}}\int _{-1}^{1}f(x)P_{k}(x)dx}$

Legendren polynomikannassa kehitetty sarja on käyränsovituksessa erityisen tehokas, sillä riittävän säännöllisille funktioille kehitelmä antaa hyvän approksimaation jo varsin vähäisellä määrällä termejä. Lisäksi Taylorin sarjasta poiketen uusien termien ottaminen mukaan sovitukseen ei muuta jo laskettujen termien kertoimien ${\displaystyle c_{k}}$ arvoa, eikä sovitusta tarvitse siis tehdä alusta alkaen uudestaan.

Usein Legendren polynomit kirjoitetaan tekemällä sijoitus ${\displaystyle x=\cos \theta }$. Tämä on ongelmatonta, koska ortogonaalisuusväli ${\displaystyle [-1,1]}$ on sama kuin kosinin arvojoukko. Trigonometristen laskusääntöjen vuoksi polynomit saavat hieman poikkeavan muodon, eikä kyseessä enää tietysti ole polynomi vaan muu funktio. Viisi ensimmäistä Legendren polynomia ovat näin kirjoitettuna

${\displaystyle P_{0}(\cos \theta )=1\,}$

${\displaystyle P_{1}(\cos \theta )=\cos \theta \,}$

${\displaystyle P_{2}(\cos \theta )={\frac {1}{4}}(1+3\cos(2\theta ))\,}$

${\displaystyle P_{3}(\cos \theta )={\frac {1}{8}}(3\cos(\theta )+5\cos(3\theta ))\,}$

${\displaystyle P_{4}(\cos \theta )={\frac {1}{64}}(9+20\cos(2\theta )+35\cos(4\theta )),}$

${\displaystyle P_{5}(\cos \theta )={\frac {1}{128}}(30\cos(\theta )+35\cos(3\theta )+63\cos(5\theta ))\,}$

Näitä esitysmuotoja suositaan erityisesti fysiikassa.

• Jalava, Väinö: Johdatus funktionaalianalyysiin. Opintomoniste 95. Tampere: TTKK, 1983. ISBN 951-720-831-6.