Divergence (analyse vectorielle)

Pour les articles homonymes, voir Divergence.

En géométrie, la divergence d'un champ de vecteurs est un opérateur différentiel mesurant le défaut de conservation du volume sous l'action du flot de ce champ.

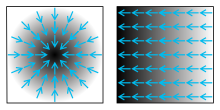
L'opérateur divergence est un outil d'analyse vectorielle qui mesure, pour faire simple, si un champ vectoriel « rentre » ou « sort » d'une zone de l'espace, comme ce que l’on peut observer sur un diagramme de lignes de champ. Il donne donc une information très liée aux sources qui créent le champ. Les équations de continuité permettent de comprendre intuitivement cette notion : la divergence mesure en effet localement les variations de densité de flux. On retrouve cette grandeur, macroscopiquement cette fois, dans les valeurs de diffusion de particule ou de chaleur par exemple. Ainsi, en un point, si la divergence est nulle, alors la densité ne varie pas ; si elle est positive en ce point, alors il y a diffusion.

En mécanique des fluides, si un fluide rentre dans un tube compressible avec davantage de force qu'il n'en sort à l'autre extrémité, le tube aura tendance à voir sa pression interne augmenter, et donc aussi son volume. La divergence ne caractérise cependant pas le comportement du tube, mais bien les caractéristiques du flux de matière, susceptibles d'influer sur le volume traversé.

Plus précisément, soit ${\displaystyle t\mapsto \phi _{t}(x)}$ la trajectoire du champ X issue de x.

Ces trajectoires s'organisent en une famille de transformations ${\displaystyle x\mapsto \phi _{t}(x)}$ (le flot de X), et pour tout domaine D on a

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {vol} (\phi _{t}(D))_{\vert t=0}=\int _{D}\operatorname {div} X\mathrm {d} \mathbf {x} }$

Un champ à divergence nulle est un champ qui conserve le volume, tel le champ des vecteurs vitesse d'un écoulement incompressible.

Ainsi, div X est une fonction à valeurs réelles qui mesure la variation première du volume le long des trajectoires dudit champ.

En raison de son utilisation dans les calculs de flux de champ de vecteurs, la divergence intervient en physique pour exprimer des lois de conservation ainsi que pour la formulation locale des lois physiques faisant intervenir un champ suivant une loi en carré inverse de la distance. La divergence est notamment utilisée dans les équations de la mécanique des fluides ou les équations de Maxwell.

Des définitions plus précises sont données dans le corps de l'article.

Divergence d'un champ de vecteurs

L'opérateur divergence est un opérateur différentiel linéaire de degré 1, défini sur les champs de vecteurs et à valeurs dans les fonctions.

Définition en dimension 3

En dimension 3 et en coordonnées cartésiennes, la divergence d'un champ de vecteurs ${\displaystyle {\vec {A}}={\begin{pmatrix}A_{x}\\A_{y}\\A_{z}\end{pmatrix}}}$ a pour expression^[1]

${\displaystyle \operatorname {div} {\vec {A}}={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}}$

Formellement, l'opérateur divergence appliqué à un champ vectoriel ${\displaystyle {\vec {A}}}$ peut s'interpréter comme produit scalaire du vecteur nabla ${\displaystyle {\vec {\nabla }}}$ par le vecteur ${\displaystyle {\vec {A}}}$.

${\displaystyle {\vec {\nabla }}\cdot {\vec {A}}=\operatorname {div} {\vec {A}}={\frac {\partial {A_{x}}}{\partial {x}}}+{\frac {\partial {A_{y}}}{\partial {y}}}+{\frac {\partial {A_{z}}}{\partial {z}}}}$

Cette définition a le désavantage d'être dépendante du choix d'une base orthonormée.

Interprétation heuristique concernant la variation du volume

Le flot du champ A est approximativement (pour t petit) donné par

${\displaystyle (x,y,z)\mapsto F_{t}(x,y,z)=(x,y,z)+tA(x,y,z)}$

Le volume de l'image par ${\displaystyle F_{t}}$ d'un « petit » pavé de centre (x,y,z) est multiplié par le déterminant de la matrice jacobienne de ${\displaystyle F_{t}}$. Mais la dérivée par rapport à t de ce déterminant, pour t=0 est précisément

${\displaystyle {\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}}$

Justification rigoureuse de l'interprétation

Elle utilise les formes différentielles. Dans ${\displaystyle \mathbb {R} ^{3}}$ le volume d'un domaine s'obtient en intégrant sur ce domaine la forme différentielle ${\displaystyle \mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z}$. Soit ${\displaystyle \phi _{t}}$ le flot du champ A.

La variation infinitésimale du volume est alors

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\phi _{t}^{\ast }(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)_{\mid t=0}}$

C'est par définition la dérivée de Lie : ${\displaystyle L_{A}(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)}$ de ${\displaystyle \mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z}$.

On vérifie que

${\displaystyle L_{A}(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)=\left({\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\right)(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)}$

(voir plus bas la démonstration en dimension n de cette identité).

En particulier, le flot de ${\displaystyle A}$ conserve le volume (c’est-à-dire ${\displaystyle \mathrm {vol} (\varphi _{t}(D))=\mathrm {vol} (D)}$ pour tout domaine ${\displaystyle D}$ de ${\displaystyle \mathbb {R} ^{3}}$) si et seulement si la divergence est partout nulle. Le volume augmente si la divergence est positive, diminue si elle est négative.

Ce calcul montre aussi que la divergence ne dépend pas de la structure euclidienne de l'espace, mais seulement de l'élément de volume.

Exemples

La divergence du champ ${\displaystyle x{\frac {\partial }{\partial x}}+y{\frac {\partial }{\partial y}}+z{\frac {\partial }{\partial z}}}$ (champ radial) est constante (égale à 3) (le flot de ce champ est formé d'homothéties, qui multiplient les volumes par une constante).

La divergence du champ ${\displaystyle y{\frac {\partial }{\partial x}}-x{\frac {\partial }{\partial y}}}$ est nulle (son flot est formé de rotations).

En mécanique des fluides, on dit qu'un fluide est en écoulement incompressible si la divergence du champ des vitesses vaut zéro.

Interprétation concernant le flux

La divergence peut être définie à partir du flux d'un champ de vecteur. Si ${\displaystyle D}$ est un domaine relativement compact de ${\displaystyle U}$, dont le bord est une surface lisse ${\displaystyle S}$, le flux de ${\displaystyle X}$ à travers ${\displaystyle S}$ est égal à l'intégrale sur ${\displaystyle D}$ de la divergence. Explicitement

${\displaystyle \int _{D}(\operatorname {div} X)\mathrm {d} x\mathrm {d} y\mathrm {d} z=\int _{S}i(X)(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)=\int _{S}g(X,\nu )\Omega _{S}}$

Dans la dernière intégrale, ${\displaystyle \nu }$ est le vecteur unitaire normal sortant de ${\displaystyle S}$, et ${\displaystyle \Omega _{S}}$ est l'élément d'aire de la surface ${\displaystyle S}$. Cette égalité est valable en toute dimension, et s'étend aux domaines à bord des variétés riemanniennes orientées^[2]. Elle est connue sous le nom de théorème de Green-Ostrogradski (en dimension 3) ou théorème de flux-divergence, qui est l'une des nombreuses variantes du théorème de Stokes

Démonstration

On écrit ${\displaystyle X=\langle X,\nu \rangle \nu +X^{T}}$, où le vecteur ${\displaystyle X^{T}}$ est tangent à la surface. On a alors

${\displaystyle i(X)(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)=\langle X,\nu \rangle (\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)}$

Mais d'une part, d'après la formule de Cartan

${\displaystyle i(X)(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)=L_{X}(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)=(\operatorname {div} X))(\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z)}$

D'autre part l'élément d'aire de S est donné par ${\displaystyle i(\nu )\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z}$. Le résultat s'en déduit par le théorème de Stokes.

Cette preuve s'étend telle que à la dimension n.

Divergence en dimension n

Cette définition et ses propriétés s'étendent aux champs de vecteurs sur ${\displaystyle \mathbb {R} ^{n}}$. Si ${\displaystyle A=(A_{x_{i}})_{1\leq i\leq n}}$ est un tel champ de vecteurs, on pose

${\displaystyle \mathrm {div} A=\sum _{i=1}^{n}{\frac {\partial A_{x_{i}}}{\partial x_{i}}}}$

Pour ${\displaystyle \omega =\mathrm {d} x_{1}\wedge \dots \mathrm {d} x_{n}}$, on a encore ${\displaystyle L_{A}\omega =(\mathrm {div} A)\omega }$, d'où son lien avec le principe de (non)conservation du volume n-dimensionnel.

Démonstration

En utilisant le fait que la dérivée de Lie est une dérivation, on voit que

${\displaystyle L_{A}\omega =L_{A}(\mathrm {d} x_{1})\wedge \mathrm {d} x_{2}\wedge \ldots \wedge \mathrm {d} x_{n}+\mathrm {d} x_{1}\wedge L_{A}(\mathrm {d} x_{2})\wedge \ldots \wedge \mathrm {d} x_{n}+\ldots +\mathrm {d} x_{1}\wedge \mathrm {d} x_{2}\ldots \wedge L_{A}(\mathrm {d} x_{n})}$

Par ailleurs

${\displaystyle L_{A}(\mathrm {d} x_{i})=\mathrm {d} (L_{A}x_{i})=\mathrm {d} A_{x_{i}}}$

Ainsi, dans chacun des n termes de l'expression ci-dessus de ${\displaystyle L_{A}\omega }$, on peut remplacer ${\displaystyle \mathrm {d} A_{x_{i}}}$ par ${\displaystyle {\frac {\partial A_{x_{i}}}{\partial x_{i}}}\mathrm {d} x_{i}}$

Exemple. Pour le champ linéaire donné par

${\displaystyle A_{x_{i}}=\sum _{j=1}^{n}a_{j}^{i}x_{j}}$

la divergence est la trace de la matrice ${\displaystyle (a_{j}^{i})_{1\leq i,j\leq n}}$.

Propriétés

Divergence d’un champ rotationnel :

$${\displaystyle \operatorname {div} {\bigl (}{\overrightarrow {\operatorname {rot} }}\;{\vec {A}}{\bigr )}=0}$$

Cette formule est particulière à la dimension 3. Elle signifie qu'un champ rotationnel est à divergence nulle. Inversement, si un champ de vecteurs ${\displaystyle {\vec {B}}}$ sur un ouvert étoilé de ${\displaystyle \mathbb {R} ^{3}}$ est à divergence nulle, il existe un champ ${\displaystyle {\vec {A}}}$ tel que

$${\displaystyle {\vec {B}}={\overrightarrow {\operatorname {rot} }}\;{\vec {A}}}$$

(on dit alors que ${\displaystyle {\vec {A}}}$ est un potentiel vecteur). Cette propriété, une fois convenablement interprétée en termes de formes différentielles, est une application directe du lemme de Poincaré.

Attention. Le champ newtonien ${\displaystyle {\tfrac {\vec {r}}{r^{3}}}}$ est à divergence nulle, mais il n'existe pas de champ de vecteurs ${\displaystyle {\vec {A}}}$ tel que ${\displaystyle {\overrightarrow {\operatorname {rot} }}\;{\vec {A}}={\tfrac {\vec {r}}{r^{3}}}}$. En effet, si tel était le cas, son flux à travers toute surface fermée serait nul, alors que son flux à travers les sphères centrées à l'origine vaut ${\displaystyle 4\pi }$. En fait, ce champ n'est défini que sur l'espace privé de l'origine, qui n'est pas un ouvert étoilé : le lemme de Poincaré ne s'applique pas.

Interprétation comme transposé du gradient :

$${\displaystyle \operatorname {div} (f{\vec {A}})=f\operatorname {div} ({\vec {A}})+\nabla f\cdot {\vec {A}}}$$

Cette formule, qui est une conséquence directe de la formule de Leibniz, permet de voir l'opérateur divergence comme le transposé (au signe près) de l'opérateur gradient. En effet, d'après le théorème de Stokes, l'intégrale sur ${\displaystyle \mathbb {R} ^{n}}$ de la divergence d'un champ de vecteurs nul en dehors d'une partie bornée est nulle. Par conséquent, si ${\displaystyle f}$ est une fonction lisse et ${\displaystyle {\vec {A}}}$ un champ de vecteurs, tous deux nuls en dehors d'une partie bornée (cette condition assurant que les intégrales ont un sens),

$${\displaystyle \int _{\mathbb {R} ^{n}}f\operatorname {div} {\vec {A}}\;\mathrm {d} x_{1}\ldots \mathrm {d} x_{n}=-\int _{\mathbb {R} ^{n}}\nabla f\cdot {\vec {A}}\;\mathrm {d} x_{1}\ldots \mathrm {d} x_{n}}$$

Cette propriété s'interprète de la façon suivante. Soient ${\displaystyle C^{\infty }(\mathbb {R} ^{n})}$ et ${\displaystyle \operatorname {Vect} (\mathbb {R} ^{n})}$ respectivement les espaces vectoriels des fonctions lisses et des champs de vecteurs sur ${\displaystyle \mathbb {R} ^{n}}$ à support compact. On les munit des produits scalaires

$${\displaystyle \langle f,g\rangle :=\int _{\mathbb {R} ^{n}}f\,g\;\mathrm {d} x_{1}\cdots \mathrm {d} x_{n}}$$

et

$${\displaystyle \langle {\vec {A}},{\vec {B}}\rangle :=\int _{\mathbb {R} ^{n}}{\vec {A}}\cdot {\vec {B}}\;\mathrm {d} x_{1}\cdots \mathrm {d} x_{n}}$$

Alors ${\displaystyle \langle \nabla f,{\vec {A}}\rangle =-\langle f,\operatorname {div} {\vec {A}}\rangle }$, ce qui prouve cette assertion.

Cette interprétation de la divergence présente l'avantage de se généraliser aussi bien aux variétés riemanniennes qu'aux tenseurs.

Divergence d’un produit vectoriel :

$${\displaystyle \operatorname {div} ({\vec {A}}\wedge {\vec {B}})={\vec {B}}\cdot \operatorname {rot} {\vec {A}}-{\vec {A}}\cdot \operatorname {rot} {\vec {B}}}$$

Une application typique de cette formule est le théorème de Poynting en électromagnétisme.

Relations avec d’autres opérateurs :

$${\displaystyle {\overrightarrow {\operatorname {rot} }}{\Bigl (}{\overrightarrow {\operatorname {rot} }}{\bigl (}{\vec {A}}{\bigr )}{\Bigr )}={\overrightarrow {\operatorname {grad} }}{\Bigl (}\operatorname {div} {\bigl (}{\vec {A}}{\bigr )}{\Bigr )}-\Delta {\bigl (}{\vec {A}}{\bigr )}}$$

Ces relations, très utilisées en analyse vectorielle, se comprennent mieux dans le cadre des formes différentielles.

Utilisation en physique

Lois de conservation

D'une manière générale, la divergence est reliée en physique à l'expression locale de la propriété de conservation d'une grandeur. En considérant une surface fermée quelconque ${\displaystyle (S)}$, la variation d'une grandeur conservative dans le volume fermé par cette surface est, par définition d'une grandeur conservative, due aux échanges avec l'extérieur (il n'existe pas de sources de création ou d'annihilation d'une grandeur conservative). Le bilan de cette grandeur entre deux instants s'écrit donc uniquement comme la somme du flux de cette grandeur à travers la surface fermée ${\displaystyle (S)}$ et de la variation temporelle de la grandeur à l'intérieur de la surface ${\displaystyle (S)}$. Si la grandeur est conservative, ce bilan est nul.

Par exemple, en électromagnétisme, si ${\displaystyle {\vec {J}}}$ est le vecteur densité volumique courant, ${\displaystyle \rho }$ la densité volumique de charge électrique et ${\displaystyle V}$ le volume intérieur à la surface ${\displaystyle (S)}$, la conservation de la charge s'écrit de façon intégrale :

${\displaystyle \iint _{(S)}{\vec {J}}\cdot {\vec {n}}\,\mathrm {d} S+{\frac {\mathrm {d} }{\mathrm {d} t}}\iiint _{V}\rho \,\mathrm {d} V=0}$

ou encore, pour une surface ${\displaystyle (S)}$ fixe :

${\displaystyle \iint _{(S)}{\vec {J}}\cdot {\vec {n}}\,\mathrm {d} S+\iiint _{V}{\frac {\partial \rho }{\partial t}}\,\mathrm {d} V=0}$

avec ${\displaystyle {\vec {n}}}$ est un vecteur unitaire normal en tout point à ${\displaystyle (S)}$.

La formule de Green-Ostrogradsky permet de réécrire l'équation précédente à la manière de la divergence :

${\displaystyle \iiint _{V}\operatorname {div} ({\vec {J}})\,\mathrm {d} V+\iiint _{V}{\frac {\partial \rho }{\partial t}}\,\mathrm {d} V=0}$

Ce qui mène immédiatement à la relation locale de conservation :

${\displaystyle \operatorname {div} ({\vec {J}})+{\frac {\partial \rho }{\partial t}}=0}$

Il est ainsi également possible d'exprimer localement, par exemple dans le cadre de la mécanique des fluides, si ${\displaystyle \rho }$ est la masse volumique en un point et ${\displaystyle {\vec {V}}}$ le champ des vecteurs vitesse :

${\displaystyle \operatorname {div} (\rho \,{\vec {V}})+{\frac {\partial \rho }{\partial t}}=0}$ (équation de continuité).

D'autres lois de conservation font intervenir la divergence de tenseurs d'ordre 2, comme la conservation de la quantité de mouvement en mécanique des fluides. En relativité générale, on montre aussi la nullité de la divergence du tenseur énergie-impulsion.

Champs radiaux en carré inverse de la distance

Lorsqu'une loi d'interaction radiale, due à des sources ponctuelles, varie comme le carré inverse de la distance il est possible d'établir que le flux du champ d'interaction à travers une surface fermée est toujours proportionnel à la quantité de sources présentes à l'intérieur de la surface fermée. Ce type de relation porte généralement en physique le nom de théorème de Gauss. Par exemple, dans le cas du champ électrostatique ${\displaystyle {\vec {E}}}$, dû aux charges électriques ${\displaystyle Q_{\text{int}}}$ présentes à l'intérieur de la surface fermée ${\displaystyle (S)}$ on a la forme intégrale du théorème de Gauss suivante :

${\displaystyle \iint _{(S)}{\vec {E}}\cdot {\vec {n}}\,\mathrm {d} S={\frac {Q_{\text{int}}}{\varepsilon _{0}}}}$

Grâce au théorème de flux-divergence il est possible d'exprimer une forme locale du théorème de Gauss. L'équation précédente se réécrit :

${\displaystyle \iiint _{V}\operatorname {div} {\vec {E}}\,\mathrm {d} V={\frac {Q_{\text{int}}}{\varepsilon _{0}}}=\iiint _{V}{\frac {\rho }{\varepsilon _{0}}}\,\mathrm {d} V}$

si ${\displaystyle V}$ est le volume délimité par ${\displaystyle (S)}$ et ${\displaystyle \rho }$ la densité volumique de charge. On obtient alors immédiatement :

${\displaystyle \operatorname {div} {\vec {E}}={\frac {\rho }{\varepsilon _{0}}}}$

qui est la forme locale du théorème de Gauss. Ce type de relation est également possible pour le champ de gravitation :

${\displaystyle \operatorname {div} {\vec {G}}=-4\pi \,G\,\rho }$

où ${\displaystyle G}$ est la constante fondamentale de la gravitation, ${\displaystyle {\vec {G}}}$ le champ de gravitation et ${\displaystyle \rho }$ la masse volumique.

Flux du champ magnétique

En électromagnétisme il est possible de montrer, à partir de la loi de Biot et Savart, que la divergence du champ magnétique ${\displaystyle {\vec {B}}}$ est nulle^[a] :

${\displaystyle \operatorname {div} {\vec {B}}=0}$

Cette propriété intrinsèque du champ magnétique permet d'établir que le flux du champ magnétique à travers une surface fermée est toujours nul ; on dit que le champ magnétique est à flux conservatif. En effet, si on appelle ${\displaystyle (S)}$ la surface fermée considérée et ${\displaystyle V}$ le volume intérieur à cette surface, on a :

${\displaystyle \iint _{(S)}{\vec {B}}\cdot {\vec {n}}\,\mathrm {d} S=\iiint _{V}\operatorname {div} ({\vec {B}})\,\mathrm {d} V=0}$

Expression de la divergence en dimension 3 dans d'autres systèmes de coordonnées

En coordonnées cylindriques

${\displaystyle (x,y,z)=(r\cos \theta ,r\sin \theta ,z),0\leq \theta <2\pi }$

$${\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {A}}={\frac {1}{r}}{\frac {\partial (rA_{r})}{\partial r}}+{\frac {1}{r}}{\frac {\partial A_{\theta }}{\partial \theta }}+{\frac {\partial A_{z}}{\partial z}}}$$

En coordonnées sphériques

En choisissant pour convention les notations physiques (conformément au standard ISO 31-11), soit ${\displaystyle (x,y,z)=(r\sin \theta \cos \varphi ,r\sin \theta \sin \varphi ,r\cos \theta ),0\leq \theta \leq \pi ,0\leq \varphi <2\pi }$ :

$${\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {A}}={\frac {1}{r^{2}}}{\frac {\partial (r^{2}A_{r})}{\partial r}}+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta A_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}}$$

Notes et références

Notes

Références

Voir aussi

Bibliographie

• (en) Yvonne Choquet-Bruhat et Cécile DeWitt-Morette, Analysis, Manifolds & Physics - Part I: Basics, North-Holland/Elsevier (2^e édition révisée - 1982) (ISBN 0-444-86017-7)
• Richard P. Feynman, Robert B. Leighton et Matthew Sands (en), Le Cours de physique de Feynman [détail de l’édition], Électromagnétisme I, ch. 2 et 3, InterEditions (ISBN 2-72960028-0)
• Jacques Lafontaine, Introduction aux variétés différentielles [détail des éditions]
• François Rouvière, Petit guide de calcul différentiel à l'usage de la licence et de l'agrégation, Cassini, 1999 (ISBN 2-84225-008-7)
• (en) Sylvestre Gallot, Dominique Hulin et Jacques Lafontaine, Riemannian Geometry [détail des éditions]

Articles connexes

• Divergence d'un tenseur
• Rotationnel, gradient, nabla, laplacien
• Dérivée partielle, équation aux dérivées partielles
• Opérateur différentiel
• Théorème de Stokes
• Équations de Maxwell, équations de Navier-Stokes

v · m Analyse vectorielle
Objets d'étude	Champ de vecteurs Champ scalaire Équation aux dérivées partielles Équation de Laplace Équation de Poisson
Opérateurs	Nabla Gradient Rotationnel Rotationnel du rotationnel Divergence Laplacien scalaire Bilaplacien Laplacien vectoriel D'alembertien Advection
Théorèmes	Théorème de Green Théorème de Stokes Théorème de Helmholtz-Hodge Théorème de la divergence Théorème du gradient Théorème du rotationnel

• Portail de l'analyse
• Portail de la physique