Distribuzione lognormale

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti.

Distribuzione lognormale
Funzione di densità di probabilità
Funzione di ripartizione
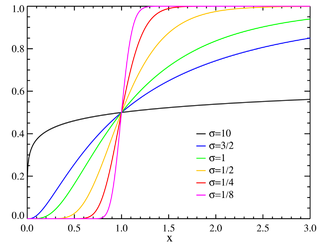Parametri	$\mu \in \mathbb {R}$ $\sigma ^{2}\in \mathbb {R} _{0}^{+}$
Supporto	$\mathbb {R} _{0}^{+}$
Funzione di densità	${\frac {e^{-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}}}{{\sqrt {2\pi }}{\sigma }x}}$
Funzione di ripartizione	${\frac {1}{2}}+{\frac {1}{2}}{\text{erf}}\left({\frac {\ln x-\mu }{{\sqrt {2}}\sigma }}\right)$
Valore atteso	$e^{\mu +{\frac {\sigma ^{2}}{2}}}$
Mediana	$e^{\mu }\$
Moda	$e^{\mu -\sigma ^{2}}$
Varianza	$e^{2\mu +\sigma ^{2}}(e^{\sigma ^{2}}-1)$
Indice di asimmetria	$(e^{\sigma ^{2}}+2){\sqrt {e^{\sigma ^{2}}-1}}$
Curtosi	$e^{4\sigma ^{2}}+2e^{3\sigma ^{2}}+3e^{2\sigma ^{2}}-6$
Entropia	${\frac {1}{2}}+\mu +{\frac {1}{2}}\log(2\pi \sigma ^{2})$
Manuale

In teoria delle probabilità la distribuzione lognormale, o log-normale, è la distribuzione di probabilità di una variabile aleatoria $X$ il cui logaritmo $\log X$ segue una distribuzione normale.

Questa distribuzione può approssimare il prodotto di molte variabili aleatorie positive indipendenti.

Viene utilizzata anche in matematica finanziaria.

Definizione

La variabile aleatoria $X=e^{N}$ segue la distribuzione lognormale $\log {\mathcal {X}}(\mu ,\sigma ^{2})$ se e solo se $N=\log X$ segue la distribuzione normale ${\mathcal {N}}(\mu ,\sigma ^{2})$ .

La sua funzione di densità di probabilità è

f(x)={\frac {e^{-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}}}{x{\sqrt {2\pi }}{\sigma }}}

per

x>0

Caratteristiche

La funzione di ripartizione della distribuzione lognormale è

F(x)=\Phi _{(\mu ,\sigma )}(\ln x)={\tfrac {1}{2}}+{\tfrac {1}{2}}{\text{erf}}\left({\frac {\ln x-\mu }{{\sqrt {2}}\sigma }}\right)

dove $\Phi _{(\mu ,\sigma )}$ è la funzione di ripartizione della distribuzione normale ed ${\text{erf}}$ è la funzione degli errori.

I momenti semplici della distribuzione possono essere dedotti dalla funzione generatrice dei momenti della distribuzione normale di $N=\log X$

\mu _{n}(X)=E[X^{n}]=E[e^{nN}]=g_{N}(n)=e^{n\mu +n^{2}{\frac {\sigma ^{2}}{2}}}

In particolare si trovano

la speranza matematica

E[X]=e^{\mu +{\frac {\sigma ^{2}}{2}}}

e la varianza

{\text{Var}}(X)=E[X^{2}]-E[X]^{2}=e^{2\mu }(e^{2\sigma ^{2}}-e^{\sigma ^{2}})=e^{2\mu +\sigma ^{2}}(e^{\sigma ^{2}}-1)

I parametri $(\mu ,\sigma ^{2})$ possono essere ricavati dalla speranza e dalla varianza, utilizzando la relazione ${\tfrac {{\text{Var}}(X)}{E[X]^{2}}}=e^{\sigma ^{2}}-1$ .

Gli indici di asimmetria e curtosi sono

\gamma _{1}=(e^{\sigma ^{2}}+2){\sqrt {e^{\sigma ^{2}}-1}}

\gamma _{2}=e^{4\sigma ^{2}}+2e^{3\sigma ^{2}}+3e^{2\sigma ^{2}}-6

La moda della distribuzione è $e^{\mu -\sigma ^{2}}$ .

La mediana è $q_{1/2}=e^{\mu }$ e si trova immediatamente tramite la mediana $\mu$ di $N=\log X$ : ${\tfrac {1}{2}}=P(N\leqslant \mu )=P(X=e^{N}\leqslant e^{\mu })$ .

Proprietà

Se $X$ è una variabile aleatoria con distribuzione lognormale $\log {\mathcal {N}}(e^{\mu +{\frac {1}{2}}\sigma ^{2}},e^{2\mu +\sigma ^{2}}(e^{\sigma ^{2}}-1))$ allora

$N=\log X$ segue la distribuzione normale ${\mathcal {N}}(\mu ,\sigma ^{2})$ .

Per ogni trasformazione lineare (invertibile)

$aN+b$ segue ancora una distribuzione normale ${\mathcal {N}}(a\mu +b,a^{2}\sigma ^{2})$
$e^{aN+b}=e^{b}X^{a}$ segue una distribuzione lognormale $\log {\mathcal {N}}(a\mu +b,a^{2}\sigma ^{2})$ .

In particolare seguono una distribuzione lognormale

i multipli scalari $cX$ ,
le potenze $X^{a}$
e l'inverso $X^{-1}$ di $X$ .

Per la definizione di distribuzione lognormale non è importante che venga scelto il logaritmo naturale, ovvero la base e: due distinti logaritmi $\log _{a}X$ e $\log _{b}X$ differiscono soltanto di un fattore ${\tfrac {\log a}{\log b}}$ .

La distribuzione lognormale svolge un ruolo simile a quello della distribuzione normale, la quale può fornire un'approssimazione per la somma di "molte" variabili aleatorie indipendenti $X_{1},...X_{n}$ aventi una stessa distribuzione (teorema del limite centrale). Se le $X_{i}$ sono positive allora la distribuzione lognormale può fornire un'approssimazione per il loro prodotto (così come la distribuzione normale può fornire un'approssimazione per la somma dei loro logaritmi, $\textstyle \log(\prod _{i}X_{i})=\sum _{i}\log(X_{i}$ ).