バターワースフィルタ (英 : Butterworth filter )は、フィルタ回路 設計の一種。通過帯域 が数学的に可能な限り平坦な周波数特性 となるよう設計されている。
バターワースフィルタは1930年 、イギリス の技術者 スティーブン・バターワース(英語版) が論文 "On the Theory of Filter Amplifiers" (Butterworth 1930 ) で発表した。
また、特定のフィルタ回路 構成を指す用語ではなく、フィルタの応答特性を指す用語であるため、バターワースフィルタ特性 (あるいはバターワース特性 )と呼ぶ場合もある。
概要 バターワースフィルタの周波数応答は通過帯域では最大限平坦であり(リップルがない)、除去帯域に向かってゼロに近づいていく。対数目盛のボーデ図 で見ると、応答曲線は線形に負の無限大に近づいていく。一次フィルタの場合、応答曲線の傾斜は -6dB /octave または -20dB/decade となる(回路構成に関わらず、一次のバターワースフィルタは全てこの特性を示す)。二次バターワースフィルタの場合、応答曲線の傾斜は -12dB/octave、三次の場合 -18dB/octave となる。バターワースフィルタは、ωに対して振幅が単調に変化する。バターワースフィルタは高次になっても特性曲線が同じ形状(ただし、傾斜はきつくなる)だが、他のフィルタ(ベッセル 、チェビシェフ 、楕円 など)は高次になると曲線の形状が変わる。
他のフィルタに比べるとバターワースフィルタによる減衰は緩やかであるため、特定の除去帯域仕様を実装するには高次な実装を必要とする。しかし、通過帯域は他のフィルタより線形な位相応答を示す。
簡単な例 三次ローパスフィルタ(Cauer形)。このフィルタが遮断周波数 ωc =1 のバターワースフィルタとなるのは、(例えば)C2 =4/3 F 、R4 =1 Ω 、L1 =3/2 H、L3 =1/2 H の場合である。 バターワースフィルタの簡単な例として三次ローパスフィルタ を右図に示す。 C 2 = 4 / 3 {\displaystyle C_{2}=4/3} F 、 R 4 = 1 {\displaystyle R_{4}=1} Ω 、 L 1 = 3 / 2 {\displaystyle L_{1}=3/2} L 3 = 1 / 2 {\displaystyle L_{3}=1/2} s = σ + j ω {\displaystyle s=\sigma +j\omega } C のインピーダンス を 1/Cs 、コイル L のインピーダンスを Ls としたとき、この回路の伝達関数 は以下のようになる。
H ( s ) = V o u t ( s ) V i n ( s ) = 1 1 + 2 s + 2 s 2 + s 3 {\displaystyle H(s)={\frac {V_{out}(s)}{V_{in}(s)}}={\frac {1}{1+2s+2s^{2}+s^{3}}}} 周波数応答の大きさ(利得) G ( ω ) {\displaystyle G(\omega )}
G 2 ( ω ) = | H ( j ω ) | 2 = 1 1 + ω 6 {\displaystyle G^{2}(\omega )=|H(j\omega )|^{2}={\frac {1}{1+\omega ^{6}}}\,}
また、位相 は以下の式で得られる。
Φ ( ω ) = arg ( H ( j ω ) ) {\displaystyle \Phi (\omega )=\arg(H(j\omega ))\,} ωc =1 の三次バターワースフィルタの利得(緑)と群遅延(赤) 群遅延 は、角周波数についての位相の微分と定義され、異なる複数の周波数間の位相差による信号の歪みの尺度である。このフィルタの利得と遅延をプロットしたものを左図に示す。利得曲線を見ると、通過帯域にも除去帯域にもリップルがないことがわかる。
伝達関数 H(s) の絶対値の対数を複素平面にプロットしたものが右図である。複素平面の左半分に3つの極がある。これらは単位円 上にあり、実数軸を中心として対称に位置する。利得関数は右半分に3つの極を持ち、全体として単位円が完成する。
この回路のコイルとコンデンサを入れ替えると、ハイパス ・バターワースフィルタとなる。うまく計算した値のコイルとコンデンサを並列接続したものをそれぞれの位置に入れると、バンドパス ・バターワースフィルタになる。
伝達関数 一次から五次までのバターワース特性のローパスフィルタの利得。n 次のとき、傾斜は 20n dB/decade になっている。 n 次バターワース・ローパス・フィルタの利得 G ( ω ) {\displaystyle G(\omega )} 伝達関数 H(s) から次のように得られる。
G 2 ( ω ) = | H ( j ω ) | 2 = G 0 2 1 + ( ω ω c ) 2 n {\displaystyle G^{2}(\omega )=\left|H(j\omega )\right|^{2}={\frac {G_{0}^{2}}{1+\left({\frac {\omega }{\omega _{c}}}\right)^{2n}}}} ここで
n はフィルタの次数 ωc は遮断周波数 (約 -3dB となる周波数) G 0 {\displaystyle G_{0}} である。
n が無限大に近づくと、利得は矩形関数 となり、ωc 以下の周波数は利得 G 0 {\displaystyle G_{0}} c 以上の周波数は抑止される。n が小さいほど、遮断は緩やかになる。
s = σ + j ω {\displaystyle s=\sigma +j\omega } H(s) を決定することを考える。s = jω のときの H(s)H(-s) を計算すると |H(jω) |2 と同じになるため、次が得られる。
H ( s ) H ( − s ) = G 0 2 1 + ( − s 2 ω c 2 ) n {\displaystyle H(s)H(-s)={\frac {G_{0}^{2}}{1+\left({\frac {-s^{2}}{\omega _{c}^{2}}}\right)^{n}}}} この式の極は半径 ωc の円上に等間隔で現れる。伝達関数自体は複素平面 s 上の実数が負の側の極で決定される。k 番目の極は次の式で決定される。
− s k 2 ω c 2 = ( − 1 ) 1 n = e j ( 2 k − 1 ) π n k = 1 , 2 , 3 , … , n {\displaystyle -{\frac {s_{k}^{2}}{\omega _{c}^{2}}}=(-1)^{\frac {1}{n}}=e^{\frac {j(2k-1)\pi }{n}}\qquad \mathrm {k=1,2,3,\ldots ,n} } 従って、次が得られる。
s k = ω c e j ( 2 k + n − 1 ) π 2 n k = 1 , 2 , 3 , … , n {\displaystyle s_{k}=\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}\qquad \mathrm {k=1,2,3,\ldots ,n} } 伝達関数はこれらの極を使って次のようにも表せる。
H ( s ) = G 0 ∏ k = 1 n ( s − s k ) / ω c {\displaystyle H(s)={\frac {G_{0}}{\prod _{k=1}^{n}(s-s_{k})/\omega _{c}}}} 分母は、s におけるバターワース多項式である。
正規化バターワース多項式 バターワース多項式は上記のように複素数形式でも書けるが、複素共役な極同士を掛け合わせることで実数形式で書くこともできる。この多項式は ω c = 1 {\displaystyle \omega _{c}=1}
B n ( s ) = ∏ k = 1 n 2 [ s 2 − 2 s cos ( 2 k + n − 1 2 n π ) + 1 ] {\displaystyle B_{n}(s)=\prod _{k=1}^{\frac {n}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]} B n ( s ) = ( s + 1 ) ∏ k = 1 n − 1 2 [ s 2 − 2 s cos ( 2 k + n − 1 2 n π ) + 1 ] {\displaystyle B_{n}(s)=(s+1)\prod _{k=1}^{\frac {n-1}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]} 小数点以下第4位まで表すと、以下のようになる。
n 多項式 Bn (s) 1 ( s + 1 ) {\displaystyle (s+1)} 2 s 2 + 1.4142 s + 1 {\displaystyle s^{2}+1.4142s+1} 3 ( s + 1 ) ( s 2 + s + 1 ) {\displaystyle (s+1)(s^{2}+s+1)} 4 ( s 2 + 0.7654 s + 1 ) ( s 2 + 1.8478 s + 1 ) {\displaystyle (s^{2}+0.7654s+1)(s^{2}+1.8478s+1)} 5 ( s + 1 ) ( s 2 + 0.6180 s + 1 ) ( s 2 + 1.6180 s + 1 ) {\displaystyle (s+1)(s^{2}+0.6180s+1)(s^{2}+1.6180s+1)} 6 ( s 2 + 0.5176 s + 1 ) ( s 2 + 1.4142 s + 1 ) ( s 2 + 1.9319 s + 1 ) {\displaystyle (s^{2}+0.5176s+1)(s^{2}+1.4142s+1)(s^{2}+1.9319s+1)} 7 ( s + 1 ) ( s 2 + 0.4450 s + 1 ) ( s 2 + 1.2470 s + 1 ) ( s 2 + 1.8019 s + 1 ) {\displaystyle (s+1)(s^{2}+0.4450s+1)(s^{2}+1.2470s+1)(s^{2}+1.8019s+1)} 8 ( s 2 + 0.3902 s + 1 ) ( s 2 + 1.1111 s + 1 ) ( s 2 + 1.6629 s + 1 ) ( s 2 + 1.9616 s + 1 ) {\displaystyle (s^{2}+0.3902s+1)(s^{2}+1.1111s+1)(s^{2}+1.6629s+1)(s^{2}+1.9616s+1)}
最大平坦性 ω c = 1 {\displaystyle \omega _{c}=1} G 0 = 1 {\displaystyle G_{0}=1}
d G d ω = − n G 3 ω 2 n − 1 {\displaystyle {\frac {dG}{d\omega }}=-nG^{3}\omega ^{2n-1}} 利得 G は常に正なので、全ての ω {\displaystyle \omega }
G ( ω ) = 1 − 1 2 ω 2 n + 3 8 ω 4 n + … {\displaystyle G(\omega )=1-{\frac {1}{2}}\omega ^{2n}+{\frac {3}{8}}\omega ^{4n}+\ldots } 言い換えれば、利得の導関数は2n 次導関数を超えるまでゼロであり、それにより最大平坦性を生じる。
高周波ロールオフ 再度 ω c = 1 {\displaystyle \omega _{c}=1}
lim ω → ∞ d log ( G ) d log ( ω ) = − n {\displaystyle \lim _{\omega \rightarrow \infty }{\frac {d\log(G)}{d\log(\omega )}}=-n} デシベル で表すと、高周波ロールオフは 20n dB/decade または 6n dB/octave となる(電力は電圧利得の二乗に比例するため、20 という係数が使われる)。
フィルタ設計 線形のアナログフィルタ回路の実装には、様々なトポロジーが存在する。あるトポロジーの回路は構成は同じだが、個々の部品の特性値が異なる。
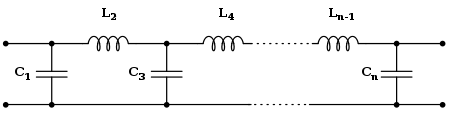
Cauer形 Cauer形のバターワースフィルタ Cauer形は受動部品だけで線形アナログフィルタを構成する。バターワースフィルタの伝達関数はCauer形の回路で実装できる。右図のk番目の部品の特性値は以下のようになる。
C k = 2 sin [ ( 2 k − 1 ) 2 n π ] {\displaystyle C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]} L k = 2 sin [ ( 2 k − 1 ) 2 n π ] {\displaystyle L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]} Sallen-Key形 Sallen-Key形(単にトポロジーを示しているだけで、個々の値はバターワースフィルタとは限らない) Sallen-Key形は能動部品(オペアンプ )も使って線形アナログフィルタを実装するトポロジーである。各段のSallen-Key形回路で複素共役の2つの極を実装する。全体としては、Sallen-Key形の回路をカスケード接続してフィルタを構成する。n が奇数の場合実数の極ができるが、それは別途実装する必要があり、一般にRC回路 で構成して、それをオペアンプの回路とカスケード接続する。
Sallen-Key形の伝達関数は次の通りである。
H ( s ) = 1 1 + C 2 ( R 1 + R 2 ) s + C 1 C 2 R 1 R 2 s 2 {\displaystyle H(s)={\frac {1}{1+C_{2}(R_{1}+R_{2})s+C_{1}C_{2}R_{1}R_{2}s^{2}}}} この分母がバターワース多項式の二次項の1つになるよう設定すればよい。 ω c = 1 {\displaystyle \omega _{c}=1}
C 1 C 2 R 1 R 2 = 1 {\displaystyle C_{1}C_{2}R_{1}R_{2}=1\,} かつ
C 2 ( R 1 + R 2 ) = 2 cos ( 2 k + n − 1 2 n π ) {\displaystyle C_{2}(R_{1}+R_{2})=2\cos \left({\frac {2k+n-1}{2n}}\pi \right)} となるように設定する。この場合、2つの部品の値が定まらないが、好きなように選べばよい。
デジタルでの実装 バターワースフィルタをデジタルフィルタとして実装する場合、双一次変換 やZ変換 を使ってアナログフィルタを離散化することが多い。高次の場合、量子化誤差 の影響が出やすくなる。そのためバイクアッド・フィルタ(英語版) をカスケード接続したものとして計算することが多い(奇数次の場合は、一次フィルタもカスケード接続する)。
他の線形フィルタとの比較 下図は、離散時間バターワースフィルタと他のフィルタの利得を示したものである。いずれも五次のフィルタである。
これらは同じ次数(この場合は五次)である。五次のフィルタであるとは、decade(周波数が10倍になる区間)当たり20dB×5 すなわち 100dB のロールオフとなることを意味する。バターワースフィルタは他のフィルタに比べて遮断周波数 付近でのロールオフが緩やかだが、リップルが見られない。
参考文献 Stephen Butterworth (1930). “On the Theory of Filter Amplifiers” (英語) (PDF). Experimental Wireless and the Radio Engineer 7 (85): 536-541. https://worldradiohistory.com/UK/Experimental-Wireless/30s/Wireless-Engineer-1930-10.pdf . 




















![{\displaystyle B_{n}(s)=\prod _{k=1}^{\frac {n}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187e9a2c6bc7c89f6130001674b6b6b352ed096f)
![{\displaystyle B_{n}(s)=(s+1)\prod _{k=1}^{\frac {n-1}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8353ee9b21666bab79a2a0e72a76c5c097a832aa)













![{\displaystyle C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68f23aa51ad46a68f0cb9d82e2ed3235ef9ee49b)
![{\displaystyle L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b083cc1dc88cd5443bc52baf7f229d1123322de7)











