Herons formel

Herons formel er i euklidsk geometri en formel for sammenhengen mellom arealet av en trekant og lengden av de tre trekantsidene. Formelen er oppkalt etter den greske matematikeren og ingeniøren Heron av Alexandria, som levde i hundreåret etter Kristi fødsel.

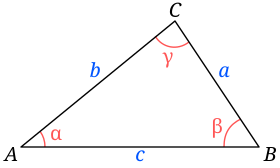
La lengden av de tre trekantsidene være definert som a, b og c. Herons formel sier da at arealet A til trekanten er gitt som

${\displaystyle A={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}}$

Her er s lik halve omkretsen til trekanten, det vil si

${\displaystyle s={\frac {1}{2}}(a+b+c)}$

Sannsynligvis var formelen allerede kjent på Herons tid, og mange mener at den stammer fra Arkimedes.

Herons formel er et spesielt tilfelle av Brahmaguptas formel for en syklisk firkant hvor en av sidene blir forsvinnende liten.

Bevis

Formelen kan bevises på flere forskjellige måter. Arealet til trekanten er alltid gitt ved det halve produktet av en side i trekanten multiplisert med høyden på denne siden. Velger man denne siden å være c, er da den tilsvarende høyden h = b sinα hvor vinkelen α er angitt i figuren. Den kan beregnes fra cosinussetningen som gir

${\displaystyle \cos \alpha ={b^{2}+c^{2}-a^{2} \over 2bc}}$

Ved bruk av trigonometri følger da at

${\displaystyle {\begin{aligned}A&={1 \over 2}bc\sin \alpha ={1 \over 2}bc\,{\sqrt {1-\cos ^{2}\alpha }}={1 \over 2}bc{\sqrt {1-\cos \alpha }}{\sqrt {1+\cos \alpha }}\\&={1 \over 2}bc{\sqrt {1-{b^{2}+c^{2}-a^{2} \over 2bc}}}{\sqrt {1+{b^{2}+c^{2}-a^{2} \over 2bc}}}={1 \over 4}{\sqrt {(a^{2}-(b-c)^{2})((b+c)^{2}-a^{2})}}\\&={1 \over 4}{\sqrt {(a+b-c)(a+c-b)(b+c+a)(b+c-a)}}\end{aligned}}}$

Her er summen a + b + c = 2s lik omkretsen til trekanten og Herons formel følger. Den behandler alle sidene likt og er derfor symmetrisk ved ombytte av disse.

Litteratur

• C.B. Boyer, A History of Mathematics, Princeton University Press, New Jersey (1985). ISBN 0-691-02391-3.