Distribuição triangular

Em probabilidade e estatística, a distribuição triangular é a distribuição de probabilidade contínua que possui um valor mínimo a, um valor máximo b e uma moda c, de modo que a função densidade de probabilidade é zero para os extremos (a e b), e afim entre cada extremo e a moda, de forma que o gráfico dela é um triângulo.

A distribuição triangular é uma distribuição muito simples e útil quando se tem poucos dados, conhecendo-se um valor mínimo (a), um valor máximo (b) e um valor mais provável (c) é possível obter uma distribuição triangular que resulta em uma boa aproximação das probabilidades de ocorrência do evento X.

Densidade

A função densidade de probabilidade é:

f ( x | a , b , c ) = { 2 ( x − a ) ( b − a ) ( c − a ) for  a ≤ x < c 2 b − a for  x = c 2 ( b − x ) ( b − a ) ( b − c ) for  c < x ≤ b 0 for any other case {\displaystyle f(x|a,b,c)={\begin{cases}{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c\\&\\{\frac {2}{b-a}}&{\text{for }}x=c\\&\\{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c<x\leq b\\&\\0&{\text{for any other case}}\end{cases}}}

Características da distribuição

Gráfico da função densidade|

Gráfico da probabilidade acumulada|

  • Parâmetros: a : a ∈ ( − ∞ , ∞ ) {\displaystyle a\colon a\in (-\infty ,\infty )}
    b : b > a {\displaystyle b\colon b>a}
    c : a ≤ c ≤ b {\displaystyle c\colon a\leq c\leq b}
  • Suporte: a ≤ x ≤ b {\displaystyle a\leq x\leq b}
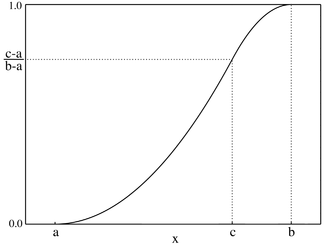
  • Função de probabilidade acumulada: = { ( x − a ) 2 ( b − a ) ( c − a ) for  a ≤ x < c c − a b − a for  x = c 1 − ( b − x ) 2 ( b − a ) ( b − c ) for  c < x ≤ b {\displaystyle {\begin{cases}{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{for }}a\leq x<c\\&\\{\frac {c-a}{b-a}}&{\text{for }}x=c\\&\\1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{for }}c<x\leq b\end{cases}}} Um exemplo prático da aplicação da distribuição uniforme pode ser conforme segue abaixo: Digamos que uma determinada empresa precise fazer um investimento, por qualquer que seja o motivo a empresa não conhece exatamente o montante desse investimento, mas conhece o valor mais provável e também os valores mínimo e máximo. Ela estima um valor mais provável para esse investimento em R$2.000.000,00, e estima que o valor mínimo que esse investimento pode assumir é 80% do valor mais provável e que o valor máximo que esse investimento pode assumir é 105% do valor mais provável. Nesse caso temos: c=2.000.000 a=1.600.000 b=2.100.000 Qual seria a probabilidade desse investimento ser de até R$1.800.000,00 ?

F ( x < 1.800.000 ) = ( ( 1.800.000 − 1.600.000 ) 2 ) / ( 2.100.000 − 1.600.000 ) ∗ ( 2.000.000 − 1.600.000 ) {\displaystyle F(x<1.800.000)=((1.800.000-1.600.000)^{2})/(2.100.000-1.600.000)*(2.000.000-1.600.000)}

F ( x < 1.800.000 ) = 0 , 2 {\displaystyle F(x<1.800.000)=0,2}

F ( x < 1.800.000 ) = 20 % {\displaystyle F(x<1.800.000)=20\%}

Média: a + b + c 3 {\displaystyle {\frac {a+b+c}{3}}}

  • Mediana: { a + ( b − a ) ( c − a ) 2 for  c ≥ b + a 2 b − ( b − a ) ( b − c ) 2 for  c ≤ b + a 2 {\displaystyle {\begin{cases}a+{\frac {\sqrt {(b-a)(c-a)}}{\sqrt {2}}}&{\text{for }}c\!\geq \!{\frac {b\!+\!a}{2}}\\&\\b-{\frac {\sqrt {(b-a)(b-c)}}{\sqrt {2}}}&{\text{for }}c\!\leq \!{\frac {b\!+\!a}{2}}\end{cases}}}
  • Moda: c {\displaystyle c\,}
  • Variância: a 2 + b 2 + c 2 − a b − a c − b c 18 {\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}
  • Obliquidade: 2 ( a + b − 2 c ) ( 2 a − b − c ) ( a − 2 b + c ) 5 ( a 2 + b 2 + c 2 − a b − a c − b c ) 3 2 {\displaystyle {\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}}
  • Curtose: − 3 5 {\displaystyle -{\frac {3}{5}}}
  • Entropia: 1 2 + ln ⁡ ( b − a 2 ) {\displaystyle {\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)}
  • Função geradora de momentos: 2 ( b − c ) e a t − ( b − a ) e c t + ( c − a ) e b t ( b − a ) ( c − a ) ( b − c ) t 2 {\displaystyle 2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}}
  • Função característica: − 2 ( b − c ) e i a t − ( b − a ) e i c t + ( c − a ) e i b t ( b − a ) ( c − a ) ( b − c ) t 2 {\displaystyle -2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}}


Uso da distribuição

A Distribuição Triangular é normalmente usada quando existe uma ideia subjetiva da população, através dos seus extremos e da sua moda.


Ligações externas

  • Weisstein, Eric W. «Triangular Distribution» (em inglês). MathWorld 
  • «Triangle Distribution» (PDF). , decisionsciences.org 
  • «Triangular Distribution». , brighton-webs.co.uk