Đồ thị hai phía đầy đủ

Trong lý thuyết đồ thị, một đồ thị hai phía đầy đủ (tiếng Anh: Complete bipartite graph hoặc biclique) là một dạng đồ thị hai phía đặc biệt, trong đó mỗi đỉnh của tập thứ nhất nối với mọi đỉnh thuộc tập thứ hai và ngược lại.^[1]

Định nghĩa

Cho ${\displaystyle G=(X,E)}$ là một đồ thị vô hướng lưỡng phân với hai tập ${\displaystyle X_{1}}$ và ${\displaystyle X_{2}}$ phân hoạch ${\displaystyle X}$ (${\displaystyle X_{1}}$ ${\displaystyle \neq }$ Ø ${\displaystyle \neq }$ ${\displaystyle X_{2}}$ và ${\displaystyle X_{1}}$ ${\displaystyle \bigcap }$ ${\displaystyle X_{2}}$ = Ø). Khi đó ${\displaystyle G}$ được gọi là lưỡng phân đầy đủ nếu:

     * Với mọi cặp đỉnh(i,j) mà i ${\displaystyle \in }$ ${\displaystyle X_{1}}$ và j ${\displaystyle \in }$ ${\displaystyle X_{2}}$ thì có đúng một cạnh của G nối i và j.

• Mối tương quan giữa đồ thị đầy đủ và đồ thị hai phía đầy đủ:^[2]

     * Đồ thị đầy đủ ${\displaystyle K_{n}}$ có: n đỉnh, ${\displaystyle {\cfrac {n.(n-1)}{2}}}$ cạnh
     * Đồ thị hai phía đầy đủ ${\displaystyle K_{m,n}}$ có: m + n đỉnh, m.n cạnh

Ví dụ

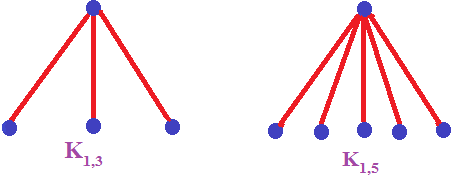
• Với mọi k, ${\displaystyle K_{1,k}}$ ta có đồ thị hình sao.^[3]

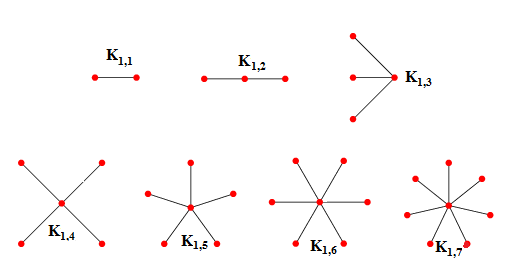
• Hay với đồ thị ${\displaystyle K_{1,k}}$ ta có đồ thị hình vuốt, hoặc một cây

• ${\displaystyle K_{m,n}}$ với m khác n.

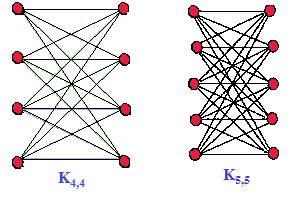
• ${\displaystyle K_{m,n}}$ với m = n.

Tính chất

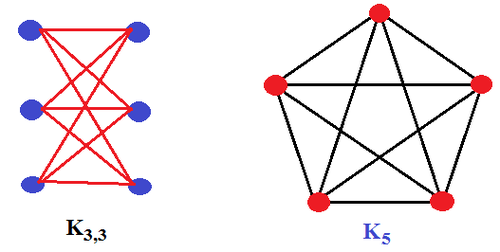
• Định lý Kuratowski ^[4][5] liên quan giữa tính phẳng của đồ thị và ${\displaystyle K_{3,3}}$: Điều kiện cần và đủ một đồ thị liên thông G có tính phẳng là G không chứa bất kỳ đồ thị con nào đồng phôi với ${\displaystyle K_{5}}$ hay ${\displaystyle K_{3,3}}$. Đồ thị ${\displaystyle K_{3,3}}$ là đồ thị không phẳng có ít cạnh nhất.

• Một đồ thị hai phía đầy đủ ${\displaystyle K_{m,n}}$ có số phủ đỉnh (Vertex covering number) bằng ${\displaystyle \min \lbrace m,n\rbrace }$ và số phủ cạnh (Edge covering number) bằng ${\displaystyle \max \lbrace m,n\rbrace }$
• Đồ thị hai phía đầy đủ ${\displaystyle K_{4,4}}$ là một Cayley Graph.^[6]
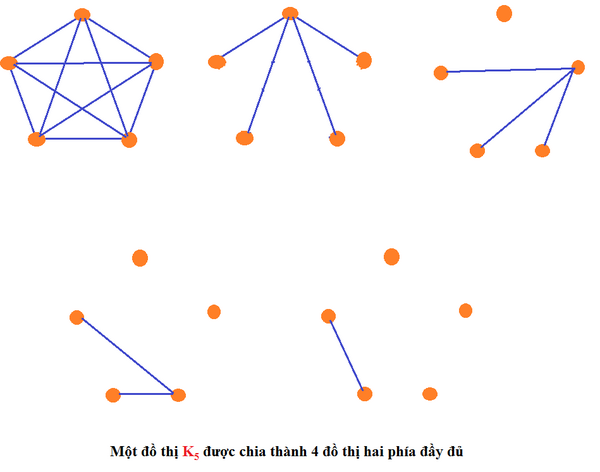
• Một đồ thị đủ ${\displaystyle K_{n}}$ có thể được tách thành 4 đồ thị con, mỗi đồ thị con là một đồ thị hai phía đầy đủ, ${\displaystyle H_{1}}$, ${\displaystyle H_{2}}$, ${\displaystyle H_{3}}$,... ${\displaystyle H_{m}}$, sao cho ${\displaystyle m\geq \;n-1}$^[7]

• Đồ thị hai phía đầy đủ ${\displaystyle K_{m,n}}$ là k-choosable khi và chỉ khi ${\displaystyle n<\;m^{m}}$ ^[8]

• Một đồ thị hai phía đầy đủ ${\displaystyle K_{m,n}}$ có cặp ghép hoàn hảo (Perfect matching) kích thước ${\displaystyle \min \lbrace m,n\rbrace }$
• Một đồ thị hai phía đầy đủ ${\displaystyle K_{n,n}}$ hay ${\displaystyle K_{n,n+1}}$ là một đồ thị Turán.^[9]
• Một đồ thị hai phía đầy đủ ${\displaystyle K_{m,n}}$ có mⁿ⁻¹ n^m−1 cây bao trùm
• Ma trận Laplace của đồ thị hai phía đầy đủ ${\displaystyle K_{m,n}}$ có các vectơ n+m, n, m, 0; với các vectơ tương thích 1, m-1, n-1, 1.
• Một đồ thị hai phía đầy đủ ${\displaystyle K_{n,n}}$ có một cách tô màu cạnh (Edge coloring) đúng đắn, n_Edge = n_color.^[10]

• Sắc số của đồ thị ${\displaystyle K_{m,n}}$ là 2 ^[11].
• Số màu cần thiết để tô màu các cạnh của ${\displaystyle K_{m,n}}$ là max{m.n} để không có 2 cạnh nào cùng màu mà lại có chung đỉnh.
• Đường kính của đồ thị hai phía đầy đủ: ${\displaystyle K_{1,1}}$ là 1, còn tất cả các ${\displaystyle K_{m,n}}$ khác đều có đường kính là 2.^[12]

Xem thêm

• Đồ thị hai phía
• Đồ thị chu trình
• Đồ thị đầy đủ
• Ma trận kề

Tham khảo