Carothers-Gleichung

Die Carothers-Gleichung beschreibt den Zusammenhang von Polymerisationsgrad ${\displaystyle \textstyle {\overline {X}}_{n}}$ und dem Umsatzgrad ${\displaystyle p}$ bei einer Stufenwachstumsreaktion. Sie ist nach Wallace Hume Carothers benannt.^[1] Es gibt mehrere Varianten, für lineare A–B-Systeme, lineare A–A/B–B-Systeme und nichtlineare Stufenwachstumsreaktionen. Bei linearen A–B-Systemen liegt ein Monomer vor, bei denen das Monomer zwei funktionellen Gruppen trägt, wie z. B. bei HO–R–COOH. Bei linearen A–A/B–B-Systemen liegen 2 Monomere vor, die jeweils eine der funktionellen Gruppen an beiden Ende tragen, wie z. B. bei HOOC–Ph–COOH und HO–(CH₂)₂–OH, die zu Polyethylenterephthalat reagieren können. Bei nichtlinearen Systemen liegen z. B. neben A–B-Monomeren auch trifunktionelle Monomere vor, was zur Vernetzung des Produkts führt.

Lineare Stufenwachstumsreaktionen

A-B-Systeme

Wenn ${\displaystyle N_{0}}$ die Zahl der ursprünglich vorhandenen Monomere und ${\displaystyle N_{t}}$ die Zahl der zum Zeitpunkt ${\displaystyle t}$ noch vorhandenen Moleküle ist (${\displaystyle N_{t}}$ umfasst alle Polymerisationsgrade: Monomere, Oligomere und Polymere), erhält man für den Umsatz ${\displaystyle p}$

${\displaystyle p={\frac {N_{0}-N_{t}}{N_{0}}}}$  (1)

p kann gleichzeitig auch als die Wahrscheinlichkeit, dass eine der Gruppen reagiert hat, betrachtet werden. Bei einem Umsatz von ${\displaystyle p=0{,}5}$ liegt die Wahrscheinlichkeit, dass eine Gruppe reagiert hat bei 50 %.

Den Polymerisationsgrad – die durchschnittliche Länge der Ketten – ${\displaystyle {\overline {X}}_{n}}$ kann man als den Bruch aus der Zahl der anfänglich vorhandenen Monomere durch die zur Zeit ${\displaystyle t}$ noch vorhandenen Moleküle ausdrücken:

${\displaystyle {\overline {X}}_{n}={\frac {N_{0}}{N_{t}}}}$   (2)

Durch Umformen von Gl. 1

${\displaystyle p={\frac {N_{0}-N_{t}}{N_{0}}}\Leftrightarrow {\frac {N_{0}}{N_{t}}}={\frac {1}{1-p}}}$

und einsetzen in Gl. 2 erhält man die Carothers-Gleichung für A-B-Systeme

${\displaystyle {\overline {X}}_{n}={\frac {1}{1-p}}}$

A-A/B-B-Systeme

Für A-A/B-B-Systeme muss man zusätzlich beachten, dass das System nicht stöchiometrisch zusammengesetzt sein kann, d. h. abweichende Monomerenverhältnis auftreten können. Darum definiert man einen Parameter ${\displaystyle r}$:

${\displaystyle r={\frac {N_{A}}{N_{B}}}}$

Der Parameter wird immer so definiert, dass ${\displaystyle r<1}$ ist, also mehr B-B im System vorliegt als A-A.

Damit erhält man als ${\displaystyle N_{0}}$

${\displaystyle N_{0}=N_{A}+N_{B}=rN_{B}+N_{B}}$

Zum Zeitpunkt ${\displaystyle t}$ sind beim Umsatz ${\displaystyle p_{A}}$ bereits ${\displaystyle pN_{A}}$ Moleküle der Sorte A-A umgesetzt. Für ${\displaystyle N_{t}}$, der Summe aus umgesetztem A-A und B-B gilt demnach ${\displaystyle 2pN_{A}=2rpN_{B}}$.

Die Menge an nicht umgesetzten Monomeren ${\displaystyle N_{t}}$ ist demnach

${\displaystyle N_{T}=N_{0}-2rpN_{B}=rN_{B}+N_{B}-2rpN_{B}}$

Auf dem Weg wie oben erhält man durch Einsetzen folgenden Ausdruck für ${\displaystyle {\overline {X}}_{n}}$

${\displaystyle {\overline {X}}_{n}={\frac {N_{0}}{N_{t}}}={\frac {rN_{B}+N_{B}}{rN_{B}+N_{B}-2rpN_{B}}}\Leftrightarrow }$

${\displaystyle {\overline {X}}_{n}={\frac {1+r}{1+r-2pr}}}$

was der Carothers-Gleichung für A-A/B-B-Systeme entspricht

Nichtlineare Stufenwachstumsreaktionen

A-B-Systeme

Setzt man den Monomeren trifunktionelle Monomere zu, kommt es zu einer Netzwerkbildung.

Um den Polymerisationsgrad berechnen zu können, definiert man eine durchschnittliche Funktionalität der Monomere

${\displaystyle f={\frac {\sum {N_{i}f_{i}}}{\sum {N_{i}}}}}$

Dabei ist ${\displaystyle f_{i}}$ die Zahl der funktionellen Gruppen am Molekül i und ${\displaystyle N_{i}}$ die Zahl der Monomermoleküle.

Bei ${\displaystyle N_{0}}$ Monomermoleküle sind insgesamt ${\displaystyle N_{0}\cdot f}$ funktionelle Gruppen vorhanden.

Nach einer Zeit ${\displaystyle t}$ haben ${\displaystyle 2(N_{0}-N_{t})}$ Gruppen reagiert, da für eine Bindung 2 Endgruppen reagieren müssen. Dadurch haben sich ${\displaystyle (N_{0}-N_{t})}$ Moleküle gebildet. Die Wahrscheinlichkeit einer Reaktion liegt also bei

${\displaystyle p={\frac {2(N_{0}-N_{t})}{fN_{0}}}}$   (3)

Umformen von Gl. 3 ergibt

${\displaystyle 2N_{t}=N_{0}(2-fp)}$

und nach Einsetzen in Gl. 2 erhält man eine Carothers-Gleichung für nichtlineare Systeme

${\displaystyle {\overline {X}}_{n}={\frac {2}{(2-pf)}}}$

Gleichung 3 lässt sich des Weiteren Umformen zu

${\displaystyle p={\frac {2}{f}}-{\frac {2}{f{\overline {X}}_{n}}}}$   (4)

Wenn der Polymerisationsgrad gegen unendlich geht, tritt Gelierung auf und in Gl. 4 geht der Ausdruck

${\displaystyle {\frac {2}{f{\overline {X}}_{n}}}\rightarrow 0}$

Damit gilt für den Umsatz ${\displaystyle p_{G}}$, wo das Gemisch anfängt zu gelieren:

${\displaystyle p_{G}={\frac {2}{f}}}$

Aus dieser Beziehung kann man erkennen, das schon bei deutlich geringeren Umsätzen als in den anderen Fällen ein hoher Polymerisationsgrad erreicht werden kann.

Diese Gleichung gilt nur für den Fall, dass das Gemisch stöchiometrisch (gleiche Anzahl von A wie B-Gruppen) zusammengesetzt ist.

Graphische Darstellung von Umsatz und Polymerisationsgrad

Die Bedeutung der Carothers-Gleichung kann man erkennen, wenn man den Polymerisationsgrad ${\displaystyle {\overline {X}}_{n}}$ gegen den Umsatz ${\displaystyle p}$ aufträgt:

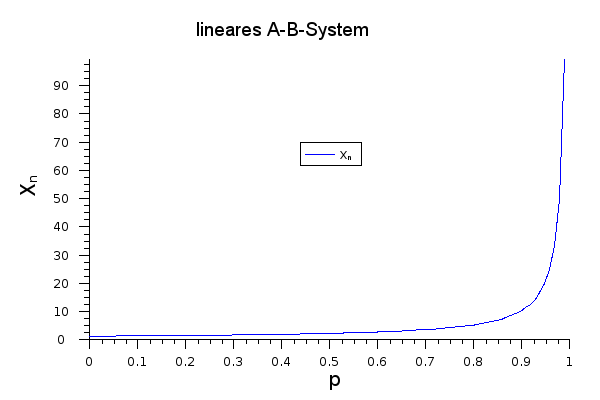
Erst bei sehr hohen Umsätzen erreicht der Polymerisationsgrad nennenswert große Werte. So beträgt er bei ${\displaystyle p=0{,}5}$ gerade einmal 2, einen Wert von 10.000 erreicht man erst bei einem Umsatzgrad von ${\displaystyle p=0{,}9999}$.

Genauso hat ${\displaystyle r}$ einen wesentlichen Einfluss auf den Polymerisationsgrad:

Schon kleine Abweichungen von ${\displaystyle r}$ vom Idealwert 1 bedeuten einen deutlich niedrigeren Polymerisationsgrad.

Bei Zugabe von Vernetzern steigt ${\displaystyle {\overline {X}}_{n}}$ hingegen schon bei niedrigerem Umsatz stark an:

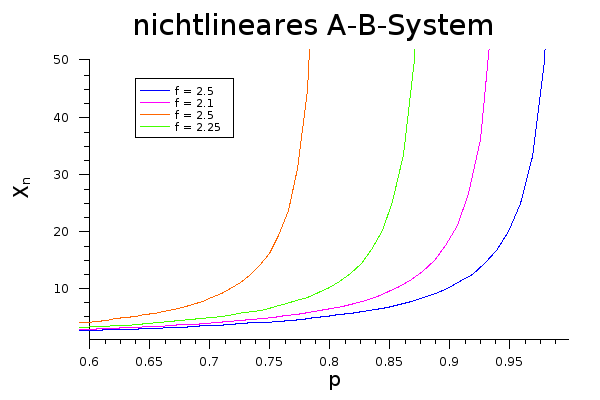
Einzelnachweise

1. ↑ Polymers: Chemistry and Physics of Modern Material, von John McKenzie, Grant Cowie. books.google.de, abgerufen am 23. Mai 2009. 

Weblinks

• Makromoleküle bei TU Chemnitz, Seite 25 (PDF-Datei; 505 kB)