Orthonormalbasis

Eine Orthonormalbasis (ONB) oder ein vollständiges Orthonormalsystem (VONS) ist in den mathematischen Gebieten lineare Algebra und Funktionalanalysis eine Menge von Vektoren aus einem Vektorraum mit Skalarprodukt (Innenproduktraum), welche auf die Länge eins normiert und zueinander orthogonal (daher Ortho-normal-basis) sind und deren lineare Hülle dicht im Vektorraum liegt. Im endlichdimensionalen Fall ist dies eine Basis des Vektorraums. Im unendlichdimensionalen Fall handelt es sich nicht um eine Vektorraumbasis im Sinn der linearen Algebra.

Verzichtet man auf die Bedingung, dass die Vektoren auf die Länge eins normiert sind, so spricht man von einer Orthogonalbasis.

Der Begriff der Orthonormalbasis ist sowohl im Fall endlicher Dimension als auch für unendlichdimensionale Räume, insbesondere Hilberträume, von großer Bedeutung.

Endlichdimensionale Räume

Im Folgenden sei ${\displaystyle V}$ ein endlichdimensionaler Innenproduktraum, das heißt, ein Vektorraum über ${\displaystyle \mathbb {R} }$ oder ${\displaystyle \mathbb {C} }$ mit Skalarprodukt ${\displaystyle \langle {\cdot },{\cdot }\rangle }$. Im komplexen Fall wird dabei vorausgesetzt, dass das Skalarprodukt linear im zweiten Argument und semilinear im ersten ist, also

${\displaystyle \lambda \langle v,w\rangle =\langle {\bar {\lambda }}v,w\rangle =\langle v,\lambda w\rangle }$

für alle Vektoren ${\displaystyle v,w\in V}$ und alle ${\displaystyle \lambda \in \mathbb {C} }$. Mit ${\displaystyle \|{\cdot }\|={\sqrt {\langle {\cdot },{\cdot }\rangle }}}$ wird die durch das Skalarprodukt induzierte Norm bezeichnet.

Definition und Existenz

Unter einer Orthonormalbasis eines ${\displaystyle n}$-dimensionalen Innenproduktraums ${\displaystyle V}$ versteht man eine Basis ${\displaystyle B=\{b_{1},\ldots ,b_{n}\}}$ von ${\displaystyle V}$, die ein Orthonormalsystem ist, das heißt:

• Jeder Basisvektor hat die Norm eins:

  ${\displaystyle \|b_{i}\|={\sqrt {\langle b_{i},b_{i}\rangle }}=1}$ für alle ${\displaystyle i\in \{1,\ldots ,n\}}$.

• Die Basisvektoren sind paarweise orthogonal:

  ${\displaystyle \langle b_{i},b_{j}\rangle =0}$ für alle ${\displaystyle i,j\in \{1,\ldots ,n\}}$ mit ${\displaystyle i\neq j}$.

Jeder endlichdimensionale Vektorraum mit Skalarprodukt besitzt eine Orthonormalbasis. Mit Hilfe des Gram-Schmidtschen Orthonormalisierungsverfahrens lässt sich aus jeder Basis eine Orthonormalbasis erzeugen.

Da Orthonormalsysteme stets linear unabhängig sind, bildet in einem ${\displaystyle n}$-dimensionalen Innenproduktraum ein Orthonormalsystem aus ${\displaystyle n}$ Vektoren bereits eine Orthonormalbasis.

Händigkeit der Basis

Gegeben sei eine geordnete Orthonormalbasis ${\displaystyle B=({b}_{1},\ldots ,{b}_{n})}$ von ${\displaystyle V}$. Dann ist die Matrix

${\displaystyle Q={\begin{pmatrix}{b}_{1}&{b}_{2}&\ldots &{b}_{n}\end{pmatrix}}}$

gebildet aus den als Spaltenvektoren notierten Vektoren ${\displaystyle {b}_{i}}$ orthogonal. Im Fall reeller Vektorräume muss dann die Determinante +1 oder −1 sein. Falls ${\displaystyle \operatorname {det} (Q)=+1}$ bilden die Vektoren ${\displaystyle {b}_{1},\ldots ,{b}_{n}}$ ein Rechtssystem.

Beispiele

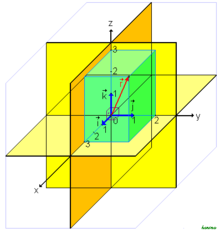
Beispiel 1

Die Standardbasis des ${\displaystyle \mathbb {R} ^{3}}$, bestehend aus den Vektoren

${\displaystyle {\vec {i}}={\vec {e}}_{1}={\begin{pmatrix}1\\0\\0\end{pmatrix}},\ {\vec {j}}={\vec {e}}_{2}={\begin{pmatrix}0\\1\\0\end{pmatrix}},\ {\vec {k}}={\vec {e}}_{3}={\begin{pmatrix}0\\0\\1\end{pmatrix}},}$

ist eine Orthonormalbasis des dreidimensionalen euklidischen Vektorraums ${\displaystyle \mathbb {R} ^{3}}$ (ausgestattet mit dem Standardskalarprodukt): Sie ist eine Basis des ${\displaystyle \mathbb {R} ^{3}}$, jeder dieser Vektoren hat die Länge 1, und je zwei dieser Vektoren stehen senkrecht aufeinander, denn ihr Skalarprodukt ist 0.

Allgemeiner ist im Koordinatenraum ${\displaystyle \mathbb {R} ^{n}}$ bzw. ${\displaystyle \mathbb {C} ^{n}}$, versehen mit dem Standardskalarprodukt, die Standardbasis ${\displaystyle \{e_{1},\dots ,e_{n}\}}$ eine Orthonormalbasis.

Beispiel 2

Die zwei Vektoren

${\displaystyle {\vec {b}}_{1}={\begin{pmatrix}{\tfrac {3}{5}}\\[1ex]{\tfrac {4}{5}}\end{pmatrix}}}$   und   ${\displaystyle {\vec {b}}_{2}={\begin{pmatrix}-{\tfrac {4}{5}}\\[1ex]{\tfrac {3}{5}}\end{pmatrix}}}$

bilden in ${\displaystyle \mathbb {R} ^{2}}$ mit dem Standardskalarprodukt ein Orthonormalsystem und daher auch eine Orthonormalbasis von ${\displaystyle \mathbb {R} ^{2}}$.

Koordinatendarstellung bezüglich einer Orthonormalbasis

Vektoren

Ist ${\displaystyle B=\{b_{1},\dots ,b_{n}\}}$ eine Orthonormalbasis von ${\displaystyle V}$, so lassen sich die Komponenten eines Vektors ${\displaystyle v\in V}$ bezüglich dieser Basis besonders leicht als Orthogonalprojektionen berechnen. Hat ${\displaystyle v}$ bezüglich der Basis ${\displaystyle B}$ die Darstellung

${\displaystyle v=v_{1}b_{1}+\dots +v_{n}b_{n}=\sum _{i=1}^{n}v_{i}b_{i},}$

so gilt

${\displaystyle v_{i}=\langle b_{i},v\rangle }$ für ${\displaystyle i=1,\dots ,n}$

denn

${\displaystyle \langle b_{i},v\rangle =\left\langle b_{i},\sum _{j=1}^{n}b_{j}v_{j}\right\rangle =\sum _{j=1}^{n}\left\langle b_{i},b_{j}v_{j}\right\rangle =\sum _{j=1}^{n}\left\langle b_{i},b_{j}\right\rangle v_{j}=\sum _{j=1 \atop j\neq i}^{n}\underbrace {\left\langle b_{i},b_{j}\right\rangle } _{0}v_{j}+\left\langle b_{i},b_{i}\right\rangle v_{i}=v_{i}}$

und damit

${\displaystyle v=\sum _{i=1}^{n}\left\langle b_{i},v\right\rangle b_{i}.}$

Im Beispiel 2 oben gilt für den Vektor ${\displaystyle {\vec {v}}={\begin{pmatrix}2\\7\end{pmatrix}}}$:

${\displaystyle \left\langle {\vec {b}}_{1},{\vec {v}}\right\rangle ={\frac {3}{5}}\cdot 2+{\frac {4}{5}}\cdot 7={\frac {34}{5}}}$   und

${\displaystyle \left\langle {\vec {b}}_{2},{\vec {v}}\right\rangle =-{\frac {4}{5}}\cdot 2+{\frac {3}{5}}\cdot 7={\frac {13}{5}}}$

und damit

${\displaystyle {\vec {v}}={\frac {34}{5}}\,{\vec {b}}_{1}+{\frac {13}{5}}\,{\vec {b}}_{2}={\frac {34}{5}}\,{\begin{pmatrix}{\tfrac {3}{5}}\\[1ex]{\tfrac {4}{5}}\end{pmatrix}}+{\frac {13}{5}}\,{\begin{pmatrix}-{\tfrac {4}{5}}\\[1ex]{\tfrac {3}{5}}\end{pmatrix}}.}$

Das Skalarprodukt

In Koordinaten bezüglich einer Orthonormalbasis hat jedes Skalarprodukt die Form des Standardskalarprodukts. Genauer:

Ist ${\displaystyle B=\{b_{1},\dots ,b_{n}\}}$ eine Orthonormalbasis von ${\displaystyle V}$ und haben die Vektoren ${\displaystyle v}$ und ${\displaystyle w}$ bezüglich ${\displaystyle B}$ die Koordinatendarstellung ${\displaystyle v=v_{1}b_{1}+\dots +v_{n}b_{n}}$ und ${\displaystyle w=w_{1}b_{1}+\dots +w_{n}b_{n}}$, so gilt

${\displaystyle \langle v,w\rangle =v_{1}w_{1}+\dots +v_{n}w_{n}}$

im reellen Fall, bzw.

${\displaystyle \langle v,w\rangle ={\bar {v}}_{1}w_{1}+\dots +{\bar {v}}_{n}w_{n}}$

im komplexen Fall.

Orthogonale Abbildungen

Ist ${\displaystyle f\colon V\to V}$ eine orthogonale (im reellen Fall) bzw. eine unitäre Abbildung (im komplexen Fall) und ist ${\displaystyle B}$ eine Orthonormalbasis von ${\displaystyle V}$, so ist die Darstellungsmatrix von ${\displaystyle f}$ bezüglich der Basis ${\displaystyle B}$ eine orthogonale bzw. eine unitäre Matrix.

Bezüglich beliebiger Basen ist diese Aussage falsch.

Unendlichdimensionale Räume

Definition

Sei ${\displaystyle (V,\langle \cdot ,\cdot \rangle )}$ ein Prähilbertraum und sei ${\displaystyle \|\cdot \|={\sqrt {\langle \cdot ,\cdot \rangle }}}$ die durch das Skalarprodukt induzierte Norm. Eine Teilmenge ${\displaystyle S\subset V}$ heißt Orthonormalsystem, falls ${\displaystyle \|e\|=1}$ und ${\displaystyle \langle e,f\rangle =0}$ für alle ${\displaystyle e,f\in S}$ mit ${\displaystyle e\neq f}$ gilt.

Ein Orthonormalsystem, dessen lineare Hülle dicht im Raum liegt, heißt Orthonormalbasis oder Hilbertbasis des Raums.

Es ist zu beachten, dass im Sinne dieses Abschnitts, im Gegensatz zur endlichen Dimension, eine Orthonormalbasis keine Hamelbasis, also keine Basis im Sinn der linearen Algebra ist. Das heißt, ein Element aus ${\displaystyle V}$ lässt sich im Allgemeinen nicht als Linearkombination aus endlich vielen Elementen aus ${\displaystyle S}$ darstellen, sondern nur mit abzählbar unendlich vielen, also als unbedingt konvergente Reihe.

Ein Orthonormalsystem ${\displaystyle S=(e_{n})_{n\in \mathbb {N} }}$ heißt vollständig, wenn für alle ${\displaystyle x\in V}$ gilt

${\displaystyle \lim _{n\to \infty }\Vert x-\sum _{k=0}^{n}\langle x,e_{k}\rangle e_{k}\Vert =0}$.

Charakterisierung

Für einen Prähilbertraum ${\displaystyle H}$ sind folgende Aussagen äquivalent:

• ${\displaystyle S\subset H}$ ist eine Orthonormalbasis.
• ${\displaystyle S}$ ist ein Orthonormalsystem und es gilt die parsevalsche Gleichung:

${\displaystyle \|x\|^{2}=\sum _{v\in S}|\langle x,v\rangle |^{2}}$ für alle ${\displaystyle x\in H}$.

Ist ${\displaystyle H}$ sogar vollständig, also ein Hilbertraum, ist dies zusätzlich äquivalent zu:

• Das orthogonale Komplement ${\displaystyle S^{\perp }}$ von ${\displaystyle S}$ ist der Nullraum, denn allgemein gilt für eine Teilmenge ${\displaystyle T}$, dass ${\displaystyle {T^{\perp }}^{\perp }={\overline {\operatorname {span} (T)}}}$.
• Konkreter: Es gilt genau dann ${\displaystyle x=0}$, wenn für alle ${\displaystyle v\in S}$ das Skalarprodukt ${\displaystyle \langle x,v\rangle =0}$ ist.
• ${\displaystyle S}$ ist ein bezüglich der Inklusion maximales Orthonormalsystem, d. h. jedes Orthonormalsystem, das ${\displaystyle S}$ enthält, ist gleich ${\displaystyle S}$. Wäre ein maximales ${\displaystyle S}$ kein Orthonormalsystem, so existierte ein Vektor im orthogonalen Komplement, normierte man dieses und fügte es zu ${\displaystyle S}$ hinzu, erhielte man wiederum ein Orthonormalsystem.

Existenz

Mit dem Lemma von Zorn lässt sich zeigen, dass jeder Hilbertraum ${\displaystyle H}$ eine Orthonormalbasis besitzt: Man betrachte die Menge aller Orthonormalsysteme in ${\displaystyle H}$ mit der Inklusion als partieller Ordnung. Diese ist nichtleer, da die leere Menge ein Orthonormalsystem ist. Jede aufsteigende Kette solcher Orthonormalsysteme bezüglich der Inklusion ist durch die Vereinigung nach oben beschränkt: Denn wäre die Vereinigung kein Orthonormalsystem, so enthielte sie einen nicht normierten oder zwei verschiedene nicht orthogonale Vektoren, die bereits in einem der vereinigten Orthonormalsysteme hätten vorkommen müssen. Nach dem Lemma von Zorn existiert somit ein maximales Orthonormalsystem – eine Orthonormalbasis. Statt aller Orthonormalsysteme kann man auch nur die Orthonormalsysteme, die ein gegebenes Orthonormalsystem enthalten, betrachten. Dann erhält man analog, dass jedes Orthonormalsystem zu einer Orthogonalbasis ergänzt werden kann.

Alternativ lässt sich das Gram-Schmidt-Verfahren auf ${\displaystyle H}$ oder eine beliebige dichte Teilmenge anwenden und man erhält eine Orthonormalbasis.

Jeder separable Prähilbertraum besitzt eine Orthonormalbasis. Hierfür wähle man eine (höchstens) abzählbare dichte Teilmenge und wende auf diese das Gram-Schmidt-Verfahren an. Hierbei ist die Vollständigkeit nicht notwendig, da stets nur Projektionen auf endlichdimensionale Unterräume durchzuführen sind, welche stets vollständig sind. Hierdurch erhält man eine (höchstens) abzählbare Orthonormalbasis. Umgekehrt ist auch jeder Prähilbertraum mit einer (höchstens) abzählbaren Orthonormalbasis separabel.

Entwicklung nach einer Orthonormalbasis

Ein Hilbertraum ${\displaystyle (H,\langle \cdot ,\cdot \rangle )}$ mit einer Orthonormalbasis ${\displaystyle S}$ hat die Eigenschaft, dass für jedes ${\displaystyle v\in H}$ die Reihendarstellung

${\displaystyle v=\sum _{u\in S}\langle u,v\rangle u}$

gilt. Diese Reihe konvergiert unbedingt. Ist der Hilbertraum endlichdimensional, so fällt der Begriff der unbedingten Konvergenz mit dem der absoluten Konvergenz zusammen. Diese Reihe nennt man auch verallgemeinerte Fourier-Reihe. Wählt man nämlich den Hilbertraum ${\displaystyle L^{2}([0,2\pi ])}$ der reellwertigen quadratintegrierbaren Funktionen mit dem Skalarprodukt

${\displaystyle \langle f,g\rangle =\int _{0}^{2\pi }f(x)g(x)\,\mathrm {d} x,}$

dann ist

${\displaystyle S=\{c_{0}\}\cup \{c_{n},s_{n}\mid n\in \mathbb {N} \}}$

mit

${\displaystyle c_{0}(x)={\frac {1}{\sqrt {2\pi }}},\ c_{n}(x)={\frac {1}{\sqrt {\pi }}}\cos(nx),\ s_{n}(x)={\frac {1}{\sqrt {\pi }}}\sin(nx)}$ für ${\displaystyle x\in [0,2\pi ]}$ und ${\displaystyle n\in \mathbb {N} }$

ein Orthonormalsystem und sogar eine Orthonormalbasis von ${\displaystyle L^{2}([0,2\pi ])}$. Bezüglich dieser Basis sind

${\displaystyle \left\langle f,c_{0}\right\rangle ={\frac {1}{\sqrt {2\pi }}}\int _{0}^{2\pi }f(x)\,\mathrm {d} x,}$

${\displaystyle \left\langle f,c_{n}\right\rangle ={\frac {1}{\sqrt {\pi }}}\int _{0}^{2\pi }f(x)\cos(nx)\,\mathrm {d} x}$

und

${\displaystyle \left\langle f,s_{n}\right\rangle ={\frac {1}{\sqrt {\pi }}}\int _{0}^{2\pi }f(x)\sin(nx)\,\mathrm {d} x,\quad n\in \mathbb {N} }$

gerade die Fourier-Koeffizienten der Fourier-Reihe von ${\displaystyle f}$. Daher ist die Fourier-Reihe gerade die Reihendarstellung eines Elements aus ${\displaystyle L^{2}([0,2\pi ])}$ bezüglich der gegebenen Orthonormalbasis.

Weitere Beispiele

Sei ${\displaystyle \ell ^{2}}$ der Folgenraum der quadratsummierbaren Folgen. Die Menge ${\displaystyle S=\{e_{n}\colon n\in \mathbb {N} \}}$ ist eine Orthonormalbasis von ${\displaystyle \ell ^{2}}$.

Literatur

• Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-03217-0.
• Dirk Werner: Funktionalanalysis. 6., korrigierte Auflage. Springer-Verlag, Berlin 2007, ISBN 978-3-540-72533-6, S. 222–236.