Quadratische Gleichung

Eine quadratische Gleichung ist eine Gleichung, die sich in der Form

${\displaystyle ax^{2}+bx+c=0\quad }$

mit ${\displaystyle a\neq 0}$ schreiben lässt. Hierbei sind ${\displaystyle a,b,c}$ Koeffizienten; ${\displaystyle x}$ ist die Unbekannte der Gleichung. In der Mathematik, bzw. genauer der Algebra, interessiert man sich für die Lösungen von quadratischen Gleichungen (aber auch allgemeineren Gleichungen). Das bedeutet, dass für die Unbekannte ${\displaystyle x}$ all jene Zahlen gefunden werden sollen, durch die, wenn man ${\displaystyle x}$ durch sie ersetzt, eine wahre Aussage wie ${\displaystyle 0=0}$ entsteht. Ein Beispiel ist die quadratische Gleichung ${\displaystyle x^{2}-4=0}$. Auflösen dieser ergibt, dass ${\displaystyle x=2}$ und ${\displaystyle x=-2}$ die Lösungsmenge bilden. Durch eine Probe kann dies schnell mit den Grundrechenarten nachvollzogen werden: Es gilt ${\displaystyle 2^{2}=4}$ und ${\displaystyle (-2)^{2}=(-2)\cdot (-2)=4}$, also ${\displaystyle (\pm 2)^{2}-4=4-4=0}$, womit wegen ${\displaystyle x^{2}-4=0}$ die wahre Aussage ${\displaystyle 0=0}$ entsteht. Alle anderen Werte für ${\displaystyle x}$ werden im Gegensatz dazu nach Einsetzen stets zu ${\displaystyle x^{2}-4\not =0}$ führen, also die Gleichung nicht lösen. Daher ist die Lösungsmenge von ${\displaystyle x^{2}-4=0}$ genau gegeben durch ${\displaystyle \{-2,2\}}$. Ist wie in diesem Beispiel zusätzlich ${\displaystyle b=0}$, spricht man bei ${\displaystyle ax^{2}+c=0}$ von einer reinquadratischen Gleichung.

Die Lösungen einer allgemeinen quadratischen Gleichung ${\displaystyle ax^{2}+bx+c=0}$ lassen sich anhand der Formel

${\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$

explizit bestimmen. Umgangssprachlich wird diese auch als Mitternachtsformel bezeichnet. Es bezeichnet das Symbol ${\displaystyle {\sqrt {}}}$ die Quadratwurzel. Im Bereich der reellen Zahlen kann eine quadratische Gleichung keine, eine oder zwei Lösungen besitzen. Ist der Ausdruck ${\displaystyle b^{2}-4ac}$ unter der Wurzel negativ, so existiert keine Lösung; ist er Null, so existiert eine Lösung; wenn er positiv ist, so existieren zwei Lösungen. Insbesondere lässt sich die Anzahl der Lösungen einer quadratischen Gleichung oberer Form bereits durch eine Untersuchung der Größe ${\displaystyle b^{2}-4ac}$, auch genannt Diskriminante, bestimmen, ohne die Lösungen selbst genau berechnen zu müssen.

Die linke Seite der Gleichung ${\displaystyle ax^{2}+bx+c=0}$ ist der Term einer quadratischen Funktion (allgemeiner ausgedrückt: ein Polynom zweiten Grades) ${\displaystyle f(x)=ax^{2}+bx+c}$; der Funktionsgraph dieser Funktion im kartesischen Koordinatensystem ist eine Parabel. Geometrisch beschreibt die quadratische Gleichung ${\displaystyle f(x)=0}$ – falls vorhanden – die Nullstellen dieser Parabel.

Konkrete Anwendungen haben quadratische Gleichungen etwa in Situationen der elementaren Geometrie, da quadratische Terme mit Flächeninhalten von Rechtecken korrespondieren können. In der modernen Mathematik, aber auch im Umfeld mathematischer Modelle, tauchen sie in ihrer einfachsten Form hingegen eher selten auf, oder sind lediglich ein einfacher Spezialfall einer weitaus umfangreicheren Theorie (etwa jene der algebraischen Gleichungen oder quadratischen Formen). Dennoch gehören quadratische Gleichungen und ihre Auflösung fest zum Lehrplan an vielen Schulen weltweit, da sie Beispiele von Gleichungen sind, die mit in der Schulmathematik zugänglichen Mitteln behandelbar sind, was auf die meisten Gleichungen nicht zutrifft. Dahinter steckt auch der Gedanke, Schüler auf den Themenkomplex „Gleichungen“ im Allgemeinen anhand eines Beispiels vorzubereiten.

In der höheren Algebra bzw. algebraischen Zahlentheorie werden quadratische Gleichungen auch über anderen Körpern betrachtet. Im Falle der komplexen Zahlen haben sie stets mindestens eine Lösung, womit der in der reellen Situation mögliche Fall „keine Lösung“ entfällt. Im Fall endlicher Primkörper führt die Frage nach Lösbarkeit zum quadratischen Reziprozitätsgesetz.

Einführung

Es ist

${\displaystyle 3=3}$

ein Beispiel für eine wahre Gleichung: Beide Zahlen auf jeder Seite des Gleichheitszeichens sind identisch. Gleichungen können umgeformt werden. Dahinter steckt die Idee, dass, wenn zwei identische Größen auf identische Weise manipuliert werden, die Resultate wieder identisch sein müssen. Aus beidseitiger Addition von ${\displaystyle 3=3}$ mit ${\displaystyle 7}$ geht ${\displaystyle 10=10}$ hervor – wieder eine gültige Gleichung. Oft beinhalten Gleichungen eine Unbekannte, etwa

${\displaystyle 2\cdot x=4.}$

Beidseitige Division durch ${\displaystyle 2}$ formt dies zu ${\displaystyle x=2}$ um, womit die Unbekannte plötzlich „sichtbar“ wird. Im Nachhinein ist auch der einfache Zusammenhang ${\displaystyle 2\cdot 2=4}$ leicht zu prüfen, und es war ${\displaystyle x=2}$ der „einzige Kandidat“, der mit ${\displaystyle 2\cdot x=4}$ schon unausweichlich bestimmt war. In vielen Problemen der wissenschaftlichen Praxis entstehen aus bekannten Beziehungen zunächst unbekannter Größen Gleichungen, weshalb Techniken zu deren Auflösen große Bedeutung zukommt. Die innerhalb einer wissenschaftlichen Theorie erarbeiteten kausalen Zusammenhänge oder ökonomische Forderungen „zwingen“ die Größen in einen begrenzten Raum an Möglichkeiten, doch erst ein Auflösen der entstehenden Gleichungen macht diese wenigen Möglichkeiten „sichtbar“.

Ein Beispiel ist: Ein rechteckiges Zimmer ist zwei Meter länger als breit und hat den Flächeninhalt ${\displaystyle 24}$ Quadratmeter – wie lang und wie breit ist es? Die Frage führt zur Gleichung

${\displaystyle x\cdot (x+2)=24\qquad }$ (${\displaystyle x}$ = Breite des Zimmers in Metern),

also

${\displaystyle x^{2}+2x=24.}$

Dies ist Beispiel einer quadratischen Gleichung. Will man diese auflösen, müssen beidseitig so oft Umformungen vorgenommen werden, bis das ${\displaystyle x}$ isoliert auf einer Seite steht (und auf der anderen Seite der oder die möglichen Werte, die die Gleichung lösen). Bei quadratischen Gleichungen erweisen sich die binomischen Formeln als nützlich. Die Grundidee ist, „umgekehrt“ zu denken: Schafft man es, irgendwo einen Term der Form ${\displaystyle x^{2}+2bx+b^{2}}$ zu erzeugen, kann eine Gleichung vereinfacht werden. Dies erfordert ein gewisses Geschick beim „Erkennen“ und zu Beginn meist etwas Übung. Im obigen Beispiel kann auf der linken Seite durch Hinzufügen eines nichtigen Terms ${\displaystyle 1-1=0}$ wie folgt eine binomische Formel „erzwungen“ werden:

${\displaystyle x^{2}+2x=24\iff x^{2}+2x\,\,+\underbrace {1-1} _{{\text{keine}} \atop {\text{Veränderung}}}=24\iff (x^{2}+2x+1)-1=24\iff (x+1)^{2}-1=24{\overset {|\,+1}{\iff }}(x+1)^{2}=25.}$

Nun muss nur noch auf beiden Seiten die Quadratwurzel in beiden Zweigen ${\displaystyle {\sqrt {25}}=\pm 5}$ gezogen werden (was letztlich der entscheidende Schritt zum „Auflösen“ der Gleichung ist), um aus

${\displaystyle x+1=\pm 5}$

die Lösungsmenge ${\displaystyle \{-6,4\}}$ zu erhalten. Damit hat das Zimmer die Breite ${\displaystyle x=4}$.^{[Anm. 1]} Dies war schon seit Aufstellung der Bedingungen an das Zimmer „unausweichlich“, wurde aber erst nach Auflösung der quadratischen Gleichung für Geist und Auge „sichtbar“.

Allgemeine Form – Normalform – Nullform

Die allgemeine Form der quadratischen Gleichung lautet

${\displaystyle ax^{2}+bx+c=0\qquad (a\neq 0)\ .}$

Dabei heißt ${\displaystyle ax^{2}}$ quadratisches Glied, ${\displaystyle bx}$ lineares Glied und ${\displaystyle c}$ konstantes Glied (auch Absolutglied) der Gleichung.

Die Gleichung ist in Normalform, falls ${\displaystyle a=1}$, wenn also das quadratische Glied den Koeffizienten 1 hat. Aus der allgemeinen Form lässt sich die Normalform durch Äquivalenzumformungen gewinnen, indem durch ${\displaystyle a\neq 0}$ dividiert wird. Mit der Definition

${\displaystyle p={\frac {b}{a}}}$   und   ${\displaystyle \displaystyle q={\frac {c}{a}}}$

lässt sich die Normalform somit schreiben als

${\displaystyle x^{2}+px+q=0\ .}$

Steht auf einer Seite einer Gleichung die 0, wird diese auch Nullform genannt.^[1]

Im Folgenden werden zunächst quadratische Gleichungen mit reellen Zahlen als Koeffizienten ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ bzw. als ${\displaystyle p}$ und ${\displaystyle q}$ betrachtet.

Lösungen der quadratischen Gleichung mit reellen Koeffizienten

Eine Lösung einer quadratischen Gleichung ist eine Zahl, die die Gleichung erfüllt, wenn sie für ${\displaystyle x}$ eingesetzt wird. Jede quadratische Gleichung hat, wenn man komplexe Zahlen als Lösungen zulässt, genau zwei (gegebenenfalls zusammenfallende) Lösungen, auch Wurzeln der Gleichung genannt. Betrachtet man nur die reellen Zahlen, so hat eine quadratische Gleichung null bis zwei Lösungen.

Anzahl der reellen Nullstellen

Die Anzahl der Lösungen lässt sich mit Hilfe der sog. Diskriminante ${\displaystyle D}$ bestimmen. Im allgemeinen Fall ist ${\displaystyle D=b^{2}-4ac}$, im normierten Fall ist ${\displaystyle D=p^{2}-4q}$ (zur Herleitung siehe unten):

Die Grafik zeigt den Zusammenhang zwischen der Anzahl der reellen Nullstellen und der Diskriminante:

• A Diskriminante positiv: Die Parabel hat zwei Schnittpunkte mit der ${\displaystyle x}$-Achse, es gibt also zwei verschiedene reelle Nullstellen ${\displaystyle x_{1}}$ und ${\displaystyle x_{2}\ .}$
• B Diskriminante Null: Die Parabel hat genau einen Berührpunkt mit der ${\displaystyle x}$-Achse, nämlich ihren Scheitelpunkt. Es gibt somit genau eine (doppelte) reelle Lösung. Die quadratische Gleichung ${\displaystyle ax^{2}+bx+c=0}$ lässt sich auf die Form ${\displaystyle a\cdot (x-x_{1})^{2}=0}$ bringen.
• C Diskriminante negativ: Die Parabel hat keinen Schnittpunkt mit der ${\displaystyle x}$-Achse, es gibt keine reellen Lösungen der quadratischen Gleichung. Lässt man komplexe Zahlen als Grundmenge für die Lösungen zu, erhält man zwei verschiedene komplexe Lösungen. Diese sind zueinander konjugiert, das heißt, sie haben den gleichen Realteil und ihre Imaginärteile unterscheiden sich nur durch das Vorzeichen.

Einfache Spezialfälle

Ist der Koeffizient des linearen Gliedes ${\displaystyle b=0}$ oder das absolute Glied ${\displaystyle c=0}$, so lässt sich die quadratische Gleichung durch einfache Äquivalenzumformungen lösen, ohne dass eine allgemeine Lösungsformel benötigt würde.

Fehlendes lineares Glied

Die reinquadratische Gleichung ${\displaystyle ax^{2}+c=0}$ mit ${\displaystyle a\neq 0}$ ist äquivalent zu

${\displaystyle x^{2}=-{\frac {c}{a}}\ .}$

Die Lösungen lauten

${\displaystyle x_{1,2}=\pm {\sqrt {-{\frac {c}{a}}}}\ .}$

Im Fall ${\displaystyle a\cdot c<0\,}$ existieren zwei Lösungen. Im Fall ${\displaystyle a\cdot c>0\,}$ existieren keine reellen Lösungen. Die komplexen Lösungen sind dann

${\displaystyle x_{1,2}=\pm \mathrm {i} {\sqrt {\frac {c}{a}}}\ .}$

Zum Beispiel hat die Gleichung ${\displaystyle x^{2}-3=0}$ die Lösungen ${\displaystyle x_{1,2}=\pm {\sqrt {3}}}$. Die Gleichung ${\displaystyle 2x^{2}+8=0}$ hat keine reellen Lösungen, die komplexen Lösungen lauten ${\displaystyle x_{1,2}=\pm 2\mathrm {i} }$.

Der Fall ${\displaystyle a\cdot c=0}$ und wegen ${\displaystyle a\neq 0}$ damit ${\displaystyle c=0\,}$, also eine doppelte Lösung, tritt nur bei Gleichungen vom Typ ${\displaystyle ax^{2}=0}$ mit ${\displaystyle a\neq 0}$ ein und sie lautet ${\displaystyle x_{1}=0}$.

Fehlendes konstantes Glied

Aus der Gleichung ${\displaystyle ax^{2}+bx=0}$ ergibt sich durch Ausklammern ${\displaystyle x(ax+b)=0}$, d. h., es muss ${\displaystyle x=0}$ oder ${\displaystyle ax+b=0}$ gelten. Die beiden Lösungen lauten also

${\displaystyle x_{1}=0}$  und  ${\displaystyle x_{2}=-{\frac {b}{a}}\ .}$

Zum Beispiel hat die Gleichung ${\displaystyle 3x^{2}-2x=0}$ die Lösungen ${\displaystyle x_{1}=0}$ und ${\displaystyle x_{2}={\tfrac {2}{3}}}$.

Gleichung in Scheitelpunktform

Die Scheitelpunktform

${\displaystyle a(x-d)^{2}+e=0}$

ist eine Variation der reinquadratischen Gleichung ${\displaystyle ax^{2}+c=0}$. Sie kann wie diese durch „Rückwärtsrechnen“ gelöst werden: Zunächst subtrahiert man ${\displaystyle e}$ und dividiert durch ${\displaystyle a}$. Dies führt zu

${\displaystyle (x-d)^{2}=-{\frac {e}{a}}\ .}$

Für ${\displaystyle -{\frac {e}{a}}\geq 0}$ ergibt sich daraus

${\displaystyle x-d=\pm {\sqrt {-{\frac {e}{a}}}}}$

Durch Addition von ${\displaystyle d}$ erhält man die Lösungen

${\displaystyle x_{1}=d+{\sqrt {-{\frac {e}{a}}}}}$  und  ${\displaystyle x_{2}=d-{\sqrt {-{\frac {e}{a}}}}\ .}$

Für ${\displaystyle -{\frac {e}{a}}<0}$ erhält man entsprechend die beiden komplexen Lösungen

${\displaystyle x_{1}=d+\mathrm {i} {\sqrt {\frac {e}{a}}}}$  und  ${\displaystyle x_{2}=d-\mathrm {i} {\sqrt {\frac {e}{a}}}\ .}$

Beispiel:

${\displaystyle {\begin{aligned}3(x-2)^{2}-5&=0&&|+5;:3\\(x-2)^{2}&={\frac {5}{3}}&&|\pm {\sqrt {\ }}\\x-2&=\pm {\sqrt {\frac {5}{3}}}&&|+2\\x&=2\pm {\sqrt {\frac {5}{3}}}\end{aligned}}}$

Lösen mit quadratischer Ergänzung

Beim Lösen mit quadratischer Ergänzung werden die binomischen Formeln benutzt, um eine quadratische Gleichung in allgemeiner Form oder in Normalform auf die Scheitelpunktform zu bringen, die dann einfach aufgelöst werden kann.

Man verwendet die erste bzw. zweite binomische Formel in der Form ${\displaystyle (x\pm d)^{2}=x^{2}\pm 2dx+d^{2}\ .}$

Dazu wird die quadratische Gleichung so umgeformt, dass die linke Seite die Form ${\displaystyle x^{2}\pm 2dx}$ hat. Danach wird auf beiden Seiten ${\displaystyle d^{2}}$ addiert. Dies ist die „quadratische Ergänzung“. Die linke Seite hat nun die Gestalt ${\displaystyle x^{2}\pm 2dx+d^{2}}$ und kann mit der binomischen Formel zu ${\displaystyle (x\pm d)^{2}}$ umgeformt werden. Danach liegt die Gleichung in der leicht aufzulösenden Scheitelpunktform vor.

Dies wird am besten anhand eines konkreten Zahlenbeispiels erklärt. Betrachtet wird die quadratische Gleichung

${\displaystyle 3x^{2}-15x+18=0\ .}$

Zunächst wird die Gleichung normiert, indem man durch den Leitkoeffizienten (hier 3) dividiert:

${\displaystyle x^{2}-5x+6=0\ .}$

Das konstante Glied (hier 6) wird auf beiden Seiten subtrahiert:

${\displaystyle x^{2}-5x=-6\ .}$

Nun folgt die eigentliche quadratische Ergänzung: Die linke Seite muss so ergänzt werden, dass sich eine binomische Formel (hier die zweite) rückwärts anwenden lässt. Das ${\displaystyle d}$ aus der obigen binomischen Formel ist dann ${\displaystyle {\tfrac {5}{2}}}$, also muss auf beiden Seiten der Gleichung ${\displaystyle d^{2}=\left({\tfrac {5}{2}}\right)^{2}}$ addiert werden:

${\displaystyle x^{2}-5x+\left({\frac {5}{2}}\right)^{2}=\left({\frac {5}{2}}\right)^{2}-6\ .}$

Die linke Seite wird nach der binomischen Formel umgeformt, die rechte Seite vereinfacht:

${\displaystyle \left(x-{\frac {5}{2}}\right)^{2}={\frac {1}{4}}\ .}$

Dies führt zu

${\displaystyle x-{\frac {5}{2}}=\pm {\frac {1}{2}}}$ ,

also zu den beiden Lösungen ${\displaystyle x_{1}={\frac {5}{2}}+{\frac {1}{2}}=3}$  und  ${\displaystyle x_{2}={\frac {5}{2}}-{\frac {1}{2}}=2\ .}$

Allgemeine Lösungsformeln

Man kann quadratische Gleichungen auch lösen, indem man eine der mit Hilfe der quadratischen Ergänzung hergeleiteten allgemeinen Lösungsformeln verwendet.

Lösungsformel für die allgemeine quadratische Gleichung (a-b-c-Formel)

Die Lösungen der allgemeinen quadratischen Gleichung ${\displaystyle ax^{2}+bx+c=0}$ lauten:

${\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ }$.

Die Formel wird in Teilen Deutschlands und der Schweiz umgangssprachlich als Mitternachtsformel bezeichnet, weil „Schüler sie aufsagen können sollen, selbst wenn man sie um Mitternacht weckt und nach der Formel fragt“.^[2] In Österreich ist der Ausdruck große Lösungsformel gebräuchlich.^[3]

Alternative Formen

Alternative Formulierungen der a-b-c-Formel, die mehr der weiter unten behandelten p-q-Formel ähneln, sind:

${\displaystyle x_{1,2}={\frac {-b}{2a}}\pm {\sqrt {\frac {b^{2}-4ac}{4a^{2}}}}=-{\frac {\ b}{2a}}\pm {\sqrt {\left(-{\frac {\ b}{2a}}\right)^{2}-{\frac {c}{a}}}}\ }$

Wenn man die quadratische Gleichung in der Form

${\displaystyle ax^{2}+2\beta x+c=0}$

angibt (d. h. mit ${\displaystyle \beta =b/2}$), erhält man die etwas einfachere Lösungsformel:

${\displaystyle x_{1,2}={\frac {-\beta \pm {\sqrt {\beta ^{2}-ac}}}{a}}}$

Durch Erweitern der a-b-c-Formel mit dem Term ${\displaystyle -b\mp {\sqrt {b^{2}-4ac}}}$ erhält man eine Formel, welche auch für den linearen Fall ${\displaystyle a=0}$ anwendbar ist, dafür jedoch im Fall ${\displaystyle c=0}$ die Berechnung der Lösung ${\displaystyle x={\frac {-b}{a}}}$ wegen einer Division durch Null nicht mehr liefern kann. In beiden Fällen wird die Lösungsformel ohnehin nicht benötigt. Für betragsmäßig sehr kleine ${\displaystyle a}$ ist die alternative Form jedoch robuster gegenüber numerischer Auslöschung.

${\displaystyle x_{1,2}={\frac {\left(-b\pm {\sqrt {b^{2}-4ac}}\right)\cdot \left(-b\mp {\sqrt {b^{2}-4ac}}\right)}{2a\cdot \left(-b\mp {\sqrt {b^{2}-4ac}}\right)}}={\frac {2c}{-b\mp {\sqrt {b^{2}-4ac}}}}}$

Lösung der a-b-c-Formel bei negativer Diskriminante

Ist die oben eingeführte Diskriminante ${\displaystyle D=b^{2}-4ac}$ negativ, so ist für die Lösungen die Wurzel einer negativen Zahl zu berechnen. Im Zahlbereich der reellen Zahlen gibt es hierfür keine Lösungen. Im Bereich der komplexen Zahlen gilt ${\displaystyle {\sqrt {D}}=\mathrm {i} {\sqrt {-D}}}$. Dieser Term bestimmt den Imaginärteil der beiden zueinander konjugierten Lösungen, einmal mit positivem, einmal mit negativem Vorzeichen. Der Term davor mit ${\displaystyle -{\tfrac {b}{2a}}}$ wird zum konstanten Realteil der beiden Lösungen:

${\displaystyle x_{1,2}=-{\frac {b}{2a}}\pm \mathrm {i} {\frac {\sqrt {4ac-b^{2}}}{2a}}=-{\frac {\ b}{2a}}\pm \mathrm {i} {\sqrt {\,{\Bigg |}\!\left(-{\frac {\ b}{2a}}\right)^{2}-{\frac {c}{a}}{\Bigg |}}}\ }$ (komplexer Fall bei negativer Diskriminante).

Herleitung der a-b-c-Formel

Aus der allgemeinen Form ergibt sich durch Umformen nach dem Verfahren der quadratischen Ergänzung:

${\displaystyle {\begin{array}{rcll}ax^{2}+bx+c&=&0&|-c\\[1ex]ax^{2}+bx&=&-c&|{}\cdot 4a\\[1ex]4a^{2}x^{2}+4abx&=&-4ac&|+b^{2}{\text{ (quadratische Ergänzung)}}\\[1ex](2ax)^{2}+2\cdot 2ax\,b+b^{2}&=&b^{2}-4ac&|{\text{ Umformen mit binomischer Formel}}\\[1ex](2ax+b)^{2}&=&b^{2}-4ac&|\pm {\sqrt {\quad }}\\[1ex]2ax+b&=&\pm {\sqrt {b^{2}-4ac}}&|-b\\[1ex]2ax&=&-b\pm {\sqrt {b^{2}-4ac}}&|:(2a)\\[1ex]x&=&{\dfrac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}&\end{array}}}$

Rechenbeispiel

Bei der quadratischen Gleichung

${\displaystyle x^{2}-x-1=0}$

ist ${\displaystyle a=1,b=-1}$ und ${\displaystyle c=-1}$. Durch Einsetzen dieser Werte in die a-b-c-Formel erhält man die Lösungen

${\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}={\frac {-(-1)\pm {\sqrt {(-1)^{2}-4\cdot 1\cdot (-1)}}}{2\cdot 1}}={\frac {1\pm {\sqrt {5}}}{2}}}$.

Lösungsformel für die Normalform (p-q-Formel)

Bei Vorliegen der Normalform ${\displaystyle x^{2}+px+q=0}$ lauten die Lösungen nach der p-q-Formel:

${\displaystyle x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}}$

In Österreich ist diese Formel als kleine Lösungsformel bekannt.^[3]

Lösung der p-q-Formel bei negativer Diskriminante

Wie bei der a-b-c-Formel gibt es, wenn ${\displaystyle {\tfrac {1}{4}}D=\left({\tfrac {p}{2}}\right)^{2}-q}$ negativ ist, im Zahlbereich der reellen Zahlen keine Lösungen. Die komplexen Lösungen ergeben sich dann zu:

${\displaystyle x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {-1}}\cdot {\sqrt {\frac {-D}{4}}}}$

${\displaystyle x_{1,2}=-{\frac {p}{2}}\pm \mathrm {i} {\sqrt {\,q-\!\left({\frac {p}{2}}\right)^{\!2}}}}$

Herleitung der p-q-Formel

Die Formel ergibt sich aus der Normalform der quadratischen Gleichung durch quadratische Ergänzung:

${\displaystyle {\begin{array}{rcll}x^{2}+px+q&=&0&|-q\\[1ex]x^{2}+px&=&-q&|+\left({\dfrac {p}{2}}\right)^{2}{\text{ (quadratische Ergänzung)}}\\[1ex]x^{2}+2\cdot {\dfrac {p}{2}}\ x+\left({\dfrac {p}{2}}\right)^{2}&=&\left({\dfrac {p}{2}}\right)^{2}-q&|{\text{ binomische Formel}}\\[1ex]\left(x+{\dfrac {p}{2}}\right)^{2}&=&\left({\dfrac {p}{2}}\right)^{2}-q&|{\text{ Wurzel ziehen}}\\[1ex]\left|x+{\dfrac {p}{2}}\right|&=&{\sqrt {\left({\dfrac {p}{2}}\right)^{2}-q}}&|{\text{ Betrag auflösen}}\\[1ex]x+{\dfrac {p}{2}}&=&\pm {\sqrt {\left({\dfrac {p}{2}}\right)^{2}-q}}&|-{\dfrac {p}{2}}\\[1ex]x&=&-{\dfrac {p}{2}}\pm {\sqrt {\left({\dfrac {p}{2}}\right)^{2}-q}}\end{array}}}$

Eine andere Möglichkeit, die Formel herzuleiten, besteht darin, dass man in der a-b-c-Formel ${\displaystyle a=1}$, ${\displaystyle b=p}$ und ${\displaystyle c=q}$ setzt und den Nenner 2 in die Wurzel hineinzieht.

Zerlegung in Linearfaktoren

Mit den Lösungen lässt sich das quadratische normierte Polynom in Linearfaktoren zerlegen:

${\displaystyle x^{2}+px+q=(x-x_{1})\cdot (x-x_{2})}$

und das nicht normierte in

${\displaystyle ax^{2}+bx+c=a\cdot (x-x_{1})\cdot (x-x_{2})\ .}$

Satz von Vieta

Liegt die quadratische Gleichung in Normalform vor und hat die Lösungen ${\displaystyle x_{1}}$ und ${\displaystyle x_{2}}$, so gilt

${\displaystyle 0=x^{2}+px+q=(x-x_{1})\cdot (x-x_{2})=x^{2}-(x_{1}+x_{2})x+x_{1}x_{2}\ .}$

Durch Koeffizientenvergleich erhält man den Satz von Vieta

${\displaystyle \,x_{1}+x_{2}=-p}$  und  ${\displaystyle x_{1}\cdot x_{2}=q\ .}$

Insbesondere wenn ${\displaystyle p}$ und ${\displaystyle q}$ ganze Zahlen sind, lassen sich so durch Ausprobieren, ob Teilerpaare von ${\displaystyle q}$ als Summe ${\displaystyle -p}$ ergeben, mit einiger Übung oft die Lösungen rasch finden. Beispielsweise erhält man für ${\displaystyle x^{2}+4x+3=0}$ die Lösungen ${\displaystyle x_{1}=-1}$ und ${\displaystyle x_{2}=-3}$ durch die Zerlegung ${\displaystyle 3=(-1)(-3)}$ mit ${\displaystyle (-1)+(-3)=-4\ .}$

Numerische Berechnung

Wenn die Lösungen numerisch ermittelt werden und sich um Größenordnungen voneinander unterscheiden, kann durch folgende Variation der obigen Formeln das Problem der Auslöschung vermieden werden:

${\displaystyle x_{1}=-{\frac {p}{2}}-\operatorname {sgn}(p)\cdot {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}}$

${\displaystyle x_{2}={\frac {q}{x_{1}}}}$

Hierbei hat ${\displaystyle \operatorname {sgn}(p)}$ den Wert ${\displaystyle -1}$ für ${\displaystyle p<0}$ und sonst den Wert ${\displaystyle 1}$. Die erste Formel ergibt die betragsgrößte Lösung. Die zweite Formel beruht auf dem Satz von Vieta.

Grafische Lösungen

Mithilfe des Carlyle-Kreises

Die Lösungen der Gleichung ${\displaystyle x^{2}+px+q=0}$ sind die Nullstellen der Parabel ${\displaystyle f(x)=x^{2}+px+q}$. Diese erhält man u. a. auch mit Hilfe des Carlyle-Kreises (Bild 1):

• Zeichne in einem kartesischen Koordinatensystem einen Kreis um den Mittelpunkt ${\displaystyle M=\left({\tfrac {-p}{2}}|{\tfrac {q+1}{2}}\right)}$ derart, dass er durch den Punkt ${\displaystyle A(0|1)}$ geht. Die Schnittpunkte mit der X-Achse sind, sofern vorhanden, die reellen Lösungen der Gleichung.

Mithilfe des Steinerschen Kreises

• Auflösung einer quadratischen Gleichung durch bloßes Ziehen von geraden Linien bei Benutzung eines gezeichneten Kreises.^[4]

Die im Folgenden beschriebene Konstruktion ist prinzipiell anwendbar für Lösungen der Gleichungen, in denen ${\displaystyle p}$ und ${\displaystyle q}$ rationale Zahlen sind:

${\displaystyle x^{2}+px+q=0}$,

${\displaystyle x^{2}-px+q=0}$,

${\displaystyle x^{2}+px-q=0}$,

${\displaystyle x^{2}-px-q=0}$.

Die in den Bildern eingezeichneten Parabeln sind nicht Teil der Konstruktion, sie dienen lediglich der Verdeutlichung.

Gegeben sei beispielsweise die Gleichung ${\displaystyle x^{2}-px+q=0}$ (Bild 2):

In einem kartesischen Koordinatensystem wird zuerst der Kreisbogen ${\displaystyle k}$ mit Radius gleich ${\displaystyle 1}$ um den Mittelpunkt ${\displaystyle M(0|1)}$ eingezeichnet und anschließend die zueinander parallelen Tangenten an den Punkten ${\displaystyle A(0|2)}$ und ${\displaystyle B(0|0)}$ eingetragen. Nun sind auf den entsprechenden Tangenten die Punkte ${\displaystyle C\left({\tfrac {4}{p}}|2\right)}$ und ${\displaystyle D\left({\tfrac {q}{p}}|0\right)}$ zu bestimmen. Eine Verbindung des Punktes ${\displaystyle C}$ mit ${\displaystyle D}$ erzeugt auf dem Kreisbogen ${\displaystyle k}$ die Schnittpunkte ${\displaystyle E}$ und ${\displaystyle F}$. Die abschließenden beiden geraden Linien ab Punkt ${\displaystyle A}$ durch ${\displaystyle E}$ und ${\displaystyle F}$ liefern auf der ${\displaystyle x}$-Achse die Punkte ${\displaystyle X_{1}}$ und ${\displaystyle X_{2}}$. Die Längen ${\displaystyle |{\overline {BX_{1}}}|=x_{1}}$ und ${\displaystyle |{\overline {BX_{2}}}|=x_{2}}$ entsprechen den beiden Lösungen der quadratischen Gleichung ${\displaystyle x^{2}-px+q=0}$.

• Für die Lösung der Gleichung ${\displaystyle x^{2}-px-q=0}$ (Bild 3) gilt: ${\displaystyle D\left(-{\tfrac {q}{p}}|0\right)}$ mit ${\displaystyle |{\overline {BX_{1}}}|=-x_{1}}$ und ${\displaystyle |{\overline {BX_{2}}}|=x_{2}}$.

Beispiele

Rechenbeispiel

Für die Gleichung

${\displaystyle 4x^{2}-12x-40=0}$

ergeben sich als Lösungen nach der a-b-c-Formel

${\displaystyle x_{1,2}={\frac {-(-12)\pm {\sqrt {(-12)^{2}-4\cdot 4\cdot (-40)}}}{2\cdot 4}}}$ ,

also ${\displaystyle x_{1}=-2}$ und ${\displaystyle x_{2}=5\ .}$

Zur Nutzung der p-q-Formel wird die allgemeine Form zuerst in die Normalform überführt, indem die Gleichung durch 4 dividiert wird:

${\displaystyle x^{2}-3x-10=0\ .}$

Mit der p-q-Formel ergeben sich die Lösungen

${\displaystyle x_{1,2}=-{\frac {-3}{2}}\pm {\sqrt {\left({\frac {-3}{2}}\right)^{2}-(-10)}}}$ ,

also somit ebenfalls ${\displaystyle x_{1}=-2}$ und ${\displaystyle x_{2}=5\ .}$

Mit Hilfe der Zerlegungen ${\displaystyle -10=(-2)\cdot 5}$ und ${\displaystyle 5-2=3}$ erhält man dieselben Lösungen mit dem Satz von Vieta.

Weitere Beispiele

• ${\displaystyle x^{2}+2x-35=0}$
  Die Diskriminante ist positiv. Es ergeben sich die beiden reellen Lösungen ${\displaystyle x_{1}=-7\,}$ und ${\displaystyle x_{2}=5\ .}$
• ${\displaystyle x^{2}-4x+4=0}$
  Die Diskriminante ist null. Die (doppelte) reelle Lösung ist ${\displaystyle x=2\ .}$
• ${\displaystyle x^{2}+12x+37=0}$
  Die Diskriminante ist negativ, daher gibt es keine reellen Lösungen. Die komplexen Lösungen ergeben sich zu ${\displaystyle x_{1}=-6+i\,}$ und ${\displaystyle x_{2}=-6-i\ .}$

Verallgemeinerungen

Komplexe Koeffizienten

Die quadratische Gleichung

${\displaystyle az^{2}+bz+c=0}$

mit komplexen Koeffizienten ${\displaystyle a,b,c\in \mathbb {C} }$, ${\displaystyle a\neq 0}$ hat stets zwei komplexe Lösungen ${\displaystyle z_{1},z_{2}\in \mathbb {C} }$, die genau dann zusammenfallen, wenn die Diskriminante ${\displaystyle b^{2}-4ac}$ gleich null ist.

Die Lösungen lassen sich wie im reellen Fall durch quadratische Ergänzung oder mit den oben angegebenen Lösungsformeln berechnen. Dabei muss allerdings im Allgemeinen eine Quadratwurzel einer komplexen Zahl berechnet werden.

Beispiel

Für die quadratische Gleichung

${\displaystyle z^{2}-(\mathrm {i} +1)z+\mathrm {i} =0}$

hat die Diskriminante den Wert ${\displaystyle D=-2\mathrm {i} =(\mathrm {i} -1)^{2}}$. Es ergeben sich die beiden Lösungen ${\displaystyle z_{1}=1}$ und ${\displaystyle z_{2}=\mathrm {i} \ .}$

Quadratische Gleichungen in allgemeinen Ringen

Allgemein nennt man in der abstrakten Algebra eine Gleichung der Form

${\displaystyle x^{2}+px+q=0}$

mit Elementen ${\displaystyle p,q}$ eines Körpers oder Rings eine quadratische Gleichung. In Körpern und allgemeiner in Integritätsbereichen hat sie höchstens zwei Lösungen, in beliebigen Ringen kann sie mehr als zwei Lösungen haben.

Falls Lösungen existieren, dann erhält man sie in kommutativen Ringen ebenfalls mit der p-q-Formel, falls die Charakteristik des Ringes ungleich 2 ist. Hierbei sind allerdings alle möglichen Quadratwurzeln der Diskriminante zu berücksichtigen. Für einen endlichen Körper ${\displaystyle \mathbb {F} _{2^{n}}\cong \mathbb {F} _{2}(\varrho )}$ der Charakteristik 2 macht man den Ansatz ${\displaystyle x=\textstyle \sum _{i=0}^{n-1}a_{i}\varrho ^{i}}$ und gelangt mittels ${\displaystyle x^{2}=\textstyle \sum _{i=0}^{n-1}a_{i}\varrho ^{2i}}$ zu einem linearen Gleichungssystem für die n Koeffizienten a_i aus ${\displaystyle \mathbb {F} _{2}}$.

Beispiel

Die quadratische Gleichung

${\displaystyle x^{2}-1=0}$

hat im Restklassenring ${\displaystyle \mathbb {Z} /8\mathbb {Z} }$ die vier Lösungen 1, 3, 5 und 7.

Geschichte

Bereits vor 4000 Jahren im Altbabylonischen Reich wurden Probleme gelöst, die äquivalent sind zu einer quadratischen Gleichung. Zum Beispiel enthält die unter der Inventarnummer BM 34568 im British Museum archivierte Tontafel gemäß der von Otto Neugebauer in den 1930er Jahren gelungenen Keilschrift-Übersetzung als neuntes Problem^[5] die Frage nach den Seitenlängen eines Rechtecks, bei dem die Summe von Länge und Breite 14 ergibt und dessen Fläche gleich 48 ist.^[6]

Zwar lässt der auf der Tontafel dokumentierte Lösungsweg keine Begründung erkennen, aber Zwischenwerte, wie sie auch bei der üblichen Lösungsformel oder äquivalenten geometrischen Überlegungen auftauchen:

Die im Text aufgeführten Zwischenwerte, die auf der Tontafel im babylonischen Sexigesimalsystem notiert sind,^[7] ergeben sich ebenfalls dann, wenn die zugehörige quadratische Gleichung ${\displaystyle x^{2}-14x+48=0}$ mit der üblichen Lösungsformel gelöst wird. Dabei erhält man die beiden Lösungen 8 und 6, die geometrisch den beiden gesuchten Seitenlängen des Rechtecks entsprechen:

${\displaystyle x_{1,2}={\frac {14\pm {\sqrt {196-192}}}{2}}={\frac {14\pm 2}{2}}\ .}$

Nach Høyrup ist davon auszugehen, dass der von den Babyloniern beschrittene Lösungsweg der zitierten und ähnlicher Aufgaben wie schon die Aufgabenstellungen geometrisch motiviert waren.^[8]

Bei den antiken Griechen wurden diverse geometrische Probleme graphisch gelöst, die äquivalent zu quadratischen Gleichungen sind. Zum Beispiel findet man in Euklids Elementen die Aufgabe:

Die Aufgabe entspricht in heutiger Notation der Gleichung

${\displaystyle a(a-x)=x^{2}}$ ,

die man umformen kann zur Gleichung der Rechtecke

${\displaystyle x^{2}+ax=a^{2}\ .}$

Im um 628 entstandenen Buch Brāhmasphuṭasiddhānta („Vervollkommnung der Lehre Brahmas“) des indischen Gelehrten Brahmagupta wurden Lösungsmethoden für quadratische Gleichungen verbal beschrieben. Dabei verwendete Brahmagupta bereits negative Zahlen und deren Rechenregeln wie

Dadurch konnte Brahmagupta Fallunterscheidungen vermeiden, wenn er zur quadratischen Gleichung, die man heute in der Form

${\displaystyle a{x}^{2}+bx=c}$  mit ${\displaystyle a,b,c\in \mathbb {R} }$ und ${\displaystyle a>0}$

notiert, folgenden Lösungsweg beschrieb:

Das entspricht der Lösungsformel

${\displaystyle x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}\ .}$

Wie auch die indisch-arabischen Ziffern fanden die Erkenntnisse der indischen Gelehrten ihre Verbreitung und Fortentwicklung über islamische Wissenschaftler. Eine besonders herausragende Rolle spielte der Mathematiker Al-Chwarizmi, dessen ungefähr um 825 verfasstes Buch al-Kitāb al-muḫtaṣar fī ḥisāb al-ğabr wa-ʾl-muqābala („Das kurzgefasste Buch über die Rechenverfahren durch Ergänzen und Ausgleichen“) erstmals allgemeine Techniken der Behandlung von Gleichungen, wenn auch weiterhin verbal beschrieben, enthält. Mit den Äquivalenzumformungen von Gleichungen, die Al-Chwarizmi ausführlich beschrieb, konnte jede beliebige quadratische Gleichung auf einen von sechs Typen reduziert werden. Sechs Typen waren notwendig, da Al-Chwarizmi anders als Brahmagupta keine negativen Zahlen verwendete.

Al-Chwarizmis Buch enthält zu allen Typen anhand eines Zahlenbeispiels ein geometrisches Lösungsverfahren, sodass nur positive Lösungen möglich sind. In der nachfolgenden Liste bedeutet Wurzel die gesuchte Lösung ${\displaystyle x}$ und Vermögen das Quadrat der Lösung ${\displaystyle x^{2}}$. Ferner bezeichnen ${\displaystyle a,b}$ und ${\displaystyle c}$ nichtnegative Koeffizienten:^[12][13]

• Was anlangt die Vermögen, die gleich sind den Wurzeln (heute: ${\displaystyle ax^{2}=bx}$),
• Was anlangt die Vermögen, die gleich sind der Zahl (heute: ${\displaystyle ax^{2}=c}$),
• Was anlangt die Wurzeln, die gleich sind einer Zahl (heute: ${\displaystyle bx=c}$),
• Was anlangt die Vermögen und die Wurzeln, die gleich sind der Zahl (heute: ${\displaystyle ax^{2}+bx=c}$),
• Was anlangt die Vermögen und die Zahl, die gleich sind den Wurzeln (heute: ${\displaystyle ax^{2}+c=bx}$) und
• Was anlangt die Wurzeln und die Zahl, die gleich sind dem Vermögen (heute: ${\displaystyle ax^{2}=bx+c}$).

Zur Lösung der quadratischen Gleichungen verwendete al-Chwarizmi keine Äquivalenzumformungen, also keine algebraische Argumentation, sondern in Anlehnung an die griechische Tradition geometrische Argumente (siehe Bild 1). Als Beispiel soll die Gleichung, wie sie bei al-Chwarizmi auftritt,^[14][15]

${\displaystyle x^{2}+10x=39}$

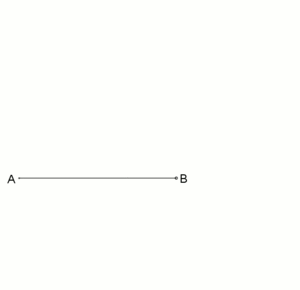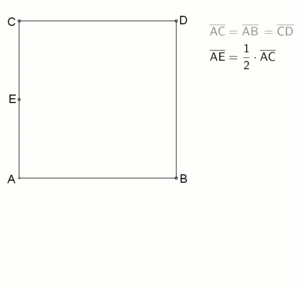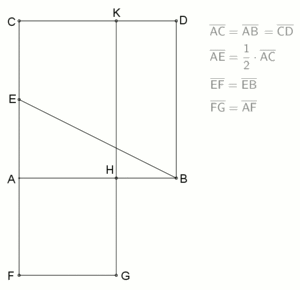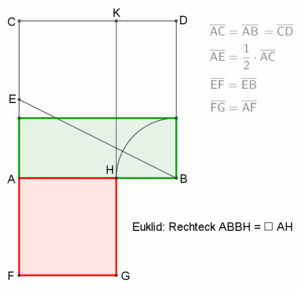
als Spezialfall von ${\displaystyle x^{2}+px=q}$ mit ${\displaystyle p,q>0}$ geometrisch gelöst werden. Man fasst dazu die linke Seite der Gleichung (siehe Bild 2) auf als ein Quadrat EFIH der Seitenlänge ${\displaystyle x}$ (und somit der Fläche ${\displaystyle x^{2}}$) und zwei Rechtecke DEHG und BCFE mit den Seiten ${\displaystyle 5}$ und ${\displaystyle x}$ (und somit jeweils der Fläche ${\displaystyle 5x}$). Das Quadrat und die beiden Rechtecke werden wie im Bild 2 gezeigt zu einem Gnomon mit den Eckpunkten BCIGDE zusammengesetzt. Dieses Gnomon hat nach Voraussetzung eine Fläche von ${\displaystyle x^{2}+10x=39}$. Ergänzt man es mit dem Quadrat ABED der Seitenlänge ${\displaystyle 5}$ (und somit der Fläche ${\displaystyle 25}$) zu dem Quadrat ACIG, so besitzt dieses die Fläche ${\displaystyle 39+25=64}$. Andererseits hat aber dieses Quadrat ACIG nach Konstruktion die Seitenlänge ${\displaystyle 5+x}$ und somit den Flächeninhalt ${\displaystyle (5+x)^{2}}$. Wegen ${\displaystyle 64=8^{2}}$ schließt man ${\displaystyle 5+x=8}$ und somit ${\displaystyle x=3}$. Die quadratische Gleichung wird also »quadratisch ergänzt« zu ${\displaystyle (x+5)^{2}=64}$ mit der (positiven) Lösung ${\displaystyle x=3}$ (siehe Bild 3).^[16] Man beachte, dass man mit dieser geometrischen Methode nicht die negative Lösung ${\displaystyle x=-13}$ erhält.

Bei Heron von Alexandria und auch bei al-Chwarizmi wird die Lösung von

${\displaystyle ax^{2}+bx=c}$

verbal beschrieben; in heutiger Schreibweise als

${\displaystyle x={\frac {{\sqrt {ac+\left({\frac {b}{2}}\right)^{2}}}-{\frac {b}{2}}}{a}}\ .}$

Allerdings schiebt Heron den euklidischen Weg als geometrische Begründung nach.

Um 1145 übersetzte Robert von Chester und etwas später Gerhard von Cremona die Schriften von al-Chwarizmi ins Lateinische.^[17]

Dadurch gelangte die Klassifizierung und die geometrischen Lösungsmethoden nach Europa.

Michael Stiefel verfasste 1544 das Buch Arithmetica integra, das auf das Buch Behend vnnd Hubsch Rechnung durch die kunstreichen regeln Algebre so gemeincklich die Coss genennt werden von Christoph Rudolff aufbaut. Es gelingt dem Autor durch Verwendung negativer Zahlen die Fallunterscheidung für quadratische Gleichungen zu vermeiden. Aber er lässt negative Zahlen noch nicht als Lösungen zu, da er sie als absurd empfindet.^[18]

Einen neuen Ansatz zur Lösung einer quadratischen Gleichung bot der Wurzelsatz von Vieta, der posthum 1615 in seinem Werk De Aequationem Recognitione et Emendatione Tractatus duo publiziert wurde.

Im Jahr 1637 beschrieb René Descartes in seiner Schrift La Géométrie eine Methode zur Lösung quadratischer Gleichungen mit Zirkel und Lineal. Er zeigte weiter, dass Gleichungen höheren Grades im Allgemeinen nicht ausschließlich mit Zirkel und Lineal gelöst werden können.

Siehe auch

• Lineare Gleichung
• Kubische Gleichung
• Quartische Gleichung

Literatur

• Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Springer Verlag, Berlin 2022, ISBN 978-3-662-66286-1.
• Bartel Leendert van der Waerden: Erwachende Wissenschaft. Band 1: Ägyptische, babylonische und griechische Mathematik. 2. Auflage. Birkhäuser 1966.

Weblinks

• Video: Vom Lösen quadratischer Gleichungen – pq-Formel und Mitternachtsformel und der Satz von Vieta. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/17884.

Anmerkungen

1. ↑ Es hat die andere Lösung ${\displaystyle x=-6}$ hier keine sinnvolle Interpretation.

Einzelnachweise

1. ↑ Heiko Tallig: Anwendungsmathematik für Wirtschaftswissenschaftler. Oldenbourg, München/Wien 2006, ISBN 978-3-486-57920-8, S. 29 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 29. Dezember 2020]). 
2. ↑ Guido Walz: Gleichungen und Ungleichungen. Klartext für Nichtmathematiker. Springer, 2018, ISBN 978-3-658-21669-6, S. 14 (eingeschränkte Vorschau in der Google-Buchsuche). 
3. ↑ ^{a b} Franz Embacher: Quadratische Gleichungen. Skript auf mathe-online.at.
4. ↑ August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, V. Abschnitt, Aufgaben ersten und zweiten Grades., §32. Graphische Auflösung der Gleichungen zweiten Grades., S. 175–176, Fig. 137., S. 188–189 (Textarchiv – Internet Archive). 
5. ↑ Das sind die fünf oberen Zeilen der rechten Spalte. Siehe Foto auf der Homepage des British Museums (Gesamtbeschreibung).
6. ↑ Otto Neugebauer: Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, Abteilung A: Quellen, Dritter Band, Dritter Teil. Berlin 1937, S. 14–22 und Tafel 1.
7. ↑ Die Zahlzeichen des Tontafeltextes werden erläutert in Jörg Bewersdorff: Algebra für Einsteiger. Von der Gleichungsauflösung zur Galois-Theorie. 6. Auflage. Wiesbaden 2019, ISBN 978-3-658-26151-1, S. 4, doi:10.1007/978-3-658-26152-8 (eingeschränkte Vorschau in der Google-Buchsuche). 
8. ↑ Jens Høyrup: Lengths, widths, surfaces. A portrait of old Babylonian algebra and its kin. New York 2002, ISBN 978-1-4419-2945-7, S. 393–395, doi:10.1007/978-1-4757-3685-4 (englisch). 
9. ↑ Euklid, Johann Friedrich Lorenz (Übersetzer): Euklids Elemente, funfzehn Bücher. Halle 1781, S. 31–32 (digital.slub-dresden). 
10. ↑ Es gilt auch nach dem Höhensatz: Das Rechteck ABBH und das Quadrat AH haben den gleichen Flächeninhalt
11. ↑ ^{a b} Zitiert nach der Übersetzung von Jörg Bewersdorff: Algebra für Einsteiger. Von der Gleichungsauflösung zur Galois-Theorie. 6. Auflage. Wiesbaden 2019, ISBN 978-3-658-26151-1, S. 6 f., doi:10.1007/978-3-658-26152-8. 
12. ↑ Hans Wußing: 6000 Jahre Mathematik. Band 1. Springer, 2008, ISBN 978-3-540-77189-0, S. 237–241, doi:10.1007/978-3-540-77192-0. 
13. ↑ Helmuth Gericke: Mathematik in Antike, Orient und Abendland. 7. Auflage. Fourier Verlag, 2003, ISBN 3-925037-64-0, S. 198.
14. ↑ Louis Charles Karpinski: Robert of Chester’s Latin translation of the Algebra of al-Khowarizmi. London 1915, S. 77–83 (englisch, online bei archive.org). 
15. ↑ Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 102.
16. ↑ Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 101–102.
17. ↑ Hans Wußing: 6000 Jahre Mathematik. Band 1. Springer, 2008, ISBN 978-3-540-77189-0, S. 278, doi:10.1007/978-3-540-77192-0. 
18. ↑ Hans Wußing: 6000 Jahre Mathematik. Band 1. Springer, 2008, ISBN 978-3-540-77189-0, S. 341–342, doi:10.1007/978-3-540-77192-0.