Loi bêta PERT

Loi bêta PERT
Densité de probabilité
Fonction de répartition
Paramètres	${\displaystyle a<b<c\in \mathbb {R} }$
Support	${\displaystyle x\in [a,c]\,}$
Densité de probabilité	${\displaystyle {\frac {(x-a)^{\alpha -1}(c-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )(c-a)^{\alpha +\beta -1}}}}$ où ${\displaystyle \alpha ={\frac {4b+c-5a}{c-a}}=1+4{\frac {b-a}{c-a}}}$ ${\displaystyle \beta ={\frac {5c-a-4b}{c-a}}=1+4{\frac {c-b}{c-a}}}$
Fonction de répartition	${\displaystyle I_{z}(\alpha ,\beta )}$ (la fonction bêta incomplète régularisée) avec ${\displaystyle z=(x-a)/(c-a)}$
Espérance	${\displaystyle \operatorname {E} [X]={\frac {a+4b+c}{6}}=\mu }$
Médiane	${\displaystyle I_{\frac {1}{2}}^{[-1]}(\alpha ,\beta )(c-a)+a}$ ${\displaystyle \approx a+(c-a){\frac {\alpha -1/3}{\alpha +\beta -2/3}}={\frac {a+6b+c}{8}}}$
Mode	${\displaystyle b}$
Variance	${\displaystyle \operatorname {Var} [X]={\frac {(\mu -a)(c-\mu )}{7}}}$
Asymétrie	${\displaystyle {\frac {2\,(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}}$
Kurtosis normalisé	${\displaystyle {\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}$
modifier

En probabilités et statistiques, les lois bêta PERT sont une famille de lois de probabilité continues définies par la valeur minimale (a), le mode (b) et le maximum (c) qu'une variable peut prendre. Il s'agit d'une transformation de la loi bêta à quatre paramètres avec une hypothèse supplémentaire selon laquelle l'espérance vaut

${\displaystyle \mu ={\frac {a+4b+c}{6}}.}$

La moyenne de la loi est donc définie comme une moyenne pondérée des valeurs minimale, modale et maximale que peut prendre la variable, avec un poids quatre fois plus élevé appliqué à la valeur la plus probable. Cette hypothèse concernant la moyenne a été proposée pour la première fois par Clark en 1962^[1] pour estimer l'effet de l'incertitude de la durée des tâches sur le résultat d'un calendrier de projet évalué à l'aide de la méthode PERT, d'où son nom. Les mathématiques de la loi résultent du souhait des auteurs de rendre l'écart-type égal à environ 1/6 de l'intervalle^[2],[3]. La loi PERT est largement utilisée dans l'analyse des risques ^[4] pour représenter l'incertitude de la valeur d'une certaine quantité lorsque l'on s'appuie sur des estimations subjectives, car les trois paramètres définissant la distribution sont intuitifs pour l'estimateur. La loi bêta PERT est présente dans la plupart des logiciels de simulation.

Comparaison avec la loi triangulaire

La loi bêta PERT offre une alternative ^[5] à l'utilisation de la loi triangulaire qui prend les trois mêmes paramètres. La loi bêta PERT a une forme plus lisse que la loi triangulaire, et cette dernière a une espérance égale à la moyenne des trois paramètres :

${\displaystyle \mu ={\frac {a+b+c}{3}}}$

qui (contrairement à la loi bêta PERT) met autant l'accent sur les valeurs extrêmes qui sont généralement moins connues que la valeur la plus probable, et est donc moins fiable. La loi triangulaire a également une forme angulaire qui ne correspond pas à la forme plus lisse qui caractérise la connaissance subjective.

La loi bêta PERT modifiée

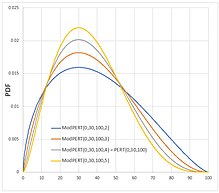
La loi bêta PERT attribue une très faible probabilité aux valeurs extrêmes, en particulier à l'extremum le plus éloigné du mode si la distribution est fortement asymétrique^[6],[7]. La loi bêta PERT modifiée ^[8] a été proposée pour fournir plus de contrôle sur la probabilité attribuée aux valeurs de queue de la distribution. La loi bêta PERT modifiée introduit un quatrième paramètre ${\displaystyle \gamma ,}$ qui contrôle le poids du mode dans la détermination de la moyenne :

${\displaystyle \mu ={\frac {a+\gamma b+c}{\gamma +2}}}$

Généralement, des valeurs comprises entre 2 et 3,5 sont utilisées pour ${\displaystyle \gamma ,}$ et ont pour effet d'aplatir la courbe de densité ; la loi bêta PERT non modifiée correspond donc au cas ${\displaystyle \gamma =4}$. Ceci est utile pour les distributions très asymétriques où les distances ${\displaystyle (b-a),}$ et ${\displaystyle (c-b),}$ sont de tailles très différentes.

La loi bêta PERT modifiée a été implémentée dans plusieurs packages de simulation et langages de programmation :

• ModelRisk ^[9] – complément d’analyse des risques pour Excel.
• Analyse des risques Primavera – outil de simulation d’analyse des risques de projet.
• Tamara ^[10] – outil de simulation d’analyse des risques de projet.
• Wolfram Mathematica ^[11] – programme de calcul symbolique mathématique.
• R (langage de programmation) : package mc2d^[12].
• Python (langage de programmation) : package pertdist^[13]

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « PERT distribution » (voir la liste des auteurs).

• Portail des probabilités et de la statistique