Loi de Kesten-McKay

Cet article est une ébauche concernant les probabilités et la statistique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Loi de Kesten-McKay
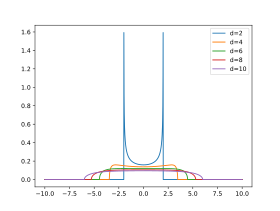Densité de probabilité
Fonction de répartition
Paramètres	${\displaystyle d\in \mathbb {N} \setminus \{0;1\}}$
Support	${\displaystyle ]-2{\sqrt {d-1}},2{\sqrt {d-1}}[}$
Densité de probabilité	${\displaystyle {\frac {d}{2\pi }}{\frac {\sqrt {4(d-1)-x^{2}}}{d^{2}-x^{2}}}1\!\!1_{|x|\leqslant 2{\sqrt {d-1}}}(x)}$
Fonction de répartition	${\displaystyle {\begin{cases}0&{\text{si }}x\leqslant -2{\sqrt {d-1}}\\{\frac {1}{2}}+{\frac {d}{2\pi }}\left[{\scriptstyle \arcsin }\left({\frac {x}{2{\sqrt {d-1}}}}\right)-{\frac {d-2}{d}}{\scriptstyle \arctan }\left({\frac {(d-2)x}{d{\sqrt {4(d-1)-x^{2}}}}}\right)\right]&{\text{si }}|x|\leqslant 2{\sqrt {d-1}}\\1&{\text{si }}x\geqslant 2{\sqrt {d-1}}\end{cases}}}$
Espérance	${\displaystyle 0}$
Médiane	${\displaystyle 0}$
Mode	${\displaystyle 0}$
Asymétrie	${\displaystyle 0}$
modifier

En théorie des probabilités, la loi de Kesten-McKay est une loi de probabilités utilisée en théorie des graphes.

Brendan Kesten établit que pour une suite de graphes aléatoires de degré d ≥ 2 dont l'ordre n tend vers l'infini, les valeurs propres convergent simplement vers la loi de Kesten-McKay. Dans le même article, il montre que cette loi est celle que suivent les valeurs propres de tout graphe régulier étiqueté de degré d.

Définition

La fonction de densité de la loi de Kesten-McKay est :

${\displaystyle f_{KM}(x|d)={\frac {d}{2\pi }}{\frac {\sqrt {4(d-1)-x^{2}}}{d^{2}-x^{2}}}1\!\!1_{|x|\leqslant 2{\sqrt {d-1}}}(x)}$

Il s'agit d'un cas particulier de la loi de Kesten, définie par la densité :

${\displaystyle f_{KM}(x|d,q)={\frac {d}{2\pi }}{\frac {\sqrt {4(q-1)-x^{2}}}{d^{2}-(d-q)x^{2}}}1\!\!1_{|x|\leqslant 2{\sqrt {q}}}(x)}$

Propriétés

Moments

La densité de la loi de Kesten-McKay est paire, donc tous les moments d'ordre impair sont nuls et ceux d'ordre pair valent :

${\displaystyle \mathbb {E} (X^{2k})=d\sum _{i=0}^{k}C(k-1,i)d^{k-i-1}(d-1)^{i}}$

où C(k,i) est un nombre du triangle de Catalan.

Liens avec d'autres lois

Pour d tendant vers l'infini, la loi de Kesten-McKay tend vers la loi du demi-cercle^[1].

Notes

Références

Bibliographie

• (en) Harry Kesten, « Symmetric Random Walks on Groups », Transactions of the American Mathematical Society, American Mathematical Society, vol. 92, n^o 2,‎ août 1959, p. 336-354 (19 pages) (DOI 10.2307/1993160, JSTOR 1993160)
• (en) Brendan D. McKay, « The expected eigenvalue distribution of a large regular graph », Linear Algebra and its Applications, vol. 40,‎ octobre 1981, p. 203-216 (DOI 10.1016/0024-3795(81)90150-6, lire en ligne)
• (en) Pawel J. Szabłowski, « On the Generalized Kesten–McKay Distributions », 2019.
• (en) Matthew de Courcy-Ireland et Michael Magee, « Kesten-McKay Law for the Markoff Surface mod ${\displaystyle p}$ », Annales Henri Lebesgue, vol. 4,‎ 2021, p. 227-250 (lire en ligne)
• (en) Takehiro Hasegawa et Seiken Saito, « A note on the moments of the Kesten distribution », Discrete Mathematics, vol. 344, n^o 10,‎ 10 octobre 2021 (DOI 10.1016/j.disc.2021.112524, lire en ligne)
• (en) Yufei Zhao, « Spectral Distributions of Random Graphs » [PDF], mai 2012

• Portail des probabilités et de la statistique