Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (janvier 2015 ).
Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».
En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?
Inverse-gamma Densité de probabilité Fonction de répartition Paramètres α > 0 {\displaystyle \alpha >0} paramètre de forme (réel ) β > 0 {\displaystyle \beta >0} paramètre d'échelle (réel) Support x ∈ ] 0 ; ∞ [ {\displaystyle x\in \left]0;\infty \right[} Densité de probabilité β α Γ ( α ) x − α − 1 exp ( − β x ) {\displaystyle {\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{-\alpha -1}\exp \left({\frac {-\beta }{x}}\right)} Fonction de répartition Γ ( α , β / x ) Γ ( α ) {\displaystyle {\frac {\Gamma (\alpha ,\beta /x)}{\Gamma (\alpha )}}\!} Espérance β α − 1 {\displaystyle {\frac {\beta }{\alpha -1}}\!} α > 1 {\displaystyle \alpha >1} Mode β α + 1 {\displaystyle {\frac {\beta }{\alpha +1}}\!} Variance β 2 ( α − 1 ) 2 ( α − 2 ) {\displaystyle {\frac {\beta ^{2}}{(\alpha -1)^{2}(\alpha -2)}}\!} α > 2 {\displaystyle \alpha >2} Asymétrie 4 α − 2 α − 3 {\displaystyle {\frac {4{\sqrt {\alpha -2}}}{\alpha -3}}\!} α > 3 {\displaystyle \alpha >3} Kurtosis normalisé 6 5 α − 11 ( α − 3 ) ( α − 4 ) {\displaystyle 6{\frac {5\,\alpha -11}{(\alpha -3)(\alpha -4)}}\!} α > 4 {\displaystyle \alpha >4} Entropie α + ln ( β Γ ( α ) ) − ( 1 + α ) ψ ( α ) {\displaystyle \alpha \!+\!\ln(\beta \Gamma (\alpha ))\!-\!(1\!+\!\alpha )\psi (\alpha )} Fonction génératrice des moments 2 ( − β t ) α 2 Γ ( α ) K α ( − 4 β t ) {\displaystyle {\frac {2\left(-\beta t\right)^{\!\!{\frac {\alpha }{2}}}}{\Gamma (\alpha )}}K_{\alpha }\left({\sqrt {-4\beta t}}\right)} Fonction caractéristique 2 ( − i β t ) α 2 Γ ( α ) K α ( − 4 i β t ) {\displaystyle {\frac {2\left(-\mathrm {i} \beta t\right)^{\!\!{\frac {\alpha }{2}}}}{\Gamma (\alpha )}}K_{\alpha }\left({\sqrt {-4\mathrm {i} \beta t}}\right)} modifier
Dans la théorie des probabilités et en statistiques, la distribution inverse-gamma est une famille de lois de probabilité continues à deux paramètres sur la demi-droite des réels positifs. Il s'agit de l'inverse d'une variable aléatoire distribuée selon une distribution Gamma.
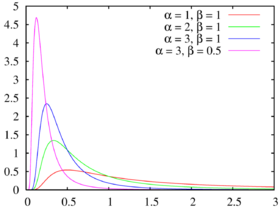
Caractérisation Densité de probabilité La densité de probabilité de la loi inverse-gamma est définie sur le support x > 0 {\displaystyle x>0}
f ( x ; α , β ) = β α Γ ( α ) ( 1 / x ) α + 1 exp ( − β / x ) {\displaystyle f(x;\alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}(1/x)^{\alpha +1}\exp \left(-\beta /x\right)} où α {\displaystyle \alpha } paramètre de forme et β {\displaystyle \beta } paramètre d'échelle .
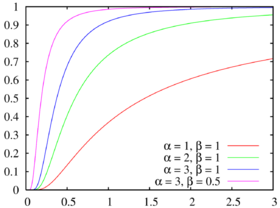
Fonction de répartition La fonction de répartition est la fonction gamma régularisée :
F ( x ; α , β ) = Γ ( α , β / x ) Γ ( α ) {\displaystyle F(x;\alpha ,\beta )={\frac {\Gamma (\alpha ,\beta /x)}{\Gamma (\alpha )}}\!} où le numérateur est la fonction gamma incomplète et le dénominateur est la fonction gamma .
Distributions associées Si X ∼ Inv-Gamma ( α , β ) {\displaystyle X\sim {\mbox{Inv-Gamma}}(\alpha ,\beta )} α = ν 2 , β = 1 2 {\displaystyle \alpha ={\frac {\nu }{2}},\beta ={\frac {1}{2}}} X ∼ Inv-chi-square ( ν ) {\displaystyle X\sim {\mbox{Inv-chi-square}}(\nu )\,} loi inverse-χ² ; Si X ∼ Inv-Gamma ( k , θ ) {\displaystyle X\sim {\mbox{Inv-Gamma}}(k,\theta )\,} 1 / X ∼ Gamma ( k , 1 / θ ) {\displaystyle 1/X\sim {\mbox{Gamma}}(k,1/\theta )\,} loi Gamma de paramètre de forme k {\displaystyle k} 1 / θ {\displaystyle 1/\theta } θ {\displaystyle \theta } Une généralisation multivariée de la loi inverse-gamma est la loi de Wishart inverse . Obtention à partir de la loi Gamma La densité de la loi Gamma est
f ( x ) = x k − 1 e − x / θ θ k Γ ( k ) {\displaystyle f(x)=x^{k-1}{\frac {\mathrm {e} ^{-x/\theta }}{\theta ^{k}\,\Gamma (k)}}} et définissons la transformation Y = g ( X ) = 1 X {\displaystyle Y=g(X)={\frac {1}{X}}}
f Y ( y ) = f X ( g − 1 ( y ) ) | d d y g − 1 ( y ) | {\displaystyle f_{Y}(y)=f_{X}\left(g^{-1}(y)\right)\left|{\frac {\mathrm {d} }{\mathrm {d} y}}g^{-1}(y)\right|} = 1 θ k Γ ( k ) ( 1 y ) k − 1 exp ( − 1 θ y ) 1 y 2 {\displaystyle ={\frac {1}{\theta ^{k}\Gamma (k)}}\left({\frac {1}{y}}\right)^{k-1}\exp \left({\frac {-1}{\theta y}}\right){\frac {1}{y^{2}}}} = 1 θ k Γ ( k ) ( 1 y ) k + 1 exp ( − 1 θ y ) {\displaystyle ={\frac {1}{\theta ^{k}\Gamma (k)}}\left({\frac {1}{y}}\right)^{k+1}\exp \left({\frac {-1}{\theta y}}\right)} = 1 θ k Γ ( k ) y − k − 1 exp ( − 1 θ y ) {\displaystyle ={\frac {1}{\theta ^{k}\Gamma (k)}}y^{-k-1}\exp \left({\frac {-1}{\theta y}}\right)} Remplaçant k {\displaystyle k} α {\displaystyle \alpha } θ − 1 {\displaystyle \theta ^{-1}} β {\displaystyle \beta } y {\displaystyle y} x {\displaystyle x}
f ( x ) = β α Γ ( α ) x − α − 1 exp ( − β x ) {\displaystyle f(x)={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{-\alpha -1}\exp \left({\frac {-\beta }{x}}\right)} Apparitions Références ↑ (en) Mike Ludkovski , « Math 526: Brownian Motion Notes », UC Santa Barbara, 2007 p. 5-6 Portail des probabilités et de la statistique 
![{\displaystyle x\in \left]0;\infty \right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55dd122b5b90a05c3f6460ffa690aaf6a2d80322)
Portail des probabilités et de la statistique 
