Distribució PERT

PERT

Funció de densitat de probabilitat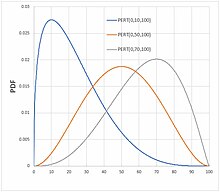
Funció de distribució de probabilitat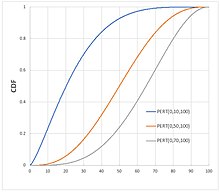
Tipus	distribució de probabilitat
Paràmetres	${\displaystyle b>a\,}$ (real) ${\displaystyle c>b\,}$ (real)
Suport	${\displaystyle x\in [a,c]\,}$
fdp	${\displaystyle {\frac {(x-a)^{\alpha -1}(c-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )(c-a)^{\alpha +\beta -1}}}}$ on ${\displaystyle \alpha ={\frac {4b+c-5a}{c-a}}=1+4{\frac {b-a}{c-a}}}$ ${\displaystyle \beta ={\frac {5c-a-4b}{c-a}}=1+4{\frac {c-b}{c-a}}}$
FD	${\displaystyle I_{z}(\alpha ,\beta )}$ (la funció beta incompleta) regularitzada amb ${\displaystyle z=(x-a)/(c-a)}$
Esperança matemàtica	${\displaystyle \operatorname {E} [X]={\frac {a+4b+c}{6}}=\mu }$
Mediana	${\displaystyle I_{\frac {1}{2}}^{[-1]}(\alpha ,\beta )(c-a)+a}$ ${\displaystyle \approx a+(c-a){\frac {\alpha -1/3}{\alpha +\beta -2/3}}={\frac {a+6b+c}{8}}}$
Moda	${\displaystyle b}$
Variància	${\displaystyle \operatorname {var} [X]={\frac {(\mu -a)(c-\mu )}{7}}}$
Coeficient de simetria	${\displaystyle {\frac {2\,(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}}$
Curtosi	${\displaystyle {\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}$

En probabilitat i estadística, la distribució PERT és una família de distribucions de probabilitat contínues definides pels valors mínim (a), molt probable (b) i màxim (c) que pot prendre una variable. És una transformació de la distribució beta de quatre paràmetres amb una suposició addicional que el seu valor esperat és ^[1]

${\displaystyle \mu ={\frac {a+4b+c}{6}}.}$

Per tant, la mitjana de la distribució es defineix com la mitjana ponderada dels valors mínims, més probables i màxims que pot prendre la variable, amb quatre vegades el pes aplicat al valor més probable. Aquesta hipòtesi sobre la mitjana es va proposar per primera vegada a Clark, 1962 per estimar l'efecte de la incertesa de la durada de les tasques sobre el resultat d'un calendari de projecte avaluat mitjançant la tècnica d'avaluació i revisió del programa, d'aquí el seu nom. Les matemàtiques de la distribució van resultar del desig dels autors de fer que la desviació estàndard sigui igual a aproximadament 1/6 de l'interval.^[2]

• 
  Comparació de corbes de densitat per a les distribucions de probabilitat PERT i triangulars

La distribució PERT s'utilitza àmpliament en l'anàlisi de riscos per representar la incertesa del valor d'alguna quantitat on es basa en estimacions subjectives, perquè els tres paràmetres que defineixen la distribució són intuïtius per a l'estimador. La distribució PERT es presenta a la majoria d'eines de programari de simulació.^[3]

Comparació amb la distribució triangular

La distribució PERT ofereix una alternativa a utilitzar la distribució triangular que pren els mateixos tres paràmetres. La distribució PERT té una forma més llisa que la distribució triangular. La distribució triangular té una mitjana igual a la mitjana dels tres paràmetres:

${\displaystyle \mu ={\frac {a+b+c}{3}}}$

que (a diferència del PERT) posa igual èmfasi en els valors extrems que solen ser menys coneguts que el valor més probable i, per tant, és menys fiable. La distribució triangular també té una forma angular que no coincideix amb la forma més suau que caracteritza el coneixement subjectiu.

Usos ^[4]

La distribució PERT modificada s'ha implementat en diversos paquets de simulació i llenguatges de programació:

• ModelRisk: complement d'anàlisi de riscos per a Excel.
• Anàlisi de riscos Primavera: eina de simulació d'anàlisi de riscos de projectes.
• Tamara: eina de simulació d'anàlisi de riscos del projecte.
• Wolfram Mathematica: programa de càlcul simbòlic matemàtic.
• R (llenguatge de programació): paquet mc2d.
• Python (llenguatge de programació): paquet pertdist.

Referències