Distribució de Cantor

Distribució de Cantor

Funció de distribució de probabilitat
Tipus	Distribució singular i distribució de probabilitat contínua
Epònim	Georg Cantor
Paràmetres	none
Suport	Conjunt de Cantor
Esperança matemàtica	1/2
Mediana	en qualsevol lloc dins de [1/3, 2/3]
Moda	n/a
Variància	1/8
Coeficient de simetria	0
Curtosi	−8/5
FC	${\displaystyle e^{it/2}\prod _{k=1}^{\infty }\cos \left({\frac {t}{3^{k}}}\right)}$

La distribució Cantor és una probabilitat sobre els nombres reals, concentrada en el conjunt de Cantor, que té per funció de distribució la funció de Cantor.

Com que la funció de Cantor és contínua però no absolutament contínua, la distribució de Cantor no té part absolutament contínua respecte la mesura de Lebesgue (no té densitat) ni té part discreta; és un exemple de distribució singular.

En tot aquest article, ${\displaystyle X}$ designarà una variable aleatòria amb distribució de Cantor i ${\displaystyle C}$ el conjunt de Cantor.

Definició

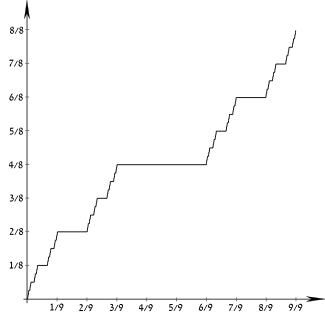
La funció de Cantor és una funció ${\displaystyle F:[0,1]\longrightarrow [0,1]}$ no decreixent, contínua i amb ${\displaystyle F(0)=0}$ i ${\displaystyle F(1)=1}$. Podem estendre-la a una funció definida en tot ${\displaystyle \mathbb {R} }$ (utilitzem la mateixa lletra) ${\displaystyle F:\mathbb {R} \longrightarrow [0,1]}$ posant ${\displaystyle F(x)=0}$ si ${\displaystyle x<0}$, i ${\displaystyle F(x)=1}$ si ${\displaystyle x>1}$. Aleshores ${\displaystyle F}$ és una funció de distribució, i per tant, determina una probabilitat a ${\displaystyle \mathbb {R} }$. Una variable aleatòria ${\displaystyle X}$ que tingui aquesta funció de distribució es diu que té (o segueix) una distribució de Cantor . Atès que ${\displaystyle F}$ és contínua, tindrem que per a qualsevol punt ${\displaystyle x}$

on ${\displaystyle F(x^{-})}$ és el límit per l'esquerra de ${\displaystyle F}$ en el punt ${\displaystyle x}$. Llavors, la distribució de Cantor no té part de salts.^[1]

Per ${\displaystyle a<b}$ tindrem

Atès que la funció de Cantor compleix ${\displaystyle F'(x)=0}$, per a tot ${\displaystyle x\in \mathbb {R} \backslash C}$, on ${\displaystyle C}$ és el conjunt de Cantor, que té ${\displaystyle C}$ mesura de Lebesgue zero, es dedueix que a distribució de Cantor no té densitat,^[1] és a dir, no existeix cap funció ${\displaystyle f\geq 0}$ tal que

Suport de la distribució de Cantor

El suport de la distribució de Cantor és el conjunt de Cantor, que designarem per ${\displaystyle C}$. És a dir, si ${\displaystyle X}$ és una variable aleatòria amb distribució de Cantor, aleshores ${\displaystyle P(X\in C)=1}$. De fet, ${\displaystyle C}$ és el suport tancat de la distribució de Cantor: ${\displaystyle C}$ és el conjunt tancat més petit que té probabilitat 1.

Atès que el conjunt ${\displaystyle C}$ té mesura de Lebesgue zero, la distribució de Cantor és un exemple de distribució singular respecte la mesura de Lebesgue^[2]

Caracterització de la distribució de Cantor

Recordem que el conjunt de Cantor ${\displaystyle C}$ és la intersecció

on Per a cada nivell ${\displaystyle n\geq 1}$ designem per ${\displaystyle I_{1}^{n},\,I_{2}^{n},\dots ,I_{2^{n}}^{n}}$, els intervals que formen ${\displaystyle C_{n}}$. Per exemple, per ${\displaystyle n=2}$,

Propietat. La distribució de Cantor és l'única distribució de probabilitat ^[3] tal que per qualsevol ${\displaystyle n\geq 1}$,

Simetria de la distribució de Cantor

Del fet que el gràfic de la funció de Cantor ${\displaystyle F}$ és simètric respecte el punt (1/2, 1/2) es dedueix que la distribució de Cantor és simètrica respecte del punt 1/2, o equivalentment, que si ${\displaystyle X}$ té una distribució de Cantor, llavors ${\displaystyle 1-X}$ també.

Autosemblança de la distribució de Cantor

Aquesta propietat reposa en el caràcter fractal del conjunt ${\displaystyle C}$. Diu que si seleccionem a l'atzar un dels intervals ${\displaystyle I_{1}^{1}\ {\text{i}}\ I_{2}^{1}}$ que formen ${\displaystyle C_{1}}$, i prenem allí un punt d'acord amb la distribució de Cantor, tornem a obtenir la distribució de Cantor. En fórmules: siguin ${\displaystyle X_{1}\ {\text{i}}\ X_{2}}$ dues variables aleatòries independents, ambdues amb distribució de Cantor, i definim la variable aleatòria ${\displaystyle Y}$ per:

Aleshores ${\displaystyle Y}$ també té distribució de Cantor.^[4] Noteu que ${\displaystyle X_{1}/3\in I_{1}^{1}\ {\text{i}}\ X_{2}/3+2/3\in I_{2}^{1}}$. Per escriure de manera més compacta l'expressió anterior, introduïm una variable aleatòria que representi l'elecció a l'atzar entre ${\displaystyle I_{1}^{1}\ {\text{i}}\ I_{2}^{1}}$. Concretament, sigui ${\displaystyle Z}$ una variable tal que

independent de ${\displaystyle X_{1}\ {\text{i}}\ X_{2}}$; quan ${\displaystyle Z=1}$, elegim ${\displaystyle I_{1}^{1}}$ i quan ${\displaystyle Z=0}$ elegim ${\displaystyle I_{1}^{1}}$:

Escrit en una línia, Observació. El nom autosemblança prové d'una propietat important del conjunt de Cantor,^[5] i aquí en fem una versió probabilística. No s'ha de confondre amb la propietat d'autosimilitud de certs processos estocàstics.

Moments

Atès que ${\displaystyle C\subset [0,1]}$, tenim que ${\displaystyle 0\leq X\leq 1}$, d'on ${\displaystyle X}$ té moments de tots els ordres. De fet, la distribució de Cantor està determinada pels seus moments ^[6]

Esperança

Del fet que ${\displaystyle X}$ i ${\displaystyle 1-X}$ tenen ambdues distribucions de Cantor, es dedueix que

d'on

Moment de 2n ordre i variància

De la propietat d'autosemblança tenim

d'on, aïllant,

D'aquí s'obté:

$${\displaystyle \operatorname {var} (X)=E[X^{2}]-{\big (}E[X]{\big )}^{2}={\frac {1}{8}}.}$$

Fórmula de recurrència pels moments

Utilitzant la mateixa tècnica que a l'apartat anterior es pot trobar una fórmula de recurrència per als moments.^[4] Escrivim

Llavors,

Així, a partir de ${\displaystyle m_{0}=1}$, tenim

Expressió explicita dels moments

Lad and Taylor ^[4] donen la següent expressió pel moment d'ordre ${\displaystyle n}$ :

on la segona suma es fa sobre totes les ${\displaystyle n}$-ples ${\displaystyle (a_{1},\dots ,a_{k})}$ de nombres naturals més grans o iguals a 1, tals que ${\displaystyle n=\sum _{j=1}^{k}a_{j}}$. A la següent taula hi ha els casos ${\displaystyle n=1,2,3,4}$: Alternativament, es pot trobar una fórmula pels moments a partir del càlcul dels cumulants parells [1] Arxivat 2015-12-02 a Wayback Machine.

${\displaystyle \kappa _{2n}={\frac {2^{2n-1}(2^{2n}-1)B_{2n}}{n\,(3^{2n}-1)}},\,\!}$

on B_2n és el segon nombre de Bernoulli, i llavors expressant els moments com a funcions dels cumulants.

Funció característica

Utilitzant també la propietat d'autosemblança es pot calcular la funció característica de la distribució de Cantor:^[7]

La distribució de Cantor com a límit d'una passejada aleatòria

Considerem una successió de variables aleatòries ${\displaystyle X_{1},\,X_{2},\dots }$ independents i totes amb la següent distribució:

Definim la sèrie

que convergeix absolutament q.s., ja que és una sèrie de termes positius i

Calculant la funció característica de ${\displaystyle S}$ es veu que té distribució de Cantor.^[8]

Bibliografia

• Falconer, K. J.. Geometry of Fractal Sets. Cambridge & New York: Cambridge Univ Press, 1985. 
• Hu, Tian-You; Lau, Ka Sing. Fourier Asymptotics of Cantor Type Measures at Infinity. 130, 2002, p. 2711–2717. 
• Knill, O. Probability Theory & Stochastic Processes. India: Overseas Press, 2006. 
• Mandelbrot, B. The Fractal Geometry of Nature. San Francisco, CA: WH Freeman & Co., 1982. 
• Mattilla, P. Geometry of Sets in Euclidean Spaces. San Francisco: Cambridge University Press, 1995. 
• Saks, Stanislaw. Theory of the Integral. Warsaw: PAN, 1933.  (Reprinted by Dover Publications, Mineola, NY.

Enllaços externs

• Morrison, Kent. «Random Walks with Decreasing Steps». Department of Mathematics, California Polytechnic State University, 23-07-1998. Arxivat de l'original el 2015-12-02. [Consulta: 16 febrer 2007].
• Utzet, Frederic. «Una passejada aletòria pel conjunt de Cantor». Department de matemátiques, Universitat Autònoma de Barcelona, Materials Matemàtics, vol. 2020, no. 3, pp. 35, 2020.

Referències