Distribució de Pareto

Distribució de Pareto

Funció de densitat de probabilitat Funcions de densitat de probabilitat de Pareto de tipus I per diferents valors de ${\displaystyle \alpha }$ amb ${\displaystyle x_{\mathrm {m} }=1.}$ A mesura que ${\displaystyle \alpha \rightarrow \infty ,}$ la distribució tendeix a ${\displaystyle \delta (x-x_{\mathrm {m} }),}$ on ${\displaystyle \delta }$ és la funció delta de Dirac.
Funció de distribució de probabilitat Funcions de distribució acumulada de Pareto de tipus I per diferents valors de ${\displaystyle \alpha }$ amb ${\displaystyle x_{\mathrm {m} }=1.}$
Tipus	família exponencial, Distribució de cua pesada i Distribució de Pareto generalitzada
Epònim	Vilfredo Pareto
Paràmetres	${\displaystyle x_{\mathrm {m} }>0}$ escala (real) ${\displaystyle \alpha >0}$ escala (real)
Suport	${\displaystyle x\in [x_{\mathrm {m} },\infty )}$
fdp	${\displaystyle {\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}}$
FD	${\displaystyle 1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }}$
Esperança matemàtica	${\displaystyle {\begin{cases}\infty &{\text{per }}\alpha \leq 1\\{\dfrac {\alpha x_{\mathrm {m} }}{\alpha -1}}&{\text{per }}\alpha >1\end{cases}}}$
Mediana	${\displaystyle x_{\mathrm {m} }{\sqrt[{\alpha }]{2}}}$
Moda	${\displaystyle x_{\mathrm {m} }}$
Variància	${\displaystyle {\begin{cases}\infty &{\text{per }}\alpha \leq 2\\{\dfrac {x_{\mathrm {m} }^{2}\alpha }{(\alpha -1)^{2}(\alpha -2)}}&{\text{per }}\alpha >2\end{cases}}}$
Coeficient de simetria	${\displaystyle {\frac {2(1+\alpha )}{\alpha -3}}{\sqrt {\frac {\alpha -2}{\alpha }}}{\text{ per }}\alpha >3}$
Curtosi	${\displaystyle {\frac {6(\alpha ^{3}+\alpha ^{2}-6\alpha -2)}{\alpha (\alpha -3)(\alpha -4)}}{\text{ per }}\alpha >4}$
Entropia	${\displaystyle \log \left(\left({\frac {x_{\mathrm {m} }}{\alpha }}\right)\,e^{1+{\tfrac {1}{\alpha }}}\right)}$
FC	${\displaystyle \alpha (-ix_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t)}$
Informació de Fisher	${\displaystyle {\mathcal {I}}(x_{\mathrm {m} },\alpha )={\begin{bmatrix}{\dfrac {\alpha }{x_{\mathrm {m} }^{2}}}&-{\dfrac {1}{x_{\mathrm {m} }}}\\-{\dfrac {1}{x_{\mathrm {m} }}}&{\dfrac {1}{\alpha ^{2}}}\end{bmatrix}}}$ Dreta: ${\displaystyle {\mathcal {I}}(x_{\mathrm {m} },\alpha )={\begin{bmatrix}{\dfrac {\alpha ^{2}}{x_{\mathrm {m} }^{2}}}&0\\0&{\dfrac {1}{\alpha ^{2}}}\end{bmatrix}}}$
Mathworld	ParetoDistribution

La distribució de Pareto, que porta el nom de l'enginyer civil, economista i sociòleg Vilfredo Pareto,^[1] és una distribució de probabilitat que s'utilitza per descriure diferents fenòmens socials, de control de qualitat, científics, geofísics, actuarials i altres tipus de fenòmens observables. Inicialment es va aplicar en la descripció de la distribució de la riquesa a la societat, ja que encaixava amb la tendència que una gran porció de la riquesa és propietat d'una fracció petita de la població.^[2][3] El principi de Pareto o la "regla 80-20" que afirma que "el 80% dels efectes són conseqüència del 20% de les causes" també porta el nom de Pareto, tot i que el concepte és diferent, i només les distribució de Pareto amb paràmetre de forma (α) de log₄5 ≈ 1.16 reflecteixen aquest precís cas. Observacions empíriques han demostrat que aquesta distribució 80-20 encaixa un ampli espectre de casos, inclosos fenòmens naturals^[4] i activitats humanes.^[5]

Definicions

Sigui X una variable aleatòria que segueix una distribució de Pareto (de tipus I),^[6] llavors la probabilitat que X sigui més gran que un cert nombre x, és a dir funció de supervivència ve donada per

${\displaystyle {\overline {F}}(x)=\Pr(X>x)={\begin{cases}\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&x\geq x_{\mathrm {m} },\\1&x<x_{\mathrm {m} },\end{cases}}}$

on x_m és el valor mínim possible (necessàriament positiu) de X, i α és un paràmetre positiu. La distribució de Pareto de tipus I és caracteritzada pel paràmetre d'escala x_m i pel paràmetre de forma α, que és conegut com índex de cua (de l'anglès tail index). Quan s'utilitza aquesta distribució per modelar la distribució de la riquesa, llavors el paràmetre α s'anomena índex de Pareto.

Funció de distribució acumulada

A partir de la definició, la funció de distribució acumulada d'una variable aleatòria de Pareto amb paràmetres α i x_m és

${\displaystyle F_{X}(x)={\begin{cases}1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&x\geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\end{cases}}}$

Funció de densitat de probabilitat

Del resultat anterior se'n desprèn (aplicant la diferenciació) que la funció de densitat de probabilitat és

${\displaystyle f_{X}(x)={\begin{cases}{\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}&x\geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\end{cases}}}$

Quan es representa en eixos lineals, la distribució pren una forma de corba en J i tendeix als eixos ortogonals asimptòticament. Tots els segments de la corba són similars entre ells (més enllà d'un factor d'escala). Quan s'empra la representació logarítmica, la distribució és una línea recta.

Propietats

Moments i funció característica

• L'esperança d'una variable aleatòria que segueix la distribució de Pareto és

${\displaystyle \operatorname {E} (X)={\begin{cases}\infty &\alpha \leq 1,\\{\frac {\alpha x_{\mathrm {m} }}{\alpha -1}}&\alpha >1.\end{cases}}}$

• La variància d'una variable aleatòria que segueix una distribució de Pareto és

${\displaystyle \operatorname {Var} (X)={\begin{cases}\infty &\alpha \in (1,2],\\\left({\frac {x_{\mathrm {m} }}{\alpha -1}}\right)^{2}{\frac {\alpha }{\alpha -2}}&\alpha >2.\end{cases}}}$

(Si α ≤ 1, la variància no existeix.)

• Els moments són

${\displaystyle \mu _{n}'={\begin{cases}\infty &\alpha \leq n,\\{\frac {\alpha x_{\mathrm {m} }^{n}}{\alpha -n}}&\alpha >n.\end{cases}}}$

• La funció generadora de moments només és definida per valors no positius de t ≤ 0 com

${\displaystyle M\left(t;\alpha ,x_{\mathrm {m} }\right)=\operatorname {E} \left[e^{tX}\right]=\alpha (-x_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-x_{\mathrm {m} }t)}$

${\displaystyle M\left(0,\alpha ,x_{\mathrm {m} }\right)=1.}$

• La funció característica ve donada per

${\displaystyle \varphi (t;\alpha ,x_{\mathrm {m} })=\alpha (-ix_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t),}$

on Γ(a, x) és la funció gamma incompleta.

Es poden resoldre els paràmetres usant el mètode dels moments.^[7]

Mitjana geomètrica

La mitjana geomètrica (G) és^[8]

${\displaystyle G=x_{\text{m}}\exp \left({\frac {1}{\alpha }}\right).}$

Mitjana harmònica

La mitjana harmònica (H) és^[8]

${\displaystyle H=x_{\text{m}}\left(1+{\frac {1}{\alpha }}\right).}$

Representació gràfica

La distribució corbada amb forma de 'llarga cua' característica que s'obté quan es representa en escala lineal emmascara la simplicitat subjacent de la funció quan es representa logarítmicament, cas en què es mostra com una línea recta amb pendent negatiu. Deriva de la fórmula de la funció de densitat de probabilitat que, per x ≥ x_m,

${\displaystyle \log f_{X}(x)=\log \left(\alpha {\frac {x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}\right)=\log(\alpha x_{\mathrm {m} }^{\alpha })-(\alpha +1)\log x.}$

Com que α és positiu, el gradient −(α + 1) és negatiu.

Distribucions relacionades

Distribucions generalitzades de Pareto

Existeix una jerarquia^[6][9] de les distribucions de Pareto conegudes com Tipus I, II, III, IV, i la distribució de Feller–Pareto.^[6][9][10] La distribució de Pareto de Tipus IV conté les distribucions de Pareto de Tipus I–III com a casos particulars. La distribució de Feller–Pareto^[9][11] generalitza la distribució de Pareto de Tipus IV.

Pareto de tipus I-IV

La jerarquia de les diferents distribucions de Pareto és resumida en la següent taula, en què es comparen les diferents funcions de supervivència.

Quan μ = 0, la distribució de Pareto de Tipus II és també coneguda com la distribució Lomax.^[12]

En aquesta secció, el símbol x_m, utilitzat prèviament per indicar el valor mínim de x, és substituït per σ.

Distribució Pareto

	${\displaystyle {\overline {F}}(x)=1-F(x)}$	Dominii	Paràmetres
Tipus I	${\displaystyle \left[{\frac {x}{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq \sigma }$	${\displaystyle \sigma >0,\alpha }$
Tipus II	${\displaystyle \left[1+{\frac {x-\mu }{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma >0,\alpha }$
Lomax	${\displaystyle \left[1+{\frac {x}{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq 0}$	${\displaystyle \sigma >0,\alpha }$
Tipus III	${\displaystyle \left[1+\left({\frac {x-\mu }{\sigma }}\right)^{1/\gamma }\right]^{-1}}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma ,\gamma >0}$
Tipus IV	${\displaystyle \left[1+\left({\frac {x-\mu }{\sigma }}\right)^{1/\gamma }\right]^{-\alpha }}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma ,\gamma >0,\alpha }$

El paràmetre de forma α és l'índex de cua, μ és la ubicació, σ és l'escala, γ és un paràmetre de desigualtat. Alguns casos particulars de la distribució de Pareto de Tipus IV són

${\displaystyle P(IV)(\sigma ,\sigma ,1,\alpha )=P(I)(\sigma ,\alpha ),}$

${\displaystyle P(IV)(\mu ,\sigma ,1,\alpha )=P(II)(\mu ,\sigma ,\alpha ),}$

${\displaystyle P(IV)(\mu ,\sigma ,\gamma ,1)=P(III)(\mu ,\sigma ,\gamma ).}$

El fet que la mitjana sigui finita i que existeixi la variància i sigui també finita depèn de l'índex de cua α (índex de desigualtat γ). En particular, es mostren a continuació els moments d'ordre δ, que són finits per certs valors de δ > 0, as shown in the table below, on δ no és necessàriament un nombre enter.

Moments de les distribucions de Pareto (cas μ = 0)

	${\displaystyle \operatorname {E} [X]}$	Condició	${\displaystyle \operatorname {E} [X^{\delta }]}$	Condició
Tipus I	${\displaystyle {\frac {\sigma \alpha }{\alpha -1}}}$	${\displaystyle \alpha >1}$	${\displaystyle {\frac {\sigma ^{\delta }\alpha }{\alpha -\delta }}}$	${\displaystyle \delta <\alpha }$
Tipus II	${\displaystyle {\frac {\sigma }{\alpha -1}}+\mu }$	${\displaystyle \alpha >1}$	${\displaystyle {\frac {\sigma ^{\delta }\Gamma (\alpha -\delta )\Gamma (1+\delta )}{\Gamma (\alpha )}}}$	${\displaystyle 0<\delta <\alpha }$
Tipus III	${\displaystyle \sigma \Gamma (1-\gamma )\Gamma (1+\gamma )}$	${\displaystyle -1<\gamma <1}$	${\displaystyle \sigma ^{\delta }\Gamma (1-\gamma \delta )\Gamma (1+\gamma \delta )}$	${\displaystyle -\gamma ^{-1}<\delta <\gamma ^{-1}}$
Tipus IV	${\displaystyle {\frac {\sigma \Gamma (\alpha -\gamma )\Gamma (1+\gamma )}{\Gamma (\alpha )}}}$	${\displaystyle -1<\gamma <\alpha }$	${\displaystyle {\frac {\sigma ^{\delta }\Gamma (\alpha -\gamma \delta )\Gamma (1+\gamma \delta )}{\Gamma (\alpha )}}}$	${\displaystyle -\gamma ^{-1}<\delta <\alpha /\gamma }$

Distribució de Feller-Pareto

William Feller^[9][11] va definir la variable de Pareto a partir de la transformació U = Y⁻¹ − 1 d'una variable aleatòria beta Y, que té com a funció de densitat de probabilitat és

${\displaystyle f(y)={\frac {y^{\gamma _{1}-1}(1-y)^{\gamma _{2}-1}}{B(\gamma _{1},\gamma _{2})}},\qquad 0<y<1;\gamma _{1},\gamma _{2}>0,}$

on B( ) és la funció beta. Si

${\displaystyle W=\mu +\sigma (Y^{-1}-1)^{\gamma },\qquad \sigma >0,\gamma >0,}$

llavors W segueix una distribució de Feller–Pareto FP(μ, σ, γ, γ₁, γ₂).^[6]

Si ${\displaystyle U_{1}\sim \Gamma (\delta _{1},1)}$ i ${\displaystyle U_{2}\sim \Gamma (\delta _{2},1)}$ són variables Gamma independents, una altra possible construcció d'una variable aleatòria de Feller–Pareto (FP) és^[13]

${\displaystyle W=\mu +\sigma \left({\frac {U_{1}}{U_{2}}}\right)^{\gamma }}$

i s'escriu W ~ FP(μ, σ, γ, δ₁, δ₂). Casos especials de distribucions de Feller–Pareto són

${\displaystyle FP(\sigma ,\sigma ,1,1,\alpha )=P(I)(\sigma ,\alpha )}$

${\displaystyle FP(\mu ,\sigma ,1,1,\alpha )=P(II)(\mu ,\sigma ,\alpha )}$

${\displaystyle FP(\mu ,\sigma ,\gamma ,1,1)=P(III)(\mu ,\sigma ,\gamma )}$

${\displaystyle FP(\mu ,\sigma ,\gamma ,1,\alpha )=P(IV)(\mu ,\sigma ,\gamma ,\alpha ).}$

Relació amb la distribució exponencial

La distribució de Pareto està relacionada amb la distribució exponencial. Sigui X una distribució de Pareto amb valor mínim x_m i índex α, llavors

${\displaystyle Y=\log \left({\frac {X}{x_{\mathrm {m} }}}\right)}$

està distribuïda exponencialment amb paràmetre α. Equivalentment, si Y està distribuïda exponencialment amb paràmetre α, llavors

${\displaystyle x_{\mathrm {m} }e^{Y}}$

està distribuïda segons Pareto amb mínim x_m i índex α.

Això es pot demostrar utilitzant tècniques estàndard de canvi de variable:

${\displaystyle {\begin{aligned}\Pr(Y<y)&=\Pr \left(\log \left({\frac {X}{x_{\mathrm {m} }}}\right)<y\right)\\&=\Pr(X<x_{\mathrm {m} }e^{y})=1-\left({\frac {x_{\mathrm {m} }}{x_{\mathrm {m} }e^{y}}}\right)^{\alpha }=1-e^{-\alpha y}.\end{aligned}}}$

La darrera expressió és la funció de distribució acumulada de la distribució exponencial amb paràmetre α.

Es pot construir la distribució de Pareto a parrtir de distribucions exponencials jeràrquiques.^[14] Sigui

${\displaystyle \phi |a\sim {\text{Exp}}(a),\quad \eta |\phi \sim {\text{Exp}}(\phi )}$.

Llavors, ${\displaystyle p(\eta |a)={\frac {a}{(a+\eta )^{2}}}}$.

Relació amb la distribució log-normal

La distribució de Pareto i la distribució log-normal són distribucions alternatives per descriure els mateixos tipus de quantitats. Una de les connexions que hi ha entre elles és que les dues són distribucions que es poden expressar com l'exponenciació d'altres distribucions comunes, de la distribució exponencial i de la distribució normal respectivament. (Vegeu la secció anterior).

Relació amb la distribució generalitzada de Pareto

La distribució de Pareto és un cas particular de la distribució generalitzada de Pareto, que és una família de distribucions que tenen una forma similar, però conté un paràmetre extra de tal forma que el domini de la distribució és o bé fitada per baix (en un punt variable), o bé fitada tant per baix com per dalt (totes dues fites són variables), amb la distribució Lomax com a cas particular. Aquesta família també conté les distribucions exponencials desplaçada i no desplaçada.

La distribució de Pareto amb paràmetre d'escala ${\displaystyle x_{m}}$ i paràmetre de forma ${\displaystyle \alpha }$ és equivalent a la distribució generalitzada de Pareto amb paràmetre d'ubicació ${\displaystyle \mu =x_{m}}$, paràmetre d'escala ${\displaystyle \sigma =x_{m}/\alpha }$ i paràmetre de forma ${\displaystyle \xi =1/\alpha }$. Vice versa, es pot obtenir la distribució de Pareto a partir de la distribució generalitzada de Pareto amb ${\displaystyle x_{m}=\sigma /\xi }$ i ${\displaystyle \alpha =1/\xi }$.

Distribució fitada de Pareto

Fitada de Pareto

Tipus	família exponencial, Distribució de cua pesada i Distribució de Pareto generalitzada
Epònim	Vilfredo Pareto
Paràmetres	${\displaystyle L>0}$ ubicació (real) ${\displaystyle H>L}$ ubicació (real) ${\displaystyle \alpha >0}$ forma (real)
Suport	${\displaystyle L\leqslant x\leqslant H}$
fdp	${\displaystyle {\frac {\alpha L^{\alpha }x^{-\alpha -1}}{1-\left({\frac {L}{H}}\right)^{\alpha }}}}$
FD	${\displaystyle {\frac {1-L^{\alpha }x^{-\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}}$
Esperança matemàtica	${\displaystyle {\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot \left({\frac {\alpha }{\alpha -1}}\right)\cdot \left({\frac {1}{L^{\alpha -1}}}-{\frac {1}{H^{\alpha -1}}}\right),\alpha \neq 1}$ ${\displaystyle {\frac {{H}{L}}{{H}-{L}}}\ln {\frac {H}{L}},\alpha =1}$
Mediana	${\displaystyle L\left(1-{\frac {1}{2}}\left(1-\left({\frac {L}{H}}\right)^{\alpha }\right)\right)^{-{\frac {1}{\alpha }}}}$
Variància	${\displaystyle {\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot \left({\frac {\alpha }{\alpha -2}}\right)\cdot \left({\frac {1}{L^{\alpha -2}}}-{\frac {1}{H^{\alpha -2}}}\right),\alpha \neq 2}$ ${\displaystyle {\frac {2{H}^{2}{L}^{2}}{{H}^{2}-{L}^{2}}}\ln {\frac {H}{L}},\alpha =2}$ (aquest és el segon moment, no la variància)
Coeficient de simetria	${\displaystyle {\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot {\frac {\alpha *(L^{k-\alpha }-H^{k-\alpha })}{(\alpha -k)}},\alpha \neq j}$ (aquest és el moment k-èssim, no l'asimetria)
Mathworld	ParetoDistribution

La distribució fitada (o truncada) de Pareto té tres paràmetres: α, L i H. Com en la distribució estàndard de Pareto, α determina la forma. L denota el valor mínim i H el valor màxim.

La funció de densitat de probabilitat de la distribució fitada de Pareto és

${\displaystyle {\frac {\alpha L^{\alpha }x^{-\alpha -1}}{1-\left({\frac {L}{H}}\right)^{\alpha }}}}$,

on L ≤ x ≤ H i α > 0.

Variables aleatòries que generen distribucions fitades de Pareto

Sigui U una istribució uniforme en (0, 1), llavors, aplicant el mètode de la transformada inversa

${\displaystyle U={\frac {1-L^{\alpha }x^{-\alpha }}{1-({\frac {L}{H}})^{\alpha }}}}$

${\displaystyle x=\left(-{\frac {UH^{\alpha }-UL^{\alpha }-H^{\alpha }}{H^{\alpha }L^{\alpha }}}\right)^{-{\frac {1}{\alpha }}}}$

és una distribució fitada de Pareto.

Distribució simètrica de Pareto

L'objectiu de la distribució simètrica de Pareto i de la distribució zero simètrica de Pareto és capturar algunes distribucions estadístiques especials amb un pic afilat de probabilitat i amb cues de probabilitat simètriques i llargues. Aquestes dues distribucions deriven de la distribució de Pareto. Les cues llargues de probabilitat signifiquen que la probabilitat decau lentament. En molts casos, la distribució de Pareto s'utilitza per ajustar corbes. Però si la distribució té una estructura simètrica amb dues cues que decauen lentament, la distribució de Pareto ja no serveix. És llavors quan s'utilitzen les distribucions simètrica i zero simètrica de Pareto.^[15]

La funció de distribució acumulada de la distribució de Pareto és definida com:^[15]

${\displaystyle F(X)=P(x<X)={\begin{cases}{\tfrac {1}{2}}({b \over 2b-X})^{a}&X<b\\1-{\tfrac {1}{2}}({\tfrac {b}{X}})^{a}&X\geq b\end{cases}}}$

La funció de densitat de probabilitat corresponent és:^[15]

${\displaystyle p(x)={ab^{a} \over 2(b+\left\vert x-b\right\vert )^{a+1}},X\in R}$

La distribució té dos paràmetres: a i b. És simètrica respecte b. Llavors, l'esperança matemàtica és b. La variància és

${\displaystyle E((x-b)^{2})=\int _{-\infty }^{\infty }(x-b)^{2}p(x)dx={2b^{2} \over (a-2)(a-1)}}$

La funció de distribució acumulada de la distribució zero simètrica de Pareto és definida com

${\displaystyle F(X)=P(x<X)={\begin{cases}{\tfrac {1}{2}}({b \over b-X})^{a}&X<0\\1-{\tfrac {1}{2}}({\tfrac {b}{b+X}})^{a}&X\geq 0\end{cases}}}$

Amb funció de densitat de probabilitat

${\displaystyle p(x)={ab^{a} \over 2(b+\left\vert x\right\vert )^{a+1}},X\in R}$

Aquesta distribució és simètrica respecte el zero. El paràmetre està relacionat amb la taxa de caiguda de la probabilitat i representa la magnitud pic de probabilitat.^[15]

Distribució conjunta de Pareto

La distribució (univariable) de Pareto es pot estendre a la distribució conjunta (multivariable) de Pareto.^[16]

Inferència estadística

Estimació de paràmetres

La funció de versemblança dels paràmetre de la distribució de Pareto α i x_m, donada una mostra independent x = (x₁, x₂, ..., x_n), és

${\displaystyle L(\alpha ,x_{\mathrm {m} })=\prod _{i=1}^{n}\alpha {\frac {x_{\mathrm {m} }^{\alpha }}{x_{i}^{\alpha +1}}}=\alpha ^{n}x_{\mathrm {m} }^{n\alpha }\prod _{i=1}^{n}{\frac {1}{x_{i}^{\alpha +1}}}.}$

Per tant, la funció logarítmica de versemblança és

${\displaystyle \ell (\alpha ,x_{\mathrm {m} })=n\ln \alpha +n\alpha \ln x_{\mathrm {m} }-(\alpha +1)\sum _{i=1}^{n}\ln x_{i}.}$

Es pot notar que ${\displaystyle \ell (\alpha ,x_{\mathrm {m} })}$ és monòtonament ascendent amb x_m, és a dir, com més gran és el valor de x_m, més gran serà el valor de la funció de versemblança. Per tant, com que x ≥ x_m, es pot concloure que

${\displaystyle {\widehat {x}}_{\mathrm {m} }=\min _{i}{x_{i}}.}$

Per trobar un estimador per α, es calcula la derivada parcial corresponent i es determina quan és igual a zero:

${\displaystyle {\frac {\partial \ell }{\partial \alpha }}={\frac {n}{\alpha }}+n\ln x_{\mathrm {m} }-\sum _{i=1}^{n}\ln x_{i}=0.}$

Per tant, l'estimador de màxima versemblança per α és:

${\displaystyle {\widehat {\alpha }}={\frac {n}{\sum _{i}\ln(x_{i}/{\widehat {x}}_{\mathrm {m} })}}.}$

L'esperança de l'error estadístic és:^[17]

${\displaystyle \sigma ={\frac {\widehat {\alpha }}{\sqrt {n}}}.}$

Malik (1970)^[18] va donar la distribució conjunta exacta de ${\displaystyle ({\hat {x}}_{\mathrm {m} },{\hat {\alpha }})}$. En particular, ${\displaystyle {\hat {x}}_{\mathrm {m} }}$ i ${\displaystyle {\hat {\alpha }}}$ són independents i ${\displaystyle {\hat {x}}_{\mathrm {m} }}$ és una distribució de Pareto amb paràmetre d'escala x_m i paràmetre de forma nα, mentre ${\displaystyle {\hat {\alpha }}}$ segueix una distribució gamma-inversa amb paràmetres de forma i d'escala n − 1 i nα, respectivament.

Aparició i aplicacions

General

Vilfredo Pareto va utilitzar inicialment aquesta distribució per descriure la distribució de la riquesa entre els individus ja que semblava representar molt bé la manera com una porció gran de la riquesa en tota societat és propietat d'un percentatge petit de la població. També la va usar per desciure la distribució dels ingressos.^[3] La idea és sovint expressada simplement com el principi de Pareto o la "regla del 80-20" que diu que el 20% de la població controla el 80% de la riquesa.^[19] Tanmateix, la regla del 80-20 correspon a un valor particular de α, i de fet, les dades de Pareto dels impostos dels ingressos a Gran Bretanya en el seu Cours d'économie politique indiquen que al voltant del 30% de la població tenia el 70% dels ingressos. La gràfica de la funció de densitat de probabilitat al principi de l'article mostra que la "probabilitat" o fracció de la població que té una quantitat determinada de riquesa (per persona) és més aviat alta quan la quantitat de riquesa és baixa, i que aquesta fracció disminueix de forma contínua a mesura que la riquesa per persona augmenta. Aquesta distribució no es limita a desciure la riquesa o els ingressos, sinó que també es troba en moltes situacions en què es troba un equilibri en la distribució entre allò "petit" i allò "gran". Els següents exemples sovint es considera que segueixen distribucions de Pareto:

• Les mides dels assentaments (hi ha poques ciutats i molts llogarets i pobles)^[20][21]
• La distribució de la mida dels arxius en el tràfic a Internet que utilitza el protocol TCP (hi ha molts més fitxers petits que grans)^[20]
• Taxes d'error dels discs durs^[22]
• Clústers de condensats de Bose-Einstein a prop del zero absolut^[23]

• Les reserves de petroli en els jaciments (hi ha pocs jaciments grans i molts de petits)^[20]
• La distribució en temps computacional de les tasques que fan els supercomputadors (algunes poques de llargues, la majoria curtes)^[24]
• El preu estàndard de retorn a la borsa^[20]
• La mida de les partícules de sorra^[20] així com la mida dels meteorits.
• La severitat de les grans pèrdues en baixes en certes línies de negoci des de responsabilitat genereal, fins a auto comercial i compensació laboral.^[25][26]
• En hidrologia, s'aplica la distribució de Pareto en els esdeveniments extrems com ara la precipitació diària màxima en un any i les descàrregues dels rius.^[27] La figura blava il·lustra un exemple d'ajust de la distribució de Pareto de les precipitacions diàries màximes en un any que mostra també un interval de confiança del 90%, basat en la distribució binomial.

Relació amb la llei de Zipf

La distribució de Pareto és una distribució contínua de probabilitat. La llei de llei de Zipf, també anomenada sovint distribució zeta, és una distirbució discreta que separa els valors en una simple classificació de rangs. Totes dues són una llei de potències amb exponent negatiu, escalats per tal que la seva distribució acumulada sigui igual a 1. Es pot derivar la llei de Zipf de la distribució de Pareto si els valors de ${\displaystyle x}$ (els ingressos) són agrupats en ${\displaystyle N}$ barres talment que el nombre de persones en cada barra segueixi un patró d'1/rang. La distribució és normalitzada definint ${\displaystyle x_{m}}$ tal que ${\displaystyle \alpha x_{\mathrm {m} }^{\alpha }={\frac {1}{H(N,\alpha -1)}}}$ on ${\displaystyle H(N,\alpha -1)}$ és el nombre harmònic generalitzat. Això fa que la funció de densitat de probabilitat de Zipf es pugui derivar de la de Pareto.

${\displaystyle f(x)={\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}={\frac {1}{x^{s}H(N,s)}}}$

on ${\displaystyle s=\alpha -1}$ i ${\displaystyle x}$ és un enter que representa el rang d'1 a N, on N és el grup amb ingressos més alts. Així doncs, una persona seleccionada aleatòriament (o una paraula, un enllaç web, una ciutat...) d'una població (o d'una llengua, d'Internet, d'un país...) té una probabilitat ${\displaystyle f(x)}$ de valdre ${\displaystyle x}$.

Relació amb el "principi de Pareto"

La "llei del 80-20", segons la qual el 20% de les persones més riques obtenen el 80% dels ingressos i que el 20% del 20% de les persones més riques obtenen el 80% del 80% dels ingressos i així successivament aplica exactament quan l'índex val ${\displaystyle \alpha =\log _{4}5={\cfrac {\log _{10}5}{\log _{10}4}}\approx 1.161}$. Es pot derivar aquest resultat a partir de la fórmula de la corba de Lorenz, que s'introdueix més endavant. A més, s'ha demostrat que les següents afirmacions^[28] són matemàticament equivalents:

• Els ingressos estan distribuïts seguint una distribució de Pareto amb índex α > 1.
• Existeix un cert nombre 0 ≤ p ≤ 1/2 tal que el 100p % de la gent rep 100(1 − p)% dels ingressos, i similarment, per tot nombre real (no necessàriament enter) n > 0, el 100pⁿ % de tota la gent reben el 100(1 − p)ⁿ percent dels ingressos. α i p estan relacionades segons

${\displaystyle 1-{\frac {1}{\alpha }}={\frac {\ln(1-p^{n})}{\ln(1-(1-p)^{n})}}}$

Això no només aplica als ingressos, sinó també a la riquesa i a tot allò que es pugui modelar amb aquesta distribució.

Aquí s'exclouen les distribucions en què 0 < α ≤ 1, que, com s'ha notat més amunt, tenen una esperança d'infinit, i per tant no poden modelar raonablement les distribucions d'ingressos.

Relació amb la llei de Price

De vegades s'ofereix la llei de Price com a propietat o com una distribució similar a la de Pareto. Tanmateix, la llei només aplica en el cas ${\displaystyle \alpha =1}$. Noti's que en aquest cas, la quantitat total i l'esperança de la riquesa no estan definides, i la regla només aplica asimptòticament en mostres aleatòries. El principi estès de Pareto, mencionat més amunt, és una regla molt més general.

Corba de Lorenz i coeficient Gini

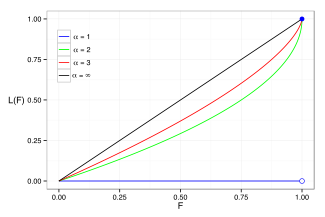
Sovint s'utilitza la corba de Lorenz per caracteritzar els ingreessos i la distribució de la riquesa. En tota distribució, s'escriu la corba de Lorenz L(F) en termes de la funció de distribució f o de la funció de distribució acumulada Fcom

${\displaystyle L(F)={\frac {\int _{x_{\mathrm {m} }}^{x(F)}xf(x)\,dx}{\int _{x_{\mathrm {m} }}^{\infty }xf(x)\,dx}}={\frac {\int _{0}^{F}x(F')\,dF'}{\int _{0}^{1}x(F')\,dF'}}}$

on x(F) és l'inversa de la funció de distribució acumulada. Per la distribució de Pareto,

${\displaystyle x(F)={\frac {x_{\mathrm {m} }}{(1-F)^{\frac {1}{\alpha }}}}}$

i la corba de Lorenz es calcula com

${\displaystyle L(F)=1-(1-F)^{1-{\frac {1}{\alpha }}},}$

Per ${\displaystyle 0<\alpha \leq 1}$ el denominador és infinit i per tant L=0. En la gràfica de la dreta es mostren exemples de la corba de Lorenz per unes quantes distribucions de Pareto.

Segons Oxfam (2016) les 62 persones més riques tenen tanta riquesa com la meitat més pobra de la població mundial.^[29] Es pot estimar l'índex de Pareto que hi hauria en aquesta situació. Sigui ε igual a ${\displaystyle 62/(7\times 10^{9})}$ es té:

${\displaystyle L(1/2)=1-L(1-\varepsilon )}$

o

${\displaystyle 1-(1/2)^{1-{\frac {1}{\alpha }}}=\varepsilon ^{1-{\frac {1}{\alpha }}}}$

La solució és que α és igual a 1.15, i al voltant del 9% de la riquesa és propietat de cadascun dels dos grups. Però de fet, el 69% de la població mundial adulta té només un 3% de la riquesa.^[30]

El coeficient de Gini mesura la desviació de la corba de Lorenz de la línia d'equidistribució que és una línea que connecta [0, 0] i [1, 1], que es mostra de color negre (α = ∞) en la gràfica de la corba de Lorenz de la dreta. En particular, el coeficient de Gini és dues vegades l'àrea entre la corba de Lorenz i la línea d'equidistribució. El coeficient de Gini de la distribució de Pareto és doncs calculat (per ${\displaystyle \alpha \geq 1}$) com

${\displaystyle G=1-2\left(\int _{0}^{1}L(F)\,dF\right)={\frac {1}{2\alpha -1}}}$

(vegeu Aaberge 2005).

Mètodes computacionals

Generació de mostres aleatòries

Es poden generar mostres aleatòries utilitzant el mètode de la transformada inversa. Donada una variable aleatòria U que segueix una distribució uniforme en l'interval unitari (0, 1], la variable T, definida com

${\displaystyle T={\frac {x_{\mathrm {m} }}{U^{1/\alpha }}}}$

segueix una distribució de Pareto.^[31] Si U està uniformement distribuïda en l'interval [0, 1), es pot intercanviar per (1 − U).

Referències

Bibliografia

• M. O. Lorenz «Methods of measuring the concentration of wealth». Publications of the American Statistical Association, 9, 70, 1905, pàg. 209–19. Bibcode: 1905PAmSA...9..209L. DOI: 10.2307/2276207. JSTOR: 2276207.
• Pareto, Vilfredo. Librairie Droz. Ecrits sur la courbe de la répartition de la richesse, 1965, p. 48. ISBN 9782600040211. 
• Pareto, Vilfredo «La legge della domanda». Giornale Degli Economisti, 10, 1895, p. 59–68.
• Pareto, Vilfredo. Cours d'économie politique, 1896. DOI 10.1177/000271629700900314. 

Vegeu també

• Llei de Bradford
• Efecte Mateu
• Òptim de Pareto
• Llei de Zipf

Enllaços externs

• Michiel Hazewinkel (ed.). Pareto distribution. Encyclopedia of Mathematics (en anglès). Springer, 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric W., «Pareto distribution» a MathWorld (en anglès).
• Aabergé, Rolf. [https://web.archive.org/web/20200420080507/http://www3.unisi.it/eventi/GiniLorenz05/25%20may%20paper/PAPER_Aaberge.pdf Arxivat 2020-04-20 a Wayback Machine. Gini's Nuclear Family], maig 2005. 

• (desembre 1997) "Self-Similarity in World Wide Web Traffic: Evidence and Possible Causes" a IEEE/ACM Transactions on Networking. 5: 835–846 [Consulta: 17 març 2021]  Arxivat 2016-03-04 a Wayback Machine.