Distribució normal

Distribució normal

Funció de densitat de probabilitat La corba vermella és la distribució normal estàndard
Funció de distribució de probabilitat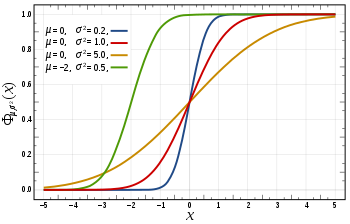
Tipus	distribution de Tweedie, Distribució t de Student, distribució normal multivariant, família exponencial, Distribució normal esbiaixada, Distribució estable, contaminated normal distribution (en) , distribució univariant i distribució de probabilitat contínua
Epònim	Carl Friedrich Gauß
Notació	${\displaystyle {\mathcal {N}}(\mu ,\,\sigma ^{2})}$
Paràmetres	μ ∈ R — mitjana (posició) σ² > 0 — variància (escala al quadrat)
Suport	${\displaystyle x\in \mathbb {R} }$
fdp	${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\,e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}$
FD	${\displaystyle {\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]}$
Quantil	${\displaystyle \mu +\sigma {\sqrt {2}}\,\operatorname {erf} ^{-1}(2F-1)}$
Esperança matemàtica	${\displaystyle \mu }$
Mediana	${\displaystyle \mu }$
Moda	${\displaystyle \mu }$
Variància	${\displaystyle \sigma ^{2}}$
Coeficient de simetria	${\displaystyle 0}$
Curtosi	${\displaystyle 0}$
Entropia	${\displaystyle {\frac {1}{2}}\ln(2\pi e\,\sigma ^{2})}$
FGM	${\displaystyle \mathrm {e} ^{\mu t+{\frac {\sigma ^{2}t^{2}}{2}}}}$
FC	${\displaystyle \mathrm {e} ^{\mathrm {i} \mu t-{\frac {\sigma ^{2}t^{2}}{2}}}}$
Informació de Fisher	${\displaystyle {\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}}$
Mathworld	NormalDistribution

La distribució normal, també coneguda com a distribució gaussiana, és una important família de distribucions de probabilitat contínues i és aplicable a molts camps. Cada membre de la família queda definit per dos paràmetres: la localització o mitjana ${\displaystyle \mu }$ i l'escala o desviació estàndard ${\displaystyle \sigma }$, i es denota per ${\displaystyle \ {\mathcal {N}}(\mu ,\sigma ^{2})}$. Un cas particular és la distribució normal estàndard, per la qual la mitjana és 0 i la desviació estàndard és 1. Fou Carl Friedrich Gauss qui descobrí la distribució normal quan analitzava dades astronòmiques, i definí l'equació de la seva funció de densitat de probabilitat.^[1] Aquesta distribució també s'anomena campana de Gauss, atès que el gràfic de la seva funció de densitat de probabilitat s'assembla a una campana.

La importància de la distribució normal en les ciències naturals i del comportament rau en el teorema central del límit. Aquest teorema estableix que la suma d'un elevat nombre d'efectes independents segueix (aproximadament) una distribució normal. D'aquesta manera, és útil en processos en els quals hi ha errors de mesura que es deuen a un elevat nombre de factors, tots ells contribuint una petita porció a l'error total. En la teoria de probabilitat i d'inferència estadística, el teorema central del límit garanteix que un llarg nombre d'estadístics segueixen la distribució normal, si més no aproximadament. Per exemple, la mitjana mostral o els estimadors màxim versemblants segueixen aproximadament una distribució normal sota certes condicions matemàtiques que són força generals.^[2]

Funció de densitat de probabilitat

${\displaystyle f(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}={\frac {1}{\sigma }}\,\phi \left({\frac {x-\mu }{\sigma }}\right)}$

on σ és la desviacio estàndard, μ és l'esperança matemàtica, i

${\displaystyle \phi (x)={\frac {1}{\sqrt {2\pi \,}}}\,e^{-{\frac {1}{2}}x^{2}}}$

és la funció de densitat de probabilitat de la distribució normal estàndard, és a dir, la distribució normal amb μ = 0 i σ = 1. Per comprovar que la integral de ${\displaystyle \varphi (x)}$ sobre la recta real és igual a 1 vegeu la integral de Gauß.^[3][4]

Funció de distribució

La funció de distribució d'una distribució normal ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$ és

Per a una distribució normal estàndard ${\displaystyle {\mathcal {N}}(0,1)}$ s'acostuma a utilitzar la notació ${\displaystyle \Phi (x)}$ per designar la seva funció de distribució. Concretament, Cal notar que

(Vegeu mes avall l'apartat sobre estandardització de variables normals).^[5][6]

Es important remarcar que la funció de distribució no és pot expressar en termes de funcions elementals (polinomis, exponencials, funcions trigonomètriques,..) Vegeu un comentari sobre la demostració d'aquesta propietat a l'article.^[7] Per aquest motiu, de cara a la utilització pràctica de les distribucions normals i els càlculs numèrics corresponents, les aproximacions a la funció de distribució són molt importants i s'han utilitzat tècniques d'integració numèrica, sèries de Taylor, sèries asimptòtiques o fraccions contínues. Vegeu Patel and Read per una revisió d'aquestes aproximacions.^[8]

Funcions generadores

Funció generadora de moments

La funció generadora de moments es defineix com a l'esperança matemàtica de exp(tX). Per la distribució normal la funció generadora de moments és:^[6]

$${\displaystyle M_{X}(t)=\mathrm {E} \left[\exp {(tX)}\right]=\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp {\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}\exp {(tx)}\,dx=\exp {\left(\mu t+{\frac {\sigma ^{2}t^{2}}{2}}\right)}.}$$

Funció característica

La funció característica es defineix com a l'esperança matemàtica de exp(itX), on i és el nombre imaginari, i t és un nombre real. Per la distribució normal la funció característica és:^[9][10]

$${\displaystyle \varphi _{X}(t)=E{\big [}e^{itX}]=\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\exp(itx)\,dx=\exp \left(i\mu t-{\frac {\sigma ^{2}t^{2}}{2}}\right).}$$

Propietats

Algunes propietats:

1. Si ${\displaystyle X\,\sim \,{\mathcal {N}}(\mu ,\sigma ^{2})}$ i ${\displaystyle a}$ i ${\displaystyle b}$ són nombres reals, aleshores ${\displaystyle aX+b\,\sim \,N(a\mu +b,(a\sigma )^{2})}$ (veure esperança i variància).^[11]
2. Si ${\displaystyle X\sim {\mathcal {N}}(\mu _{X},\sigma _{X}^{2})}$ i ${\displaystyle Y\sim {\mathcal {N}}(\mu _{Y},\sigma _{Y}^{2})}$ són variables aleatòries normals independents, aleshores:^[12][11]
   • La seva suma segueix la distribució normal amb ${\displaystyle U=X+Y\sim {\mathcal {N}}(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$.
   • La seva diferència segueix una distribució normal amb ${\displaystyle V=X-Y\sim {\mathcal {N}}(\mu _{X}-\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$.
   • ${\displaystyle U}$ i ${\displaystyle V}$ són independents si i només si ${\displaystyle \sigma _{X}=\sigma _{Y}}$.
   • La divergència de Kullback-Leibler,^[13] ${\displaystyle D_{\rm {KL}}(X\|Y)={1 \over 2}\left(\log \left({\sigma _{Y}^{2} \over \sigma _{X}^{2}}\right)+{\frac {\sigma _{X}^{2}}{\sigma _{Y}^{2}}}+{\frac {\left(\mu _{Y}-\mu _{X}\right)^{2}}{\sigma _{Y}^{2}}}-1\right).}$
3. Si ${\displaystyle X\sim {\mathcal {N}}(0,\sigma _{X}^{2})}$ i ${\displaystyle Y\sim {\mathcal {N}}(0,\sigma _{Y}^{2})}$ són variables aleatòries normals independents, aleshores:^[12]
   • El seu producte ${\displaystyle XY}$ segueix una distribució and funció de probabilitat de densitat ${\displaystyle p}$ donada per

     ${\displaystyle p(z)={\frac {1}{\pi \,\sigma _{X}\,\sigma _{Y}}}\;K_{0}\left({\frac {|z|}{\sigma _{X}\,\sigma _{Y}}}\right),}$ on ${\displaystyle K_{0}}$ és una funció de Bessel modificada de segon tipus.

   • El seu qüocient segueix una distribució de Cauchy amb ${\displaystyle X/Y\,\sim \,\mathrm {Cauchy} (0,\,\sigma _{X}/\sigma _{Y})}$.
4. Si ${\displaystyle X_{1},\dots ,X_{n}}$ són variables aleatòries independents idènticament distribuïdes amb distribució normal estàndard, aleshores ${\displaystyle X_{1}^{2}+\cdots +X_{n}^{2}}$ segueix una distribució khi quadrat amb n graus de llibertat.^[14]

Estandardització de variables aleatòries normals

Com a conseqüència de la propietat 1, és possible relacionar totes les variables aleatòries normals amb la distribució normal estàndard; aquest procediment s'anomena estandardització d'una variable normal.

Si ${\displaystyle \ X\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$, aleshores

${\displaystyle Z={\frac {X-\mu }{\sigma }}\!}$

és una variable aleatòria normal estàndard: ${\displaystyle \ Z\sim {\mathcal {N}}(0,1)}$. Una conseqüència important és que la funció de distribució de ${\displaystyle \ X}$ és :

${\displaystyle F(x;\mu ,\sigma )=\Pr(X\leq x)=\Phi \left({\frac {x-\mu }{\sigma }}\right),}$

on ${\displaystyle \Phi }$ és la funció de distribució normal estàndard: per a tot real t,

${\displaystyle \ \Phi (t)=\int _{-\infty }^{\,t}\phi (u)\,du=\int _{-\infty }^{\,t}{\frac {1}{\sqrt {2\,\pi }}}\,\mathrm {e} ^{-{\frac {u^{2}}{2}}}\,du={\frac {1}{2}}\left(1+\operatorname {erf} \left({\frac {t}{\sqrt {2}}}\right)\right).}$

D'altra banda, si ${\displaystyle Z}$ és una variable aleatòria normal estàndard, ${\displaystyle \ Z\sim {\mathcal {N}}(0,1)}$, aleshores

${\displaystyle X=\sigma \,Z+\mu }$

és una variable aleatòria normal amb esperança ${\displaystyle \mu }$ i variància ${\displaystyle \sigma ^{2}}$.

La funció de distribució normal estàndard ${\displaystyle \Phi }$ ha estat tabulada, i les altres funcions de distribució normals en són simples transformacions, tal com hem explicat anteriorment. Per tant, un pot emprar valors tabulats de la funció de distribució normal estàndard per a trobar el valor de la funció de distribució de qualsevol altra distribució normal.

Moments

Alguns dels primers moments de la distribució normal són:

Número	Moment	Moment central	Cumulant
0	1	1
1	${\displaystyle \mu }$	0	${\displaystyle \mu }$
2	${\displaystyle \mu ^{2}+\sigma ^{2}}$	${\displaystyle \sigma ^{2}}$	${\displaystyle \sigma ^{2}}$
3	${\displaystyle \mu ^{3}+3\mu \sigma ^{2}}$	0	0
4	${\displaystyle \mu ^{4}+6\mu ^{2}\sigma ^{2}+3\sigma ^{4}}$	${\displaystyle 3\sigma ^{4}}$	0

Tots els cumulants de la distribució normal a partir del segon són zero.

Moments d'una variable normal centrada

Per a les variables aleatòries normals centrades tenim la següent fórmula per als moments de qualsevol ordre. Si ${\displaystyle Z\sim {\mathcal {N}}(0,1)}$ aleshores ^[15]

Notem que on ${\displaystyle m!!}$ denota el doble factorial de ${\displaystyle m}$. Així, de forma més compacta podem escriure

Alternativament, usant la relació del doble factorial amb la funció gamma, per a ${\displaystyle k}$ parell,

on ${\displaystyle \Gamma (x)}$ és la funció gamma.

De la fórmula pels moments de ${\displaystyle Z}$ és dedueix que si ${\displaystyle X\sim {\mathcal {N}}(0,\sigma ^{2})}$, aleshores

Cas general

Sigui ${\displaystyle \ X\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$, i designem per ${\displaystyle m_{k}=E[X^{k}]}$ el moment d'ordre ${\displaystyle k}$ . Aleshores ^[16]

on ${\displaystyle [r]}$ designa la part entera del nombre ${\displaystyle r}$.

Recurrència pels moments d'una variable normal

Amb les notacions anteriors tenim ^[16]

Expressió compacta dels moments

Suposem que ${\displaystyle \sigma =1}$. Aleshores

on ${\displaystyle d^{n}f(x)/dx^{n}}$ designa la derivada d'ordre ${\displaystyle n}$-èssim de la funció ${\displaystyle f}$, amb el conveni ${\displaystyle d^{0}f(x)/dx^{0}=f(x)}$ . Aquesta fórmula és demostra mitjançant la regla de Leibniz per provar que la funció compleix la recurrència (*), amb ${\displaystyle P_{0}(\mu )=1}$ i ${\displaystyle P_{1}(\mu )=\mu }$.^[17]

Referències

Bibliogafia

• Bogaert, Patrick. Probabilités pour scientifiques et ingénieurs: Introduction au calcul des probabilités (en francès). De Boeck Superieur, juliol 2020. ISBN 978-2-8073-2655-2. 
• Cramer, Harald. Random Variables and Probability Distributions (en anglès). Cambridge University Press, 2013. 

Vegeu també

Viccionari

• Mètode dels mínims quadrats