Distribució t de Student

Distribució t de Student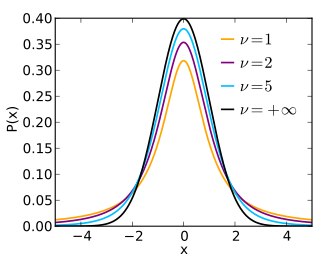

Funció de distribució de probabilitat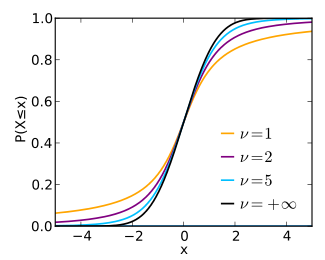
Tipus	Distribució t multivariant, Distribució t no central, família escala de localització, distribució de probabilitat simètrica, distribució univariant i distribució de probabilitat contínua
Epònim	William Gosset
Paràmetres	${\displaystyle \nu \in (0,\infty )}$ graus de llibertat
Suport	${\displaystyle x\in (-\infty ,\infty )}$
FD	${\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\times \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}}$ on ₂F1 és la funció hipergeomètrica
Esperança matemàtica	0 per a ${\displaystyle \nu >1}$
Mediana	0
Moda	0
Variància	${\displaystyle \textstyle {\frac {\nu }{\nu -2}}}$ per a ${\displaystyle \nu >2}$
Coeficient de simetria	0 per a ${\displaystyle \nu >3}$
Curtosi	${\displaystyle \textstyle {\frac {6}{\nu -4}}}$ per a ${\displaystyle \nu >4}$
Entropia	${\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi \left({\frac {1+\nu }{2}}\right)-\psi \left({\frac {\nu }{2}}\right)\right]\\[0.5em]+\ln {\left[{\sqrt {\nu }}B\left({\frac {\nu }{2}},{\frac {1}{2}}\right)\right]}\,{\scriptstyle {\text{(nats)}}}\end{matrix}}}$ on ψ és la funció digamma i B és la funció beta
FGM	cap valor
FC	${\displaystyle \textstyle {\frac {K_{\nu /2}\left({\sqrt {\nu }}|t|\right)\cdot \left({\sqrt {\nu }}|t|\right)^{\nu /2}}{\Gamma (\nu /2)2^{\nu /2-1}}}}$ on ${\displaystyle K_{\nu }(x)}$ és Funció de Bessel modificada de segon tipus
Mathworld	Studentst-Distribution

En probabilitat i estadística, la distribució t de Student és una distribució de probabilitat que sorgeix del problema d'estimar la mitjana d'una població normalment distribuïda amb variància desconeguda quan la mida de la mostra és petita. Aquesta és la base de la popular prova t de Student per a la determinació de les diferències entre dues mitjanes mostrals i per a la construcció de l'interval de confiança per a la diferència entre les mitjanes de dues poblacions.

El seu nom, Student, es deu al pseudònim que utilitzava l'estadístic britànic William Sealey Gosset quan publicava els seus articles científics. Per a la història d'aquesta distribució vegeu la pàgina Prova t de student. La referència bàsica d'aquest article és Johnson et al.^[1].

Definició

Sigui ${\displaystyle Z\sim {\mathcal {N}}(0,1)}$ una variable aleatòria normal estàndard i ${\displaystyle Q\sim \chi ^{2}(\nu )}$ una variable aleatòria amb distribució ${\displaystyle {\ce {\chi^2}}}$ amb ${\displaystyle \nu }$ graus de llibertat, ${\displaystyle Z}$ i ${\displaystyle Q}$ independents. La variable

es diu que té una distribució ${\displaystyle t}$ de Student amb ${\displaystyle \nu }$ graus de llibertat i s'escriu ${\displaystyle T\sim t(\nu )}$ o bé ${\displaystyle T\sim t_{\nu }}$.

Comentari sobre els graus de llibertat. El cas més habitual d'una distribució ${\displaystyle {\ce {\chi^2}}}$ és quan el nombre ${\displaystyle \nu }$ de graus de llibertat és un nombre natural i llavors es pot interpretar com la suma dels quadrats de ${\displaystyle \nu }$ variables aleatòries normals estàndard independents. Però mitjançant la funció de densitat es pot definir una distribució ${\displaystyle {\ce {\chi^2}}}$ que tingui com a graus de llibertat qualsevol nombre real estrictament positiu ${\displaystyle {\ce {\nu \in (0,\infty )}}}$, nombre que continua anomenat-se els graus de llibertat de la distribució.^[2] En conseqüència, pot definir-se la distribució ${\displaystyle t}$ de Student amb graus de llibertat qualsevol nombre ${\displaystyle {\ce {\nu \in (0,\infty )}}}$. Cal dir que el programari estadístic estàndard, per exemple, el llenguatge R, utilitza graus de llibertat fraccionaris en certs tests estadístics.

Funció de densitat

La funció de densitat de la distribució ${\displaystyle t}$ de Student amb ${\displaystyle \nu \in (0,\infty )}$ graus de llibertat és

$${\displaystyle f(x)={\frac {\Gamma {\big (}{\frac {\nu +1}{2}}{\big )}}{{\sqrt {\pi \nu }}\,\,\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}{\bigg (}1+{\frac {x^{2}}{\nu }}{\bigg )}^{-{\frac {\nu +1}{2}}},\quad x\in \mathbb {R} ,}$$

on ${\displaystyle \Gamma (x)}$ és la funció gamma.

Utilitzant la funció Beta ${\displaystyle {\text{B}}(x,y)}$ i que ${\displaystyle \Gamma {\big (}{\tfrac {1}{2}}{\big )}={\sqrt {\pi }}}$ també es pot escriure

Funció parella. Cal remarcar que aquesta funció és parella : ${\displaystyle f(-x)=f(x)}$; gràficament, és simètrica respecte l'eix d'ordenades. Aquesta propietat és important en els càlculs de probabilitats.

Quan ${\displaystyle \nu }$ és un nombre natural, la funció de densitat és simplifica. Concretament,per a ${\displaystyle \nu =1}$,

Llavors i per tant es tracta d'una distribució de Cauchy (centrada en l'origen). Per a ${\displaystyle \nu \geq 3}$ senar, la constant de la funció de densitat és on ${\displaystyle k!!}$ és el doble factorial del nombre ${\displaystyle k}$.

Per a ${\displaystyle \nu }$ parell,

(Cal recordar que ${\displaystyle 0!!}$=1).

Funció de distribució

Quan el nombre de graus de llibertat és un nombre natural, la funció de distribució es pot donar explícitament en termes de funcions elementals, amb una expressió que es complica a l'augmentar els graus de llibertat.

${\displaystyle \nu }$	Funció de densitat	Funció de distribució
1	${\displaystyle {\frac {1}{\pi (1+t^{2})}}}$	${\displaystyle {\frac {1}{2}}+{\frac {1}{\pi }}\arctan(t)}$
2	${\displaystyle {\frac {1}{2{\sqrt {2}}\left(1+{\frac {t^{2}}{2}}\right)^{3/2}}}}$	${\displaystyle {\frac {1}{2}}+{\frac {t}{2{\sqrt {2}}{\sqrt {1+{\frac {t^{2}}{2}}}}}}}$
3	${\displaystyle {\frac {2}{\pi {\sqrt {3}}\left(1+{\frac {t^{2}}{3}}\right)^{2}}}}$	${\displaystyle {\frac {1}{2}}+{\frac {1}{\pi }}{\left[{\frac {1}{\sqrt {3}}}{\frac {t}{1+{\frac {t^{2}}{3}}}}+\arctan \left({\frac {t}{\sqrt {3}}}\right)\right]}}$
4	${\displaystyle {\frac {3}{8\left(1+{\frac {t^{2}}{4}}\right)^{5/2}}}}$	${\displaystyle {\frac {1}{2}}+{\frac {3}{8}}{\frac {t}{\sqrt {1+{\frac {t^{2}}{4}}}}}{\left[1-{\frac {1}{12}}{\frac {t^{2}}{1+{\frac {t^{2}}{4}}}}\right]}}$
5	${\displaystyle {\frac {8}{3\pi {\sqrt {5}}\left(1+{\frac {t^{2}}{5}}\right)^{3}}}}$	${\displaystyle {\frac {1}{2}}+{\frac {1}{\pi }}{\left[{\frac {t}{{\sqrt {5}}\left(1+{\frac {t^{2}}{5}}\right)}}\left(1+{\frac {2}{3\left(1+{\frac {t^{2}}{5}}\right)}}\right)+\arctan \left({\frac {t}{\sqrt {5}}}\right)\right]}}$

Expressions alternatives de la funció de distribució

Per al cas general podem escriure la funció de distribució en termes de la funció beta incompleta^[4]:

on ${\displaystyle y(t)=\nu /(\nu +t^{2})}$ i ${\displaystyle I_{x}(a,b)}$ és la funció beta incompleta regularitzada.

Per a ${\displaystyle t<0}$, atès que la funció de densitat és parella, el càlcul de ${\displaystyle F(t)}$ és fa per arguments de simetria.

També, per a ${\displaystyle t^{2}<\nu }$, es pot escriure la funció de distribució en termes d'una funció hipergeomètrica^[5]

on ${\displaystyle {}_{2}\!F_{1}}$ és una funció hipergeomètrica.

Moments

Sigui ${\displaystyle n}$ un nombre natural. Aleshores

• Si ${\displaystyle 1\leq n<\nu }$, tenim que
  $${\displaystyle E[T^{n}]={\begin{cases}0,&{\text{si}}\ n\ {\text{és senar}},\\\\\nu ^{n/2}\,{\dfrac {\Gamma {\big (}{\frac {n+1}{2}}{\big )}\,\Gamma {\big (}{\frac {\nu -n}{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2}}{\big )}\Gamma {\big (}{\frac {\nu }{2}}{\big )}}},&{\text{si}}\ n\ {\text{és parell}}.\end{cases}}}$$

  
• Si ${\displaystyle n\geq \nu }$, llavors ${\displaystyle E{\big [}\vert T^{n}\vert {\big ]}=\infty }$, i en conseqüència el moment d'ordre ${\displaystyle n}$ no existeix.

En el cas ${\displaystyle n}$ parell, ${\displaystyle n<\nu }$, també tenim ^[5]

En particular, si ${\displaystyle \nu >1}$, llavors ${\displaystyle E[T]=0}$. Si ${\displaystyle \nu >2}$, llavors

Aproximació normal

Sigui ${\displaystyle T_{\nu }\sim t(\nu )}$, aleshores per a ${\displaystyle \nu }$ gran, ${\displaystyle T_{\nu }}$ és aproximadament normal estàndard ${\displaystyle {\mathcal {N}}(0,1)}$.^[6]

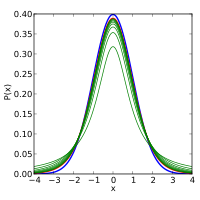
Els següents gràfics mostren la densitat de la distribució ${\displaystyle t_{\nu }}$ per a valors creixents de ${\displaystyle \nu }$. La densitat de la distribució normal estàndard està dibuixada en blau. Noteu que la densitat de la distribució ${\displaystyle t_{\nu }}$ (en vermell) s'aproxima cada com més a la normal quan ${\displaystyle \nu }$ creix.

Funció característica

Quan el nombre de graus de llibertat és una nombre natural, hi ha fórmules per la funció característica de la distribució de Student, que depenen de si els graus de llibertat son senars o parells, fórmules que cada cop són més complicades a l'augmentar el nombre de graus de llibertat^[7]. Una fórmula general utilitzant funcions especials va ser obtinguda el 1995 independentment per S. Hurst ^[8] i A. H. Jorder (veieu).^[9] Concretament, si ${\displaystyle T\sim t(\nu )}$,

on ${\displaystyle K_{\nu }(x)}$ és la funció de Bessel modificada de segon tipus.

La distribució t de Student amb tres paràmetres

La funció de densitat ${\displaystyle f}$ d'una distribució ${\displaystyle t(\nu )}$ permet construir de la manera habitual una família de posició i escala :^[10] sigui ${\displaystyle \mu \in \mathbb {R} }$ i ${\displaystyle \sigma >0}$  ; definim

Aquesta distribució s'anomena distribució ${\displaystyle t}$ de Student amb tres paràmetres, o distribució ${\displaystyle t}$ de Student amb posició i escala, i es designa per ${\displaystyle t(\nu ,\mu ,\sigma )}$ o ${\displaystyle t(\nu ,\mu ,\sigma ^{2})}$ . Alternativament, si ${\displaystyle X\sim t(\nu )}$ , llavors la variable aleatòria

té distribució ${\displaystyle t(\nu ,\mu ,\sigma )}$.

La distribució t de Student en Estadística

El paper central que té distribució ${\displaystyle t}$ de Student en la inferència estadística de poblacions normals és degut al següent teorema:^[11]

Teorema. Sigui ${\displaystyle X_{1},\dots ,X_{n}}$ una mostra d'una població normal ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$, és a dir, les variables aleatòries ${\displaystyle X_{1},\dots ,X_{n}}$ són independents i totes tenen distribució ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$. Considerem la mitjana mostral $${\displaystyle {\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}.}$$ Aleshores: ${\displaystyle {\frac {1}{\sigma ^{2}}}\sum _{i=1}^{n}{\big (}X_{i}-{\overline {X}}{\big )}^{2}\sim \chi ^{2}(n-1).}$ Les variables aleatòries ${\displaystyle {\overline {X}}}$ i ${\displaystyle \sum _{i=1}^{n}{\big (}X_{i}-{\overline {X}}{\big )}^{2}}$ són independents. Sigui $${\displaystyle T={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}},}$$ on $${\displaystyle S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}{\big (}X_{i}-{\overline {X}}{\big )}^{2},}$$ és la variància mostral. Llavors, ${\displaystyle T\sim t(n-1)}$.

Vegeu la pàgina de la distribució ${\displaystyle \chi ^{2}}$ per a la demostració dels punts 1 i 2. El punt 3 es dedueix del fet que ${\displaystyle {\overline {X}}\sim {\mathcal {N}}(\mu ,\sigma ^{2}/n)}$ i de les parts 1 i 2 i de la definició de la distribució ${\displaystyle t}$ de Student.

Vegeu la pàgina Interval de confiança per a exemples concrets d'utilització de la distribució de Student.

Relació amb altres distribucions

• La distribució ${\displaystyle t(1)}$ coincideix amb la distribució de Cauchy.
• Si ${\displaystyle T\sim t(\nu )}$, aleshores ${\displaystyle T^{2}}$ té una distribució ${\displaystyle F}$ amb 1 i ${\displaystyle \nu }$ graus de llibertat: ${\displaystyle T^{2}\sim F(1,\nu )}$ .

Vegeu també

• Prova t de Student
• Distribució ${\displaystyle \chi ^{2}}$
• Interval de confiança
• Distribució t no central

Notes

Bibliografia

• Johnson, N. L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 2. 2a edició. Nova York: Wiley, 1995. ISBN 0-471-58494-0.